Équation de Taylor-Goldstein

L'équation de Taylor–Goldstein est une équation différentielle ordinaire utilisée dans le domaine de la dynamique des fluides géophysiques, et plus généralement en dynamique des fluides, en présence de flux quasi bidimensionnel[1]. Elle décrit la dynamique de l'instabilité de Kelvin-Helmholtz assujettie à des forces de flottabilité, par exemple la gravité, de manière stable pour des fluides stratifiés dans la limite sans dissipation. Plus généralement elle s'applique à la dynamique des ondes internes (en) dans un écoulement cisaillé en présence d'un gradient vertical de vitesse. L'équation de Taylor-Goldstein est dérivée des équations d'Euler en deux dimensions, à l'aide de l'approximation de Boussinesq[2].

L'équation est nommée en l'honneur de G. I. Taylor[3] et S. Goldstein[4], qui ont indépendamment dérivé l'équation en 1931. La troisième dérivation indépendante, également en 1931, a été faite par B. Haurwitz[2].

Formulation

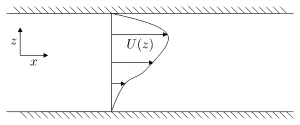
Un schéma de l'état de base du système. L'écoulement qui nous concerne est relatif à une petite perturbation de cet état. Tandis que l'état de base est parallèle, la vitesse de perturbation a des composantes dans les deux directions.

L'équation est obtenue par la résolution d'une version linéarisée de l'équation de Navier-Stokes, en présence de la gravité $g$ et une densité moyenne de gradient (de longueur $L_{\rho }$ ), pour le champ de vitesse de perturbation

\mathbf {u} =\left[U(z)+u'(x,z,t),0,w'(x,z,t)\right],\,

où $(U(z),0,0)$ est le débit de base non perturbé. La vitesse de perturbation a une solution ondulatoire $\mathbf {u} '\propto \exp(i\alpha (x-ct))$ , dont on prend la partie réelle. Grâce à cette connaissance, et la représentation en fonction de courant $u_{x}'=d{\tilde {\phi }}/dz,u_{z}'=-i\alpha {\tilde {\phi }}$ pour le débit, la forme tridimensionnelle de l'équation de Taylor-Goldstein est obtenue:

(U-c)^{2}\left({d^{2}{\tilde {\phi }} \over dz^{2}}-\alpha ^{2}{\tilde {\phi }}\right)+\left[N^{2}-(U-c){d^{2}U \over dz^{2}}\right]{\tilde {\phi }}=0,

où $N={\sqrt {g \over L_{\rho }}}$ est la fréquence de Brunt–Väisälä. La valeur propre du problème est $c$ . Si la partie imaginaire de la vitesse d'onde $c$ est positive, alors l'écoulement est instable, et la petite perturbation introduite dans le système est amplifiée avec le temps.

Notez qu'une fréquence $N$ de Brunt-Väisälä purement imaginaire résulte en un flux qui est toujours instable. Cette instabilité est connue sous le nom d'instabilité de Rayleigh-Taylor.

Conditions aux limites de non-glissement

Les conditions pertinentes aux limites sont, en cas de conditions de non-glissement en haut et en bas, $z=z_{1}$ et $z=z_{2}:$

\alpha {\tilde {\phi }}={d{\tilde {\phi }} \over dz}=0\quad {\text{ à }}z=z_{1}{\text{ et }}z=z_{2}.

Notes

(en) Pijush K. Kundu et Ira M. Cohen, Fluid Mechanics, Academic Press, 2002 (lire en ligne)
(en) Craik (1988, pp. 27–28).
(en) G. I. Taylor, « Effect of variation in density on the stability of superposed streams of Fluid », Proceedings of the Royal Society A,‎ 1931 (lire en ligne)
(en) S. Goldstein, « On the stability of superposed streams of Fluids of different densities », Proceedings of the Royal Society A,‎ 1931 (lire en ligne)

Références

(en) Craik, A.D.D. (1988), Wave interactions and fluid flows, Cambridge University Press, (ISBN 0-521-36829-4)

Portail de la physique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) Pijush K. Kundu et Ira M. Cohen, Fluid Mechanics, Academic Press, 2002 (lire en ligne)

[Craik_27_28-2] (en) Craik (1988, pp. 27–28).

[3] (en) G. I. Taylor, « Effect of variation in density on the stability of superposed streams of Fluid », Proceedings of the Royal Society A,‎ 1931 (lire en ligne)

[4] (en) S. Goldstein, « On the stability of superposed streams of Fluids of different densities », Proceedings of the Royal Society A,‎ 1931 (lire en ligne)