Flux non visqueux

Un flux non visqueux est l'écoulement d'un fluide non visqueux, c'est-à-dire dont la viscosité est nulle[1].

Il existe peu d'exemples de fluides non visqueux (aussi dénommés superfluides) mais ils ont de nombreuses applications en dynamique des fluides[2].

Spécificités

Le nombre de Reynolds d'un flux non visqueux approche de l'infini, puisque la viscosité est proche de zéro. Lorsque les forces visqueuses sont négligeables, comme dans le cas des flux non visqueux, l'équation de Navier-Stokes peut être simplifiée en une forme connue comme l'équation d'Euler. Cette équation simplifiée est applicable aux flux non visqueux ainsi qu'aux flux ayant une faible viscosité et un nombre de Reynolds beaucoup plus grand que 1. À l'aide de l'équation d'Euler, beaucoup de problèmes de dynamique des fluides impliquant une faible viscosité sont facilement résolus, cependant, le fait de supposer négligeable la viscosité n'est plus valide dans les régions proches d'une frontière solide[3],[4].

Superfluides
Hélium superfluide

L'état superfluide est l'état de la matière qui présente des écoulements sans frottement, à viscosité zéro, aussi connu comme flux non visqueux[2].

À ce jour, l'hélium est le seul fluide dont on ait découvert qu'il a la propriété de pouvoir être superfluide. Il le devient dès qu'il est refroidi en dessous de 2,2 K (ce point est connu sous le nom de point lambda[5] : à des températures au-dessus du point lambda, l'hélium existe sous forme liquide présentant un comportement normal de la dynamique des fluides. Une fois refroidi sous 2,2 K, il commence à montrer un comportement quantique. Par exemple, au point lambda, il présente une forte augmentation de la capacité thermique et s'il continue à être refroidi, cette capacité thermique diminue avec la température[6]. En outre, sa conductivité thermique est très grande. Ceci contribue aux excellentes propriétés de refroidissement de l'hélium liquide[7].

Applications

Les spectromètres utilisent un électroaimant qui pour être supraconducteur doit être extrêmement froid. Pour cela, cet électroaimant est plongé dans un réservoir d'hélium liquide, lui-même placé dans un vase Dewar (l'équivalent d'une bouteille Thermos) plein d'azote liquide. L'hélium comme liquide de refroidissement permet de minimiser le flux de fond dans des lectures dans l'infrarouge lointain. Certains spectromètres sont de conception simples, mais même à leur point le plus chaud, leur cadre est à moins de 20 kelvins. Ces appareils sont assez rares car l'hélium liquide est l'un des liquides de refroidissement les plus coûteux[8].

Grand collisionneur de hadrons.

L'hélium liquide a une très haute conductivité thermique, ce qui le rend très utile pour le refroidissement des supraconducteurs. Les supraconducteurs, tels que ceux utilisés au LHC (Large Hadron Collidor ou Grand collisionneur de hadrons) sont refroidis à des températures d'environ 1,9 K. Cette température permet aux électroaimants au niobium-titane d'atteindre un état supraconducteur. Sans l'utilisation de l'hélium superfluide, cette température ne serait pas possible. Refroidir à ces températures, avec ce fluide, est très onéreux et il en existe peu par rapport à d'autres systèmes de refroidissement[9].

Une autre application de l'hélium superfluide est son utilisation dans la compréhension de la mécanique quantique. L'usage de lasers pour regarder des petites gouttelettes permet aux scientifiques d'observer des comportements qui ne peuvent normalement pas être visibles. Cela est dû au fait que l'ensemble de l'hélium dans chaque gouttelette est dans le même état quantique. Cette application n'a pas d'utilisation pratique par elle-même, mais cela donne un point de vue pour mieux comprendre la mécanique quantique, ce qui aura plus tard des applications.

Nombre de Reynolds

Le nombre de Reynolds (Re) est une grandeur sans dimension, donc sans unité, qui est couramment utilisée en dynamique des fluides et en ingénierie[10],[11]. Décrit à l'origine par George Gabriel Stokes en 1850, il est devenu populaire grâce à Osborne Reynolds, d'après qui le concept a été spécialement nommé en 1908 par Arnold Sommerfeld[11],[12],[13]. Le nombre de Reynolds est calculé comme suit :

Symbole Description Unités
SI Standard
longueur caractéristique (en) m ft
vitesse du fluide m/s ft/s
Masse volumique du fluide kg/m^3 lb/ft^3
Viscosité cinématique du fluide m^2/s ft^2/s

En examinant les dimensions de chacun des paramètres, il devient évident que le nombre de Reynolds est sans unité. Sa valeur représente le rapport entre les forces d'inertie et les forces visqueuses dans un fluide, et elle est utile dans la détermination de l'importance relative de la viscosité[10]. Dans un flux non-visqueux, puisque les forces visqueuses sont à zéro, le nombre de Reynolds approche de l'infini[11]. Lorsque les forces visqueuses sont négligeables, le nombre de Reynolds est beaucoup plus grand que 1[11]. Dans de tels cas (Re >> 1), supposer qu'un flux est non-visqueux peut être utile en simplifiant beaucoup de problèmes de dynamique des fluides.

Les équations d'Euler
Un écoulement non-visqueux autour d'une aile

Dans une publication datant de 1757, Leonhard Euler décrit un ensemble d'équations régissant les flux non-visqueux[14]:

Symbole Description Unités
SI Standard
Dérivée matérielle
Opérateur Nabla
pression Pa psi
accélération due à la gravité m/s^2 ft/s^2

Supposer le flux non-visqueux, ou la viscosité négligeable, permet l'utilisation de l'équation d'Euler, et peut s'appliquer à de nombreux exemples de flux dans lequel les forces visqueuses sont insignifiantes[1]. Quelques exemples : l'écoulement autour d'une aile d'avion, le flux en amont autour des piliers d'un pont dans une rivière, et les courants océaniques[1].

Équations de Navier-Stokes

En 1845, George Gabriel Stokes publie un important ensemble d'équations, aujourd'hui connu comme les équations de Navier-Stokes[1],[15]. Claude-Louis Navier développe ces équations d'abord à l'aide de la théorie moléculaire, qui a été confirmée par Stokes en utilisant la théorie du continuum[1]. Les équations de Navier Stokes décrivent le mouvement des fluides[1]:

Lorsque le flux est non-visqueux, ou quand la viscosité peut être considérée comme négligeable, l'équation de Navier-Stokes se simplifie en l'équation d'Euler[1]. Cette simplification est beaucoup plus facile à résoudre, et peut s'appliquer à de nombreux types de flux dans lequel la viscosité est négligeable[1].

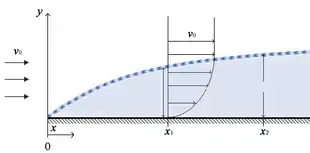
Flux en développement sur une surface solide.

Limites solides

Il est important de noter, que le caractère négligeable de la viscosité ne peut plus être assumé à proximité des limites solides, comme dans le cas de l'aile de l'avion[1]. Dans les régimes d'écoulement turbulent (Re >> 1), la viscosité peut généralement être négligée, cependant cela n'est valable qu'à une distance éloignée des interfaces solides[1]. Lors de l'examen des flux au voisinage d'une surface solide, comme le flux à travers un tuyau ou autour d'une aile, il est commode de classer les quatre régions distinctes de l'écoulement près de la surface[1]:

  • Flux turbulent principal : la plus éloignée de la surface, la viscosité peut être négligée.
  • Sous-couche d'inertie : le début du flux turbulent principal, la viscosité n'a qu'une importance mineure.
  • Couche tampon : la transformation entre la couche inertielle et la couche visqueuse.
  • Sous-couche visqueuse : plus proche de la surface, la viscosité est importante.

Bien que ces distinctions puissent être un outil utile pour illustrer l'importance des forces visqueuses près des interfaces solides, il est important de noter que ces régions sont assez arbitraires[1]. Supposer un flux non-visqueux peut être un outil utile dans la résolution de beaucoup de problèmes de dynamique des fluides, cependant, cette hypothèse nécessite un examen attentif des sous-couches fluides lorsque des frontières solides sont impliquées.

Voir aussi

Références
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Inviscid flow » (voir la liste des auteurs).
  1. (en) Warren E. Stewart et Edwin N. Lightfoot, Transport phenomena, Wiley, (ISBN 978-0-470-11539-8, OCLC 762715172, lire en ligne)
  2. (en) S., Stringari, Bose-Einstein condensation and superfluidity (ISBN 978-0-19-875888-4, OCLC 936040211, lire en ligne)
  3. Clancy, L.J., Aerodynamics, p.xviii
  4. Kundu, P.K., Cohen, I.M., & Hu, H.H., Fluid Mechanics, Chapter 10, sub-chapter 1
  5. (en) « This Month in Physics History », sur www.aps.org (consulté le )
  6. (en) L. Landau, « Theory of the Superfluidity of Helium II », Physical Review, vol. 60, no 4,‎ , p. 356–358 (DOI 10.1103/physrev.60.356, lire en ligne)
  7. (en) « nature physics portal - looking back - Going with the flow -- superfluidity observed », sur www.nature.com (consulté le )
  8. (en) J. R. Houck et Dennis Ward, « A liquid-helium-cooled grating spectrometer for far infrared astronomical observations », Publications of the Astronomical Society of the Pacific, vol. 91, no 539,‎ , p. 140–142 (lire en ligne)
  9. (en) « Cryogenics: Low temperatures, high performance | CERN », sur home.cern (consulté le )
  10. (en) Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera et David P. Dewitt,, Fundamentals of heat and mass transfer, Wiley, , 1048 p. (ISBN 978-0-470-50197-9, OCLC 875769912, lire en ligne)
  11. (en) N. Rott, « Note on the History of the Reynolds Number », Annual Review of Fluid Mechanics, vol. 22, no 1,‎ , p. 1–12 (DOI 10.1146/annurev.fl.22.010190.000245, lire en ligne)
  12. (en) Osborne Reynolds, « An Experimental Investigation of the Circumstances Which Determine Whether the Motion of Water Shall Be Direct or Sinuous, and of the Law of Resistance in Parallel Channels », Philosophical Transactions of the Royal Society of London, vol. 174,‎ , p. 935–982 (ISSN 0261-0523, DOI 10.1098/rstl.1883.0029, lire en ligne)
  13. (en) G. G. Stokes, « On the Effect of the Internal Friction of Fluids on the Motion of Pendulums », Transactions of the Cambridge Philosophical Society, vol. 9,‎ , p. 8 (lire en ligne)
  14. Leonhard Euler, « "Principes généraux de l'état d'équilibre d'un fluide" », Mémoires de l'académie des sciences de Berlin, vol. 11,‎ , p. 217–273 (lire en ligne)
  15. (en) G. G. Stokes, « On the Theories of the Internal Friction of Fluids in Motion and of the Equilibrium and Motion of Elastic Solids. », Proc. Cambridge Phil. Soc., vol. 8,‎ , p. 287–319
  • Portail de la physique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.