A5/1
A5/1 est un algorithme de chiffrement par flot utilisé dans le cadre des communications GSM. Il produit une suite pseudo-aléatoire avec laquelle on effectue un XOR avec les données. Une autre variante existe, la A5/2. On trouve aussi le terme de A5/3 (KASUMI), bien que ce dernier ne soit pas un algorithme de chiffrement par flot mais de bloc.
Pour les articles homonymes, voir A5.
L'algorithme A5 utilise une clé de 64 bits mais son implémentation dans le GSM n'utilise que 54 bits effectifs (10 bits sont mis à zéro).
Histoire
La version A5/1 est utilisée en Europe. La version A5/2 est plus vulnérable mais utilisée sur d'autres marchés, notamment en Amérique du Nord[réf. nécessaire]. En 1994, l'architecture du A5/1, à l'origine secrète, est publiée. En 1999, les versions 1 et 2 sont complètement spécifiées après de l'ingénierie inverse effectuée par Marc Briceno à partir d'un téléphone GSM. En 2000, on comptait environ 130 millions d'utilisateurs du GSM basé sur A5/1.
Principes
Une conversation GSM s'effectue par division en blocs temporels, chacun dure 4,6 millisecondes et contient 2×114 bits pour les deux canaux de communication (full-duplex). Une clé de session K est utilisée pour la communication. Pour chaque bloc, K est mélangée à un compteur de blocs et le résultat est utilisé comme état initial d'un générateur de nombres pseudo-aléatoires qui produit 228 bits. Ceux-ci servent au chiffrement après un XOR avec les données des deux canaux.
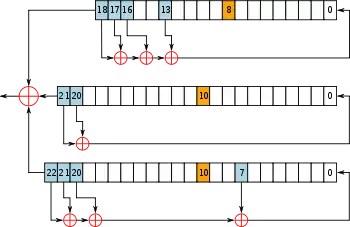
L'architecture de A5/1 est basée sur trois registres à décalage à rétroaction linéaire. Ils ont une longueur de 19, 22 et 23 bits. Pour insérer un nouveau bit dans le registre lors d'un décalage, on effectue pour chaque registre un XOR entre quelques bits déjà présents dans le registre. Les positions des bits utilisés sont constantes.
On récupère ensuite trois bits à des positions fixes, un par registre, avec lesquels on calcule une fonction « majorité » (le bit qui « gagne » est celui qui apparaît au moins deux fois). Les registres ayant produit le bit qui a emporté la majorité sont alors décalés. La véritable sortie du générateur est un XOR entre les bits qui sont en tête de chaque registre.
Pour initialiser le système avec la clé de 64 bits et le compteur initial de 22 bits, on procède comme suit :
- tous les registres sont mis à 0
- on effectue 64 cycles pendant lesquels la clé de 64 bits est introduite dans le système
- pour le bit Ki de la clé, on effectue un XOR avec le bit de poids faible de chaque registre
- on décale tous les registres d'un cran
- on effectue 22 cycles pendant lesquels le compteur de blocs (22 bits) est introduit dans le système
- pour le bit Ci du compteur, on effectue un XOR avec le bit de poids faible de chaque registre
- on décale tous les registres d'un cran
Attaques et vulnérabilités
Plusieurs attaques sur A5/1 ont été publiées. Certaines nécessitent un traitement préalable avec lequel on peut attaquer le chiffrement en quelques minutes.
Attaques à texte clair connu
En 1997, Golic présente une attaque basée sur la résolution d'un système d'équations linéaires. Son attaque a une complexité de 240.16 (nombre de solutions nécessaires pour résoudre le système).
En 2000, Alex Biryukov, Adi Shamir et David Wagner montrent que A5/1 peut être cryptanalysé en temps réel en utilisant une attaque avec un compromis temps-mémoire. Il est possible de retrouver la clé en quelques minutes à condition de disposer de deux minutes de communication en clair. Un calcul de 248 étapes est nécessaire alors pour préparer l'attaque (soit 300 Go de données).
La même année, Eli Biham et Orr Dunkelman publient une attaque avec une complexité de l'ordre de 239.91 itérations du générateur de nombres pseudo-aléatoires avec toutefois l'obligation de disposer de 220.8 bits de données non-chiffrées. L'attaque nécessite 32 Go et un précalcul de 238 opérations.
En 2003, Ekdahl et Johannson présentent une attaque sur l'initialisation de A5/1. En quelques minutes, il est possible de le casser en utilisant 5 minutes de conversation en clair. Avantage important, il n'est pas nécessaire de calculer une immense table au préalable. En 2004, Maximov et son équipe améliorent ce principe avec une minute de calcul et quelques secondes de conversation en clair.
En , le Chaos Computer Club annonce que le chiffrement du GSM aurait été cassé par Karsten Nohl qui devra faire la démonstration de sa technique en [1]. Si cette information est confirmée en , cette technique permettrait d'écouter les conversations chiffrées en A5/1.
Attaque sur des données chiffrées
En 2003, Barkan, Biham & Keller publient plusieurs attaques sur le système GSM. La première est active en forçant l'utilisation d'un chiffrement A5/2. Une fois cassé, le A5/2 fournit la clé qui est la même pour A5/1. Une autre attaque basée sur un compromis temps-mémoire est donnée et n'utilise pas de données en clair. Elle nécessite toutefois une grosse puissance pour précalculer la table.
Le , le Washington Post révèle que la NSA peut écouter les conversations téléphoniques de GSM, sur la base de documents fournis par Edward Snowden[2],[3].
Notes et références
- [PDF] Subverting the security base of GSM, Karsten Nohl et Sascha Krißler
- (en) Craig Timberg et Ashkan Soltani, « By cracking cellphone code, NSA has capacity for decoding private conversations », The Washington Post, (lire en ligne)
- Gilbert Kallenborn, « La NSA déchiffre toutes les communications GSM - Le service secret américain est capable d’aisément casser l’algorithme A5/1 pour intercepter les coups de fil passés en 2G. Du coup, certains opérateurs migrent leurs équipements vers son successeur A5/3, moins vulnérable », 01net.com, (lire en ligne)