Adimensionnement

Considérons un système simple caractérisé par deux variables : une variable dépendante ${\displaystyle x}$ et une variable indépendante ${\displaystyle t}$, où ${\displaystyle x}$ est une fonction de ${\displaystyle t}$. Les variables ${\displaystyle x}$ et ${\displaystyle t}$ représentent tous deux des quantités avec unité. Pour normaliser ces deux variables, supposons qu'il existe deux unités de mesure intrinsèques ${\displaystyle x_{c}}$ et ${\displaystyle t_{c}}$ dont les unités sont respectivement les mêmes que ${\displaystyle x}$ et ${\displaystyle t}$, telles que les conditions suivantes soient remplies :

${\displaystyle \tau ={\frac {t}{t_{c}}}\Rightarrow t=\tau t_{c}}$

${\displaystyle \chi (\tau )={\frac {x(t)}{x_{c}}}\Rightarrow x(t)=\chi (\tau )x_{c}.}$

Ces équations sont utilisées pour remplacer ${\displaystyle x}$ et ${\displaystyle t}$ lors de l'adimensionnement. Si des opérateurs différentiels sont nécessaires pour décrire le système original, leurs homologues normalisés deviennent des opérateurs différentiels sans dimension.

Bien que les noms destinés à remplacer x et t ne fassent l'objet d'aucune restriction, on les choisit généralement de telle sorte qu'ils paraissent commodes et intuitifs lors de leur utilisation dans le problème considéré. Par exemple, si x représente la masse, la lettre m pourrait être un symbole approprié pour représenter la quantité de masse sans dimension.

Dans cet article, les conventions suivantes sont utilisées :

• t représente la variable indépendante, habituellement une quantité de temps. Son homologue adimensionné est τ.
• x représente la variable dépendante, qui peut être une masse, une tension électrique ou toute autre quantité mesurable. Son homologue adimensionné est χ.

Un c souscrit ajouté au nom d'une variable associée à une quantité est utilisé pour indiquer l'unité caractéristique utilisée pour normaliser cette quantité. Par exemple, si x est une quantité, alors x_c est l'unité caractéristique utilisée pour la normaliser.

Considérons la relation

${\displaystyle \,\!t=\tau t_{c}\Rightarrow dt=t_{c}d\tau \Rightarrow {\frac {d\tau }{dt}}={\frac {1}{t_{c}}}.}$

L'expression des opérateurs différentiels sans dimension par rapport à la variable indépendante devient

${\displaystyle {\frac {d}{dt}}={\frac {d\tau }{dt}}{\frac {d}{d\tau }}={\frac {1}{t_{c}}}{\frac {d}{d\tau }}\Rightarrow {\frac {d^{n}}{dt^{n}}}=\left({\frac {d}{dt}}\right)^{n}=\left({\frac {1}{t_{c}}}{\frac {d}{d\tau }}\right)^{n}={\frac {1}{t_{c}^{n}}}{\frac {d^{n}}{d\tau ^{n}}}.}$

Si un système possède une fonction de forçage f(t), alors

${\displaystyle \,\!f(t)=f(\tau t_{c})=f(t(\tau ))=F(\tau ).}$

Ainsi, la nouvelle fonction de forçage F est rendue dépendante de la quantité sans dimension τ.

Considérons l'équation différentielle pour un système du premier ordre :

${\displaystyle a{\frac {dx}{dt}}+bx=Af(t).}$

La dérivation des unités caractéristiques donne

${\displaystyle t_{c}={\frac {a}{b}},\ x_{c}={\frac {A}{b}}.}$

Un système du second ordre est de la forme

${\displaystyle a{\frac {d^{2}x}{dt^{2}}}+b{\frac {dx}{dt}}+cx=Af(t).}$

Remplaçons les variables x et t par leurs homologues sans dimension. L'équation devient

${\displaystyle a{\frac {x_{c}}{t_{c}^{2}}}{\frac {d^{2}\chi }{d\tau ^{2}}}+b{\frac {x_{c}}{t_{c}}}{\frac {d\chi }{d\tau }}+cx_{c}\chi =Af(\tau t_{c})=AF(\tau ).}$

Cette nouvelle équation n'est pas sans dimension, bien que toutes les variables avec unités sont isolées dans les coefficients. En divisant par le coefficient du terme de plus grand ordre, l'équation devient

${\displaystyle {\frac {d^{2}\chi }{d\tau ^{2}}}+t_{c}{\frac {b}{a}}{\frac {d\chi }{d\tau }}+t_{c}^{2}{\frac {c}{a}}\chi ={\frac {At_{c}^{2}}{ax_{c}}}F(\tau ).}$

Il est ensuite nécessaire de déterminer les quantités de x_c et t_c de telle sorte que les coefficients deviennent normalisés. Comme il existe deux paramètres libres, on ne peut rendre égaux à un que deux coefficients au maximum.

Considérons la variable t_c :

1. Si ${\displaystyle t_{c}={\frac {a}{b}}}$, le terme du premier ordre est normalisé.
2. Si ${\displaystyle t_{c}={\sqrt {\frac {a}{c}}}}$, le terme d'ordre zéro est normalisé.

Les deux substitutions sont valides. Cependant, pour des raisons pédagogiques, la dernière substitution est utilisée pour les systèmes du second ordre. Choisir cette substitution permet à x_c d'être déterminé par la normalisation du coefficient de la fonction de forçage :

${\displaystyle 1={\frac {At_{c}^{2}}{ax_{c}}}={\frac {A}{cx_{c}}}\Rightarrow x_{c}={\frac {A}{c}}.}$

L'équation différentielle devient

${\displaystyle {\frac {d^{2}\chi }{d\tau ^{2}}}+{\frac {b}{\sqrt {ac}}}{\frac {d\chi }{d\tau }}+\chi =F(\tau ).}$

Le coefficient du terme du premier ordre est sans unité. Définissons

${\displaystyle 2\zeta \ {\stackrel {\mathrm {def} }{=}}\ {\frac {b}{\sqrt {ac}}}.}$

La présence du facteur 2 permet de paramétrer les solutions en fonction de ζ. Dans le contexte de systèmes mécaniques ou électriques, ζ est connu comme le taux d'amortissement, et est un paramètre important nécessaire à l'analyse des systèmes de contrôle. Le résultat de la définition est l'équation différentielle de l'oscillateur harmonique :

${\displaystyle {\frac {d^{2}\chi }{d\tau ^{2}}}+2\zeta {\frac {d\chi }{d\tau }}+\chi =F(\tau ).}$

L'équation différentielle linéaire d'ordre n à coefficients constants s'écrit, sous sa forme générale :

${\displaystyle a_{n}{\frac {d^{n}x(t)}{dt^{n}}}+a_{n-1}{\frac {d^{n-1}x(t)}{dt^{n-1}}}+\ldots +a_{1}{\frac {dx(t)}{dt}}+a_{0}x(t)=\sum _{k=0}^{n}a_{k}{\frac {d^{k}x(t)}{dt^{k}}}=Af(t).}$

La fonction f(t) est connue sous le nom de fonction de forçage.

Si l'équation différentielle contient uniquement des coefficients réels (aucun coefficient complexe), alors un tel système se comporte comme une combinaison de systèmes du premier et du deuxième ordre uniquement. Ceci est dû au fait que les racines de son polynôme caractéristique sont, soit réelles, soit des paires de complexes conjugués. Ainsi, comprendre comment l'adimensionnement s'applique aux systèmes du premier et du second ordre permet de déterminer les propriétés des systèmes d'ordre plus élevé par utilisation du principe de superposition.

Le nombre de paramètres libres dans une forme adimensionnée d'un système augmente avec son ordre. Pour cette raison, l'adimensionnement est rarement utilisé pour des équations différentielles d'ordre élevé. L'apparition du calcul formel a également réduit la nécessité de cette procédure.

Il est possible de représenter divers systèmes physiques de façon approchée au moyen de systèmes du premier ou du second ordre. C'est le cas notamment des systèmes mécaniques, électriques, fluides, thermiques et torsionnels. En effet, les quantités physiques fondamentales impliquées dans chacun de ces exemples sont liées par des dérivées du premier et du second ordre.

Une masse attachée à un ressort et à un amortisseur

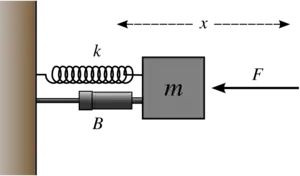
Supposons une masse attachée à un ressort et à un amortisseur, eux-mêmes attachées à un mur, et une force agissant sur la masse selon la même ligne.

Définissons :

• x = déplacement à partir de l'équilibre [m]
• t = temps [s]
• f = force externe ou « perturbation » appliquée au système [kg⋅m⋅s⁻²]
• m = masse du bloc [kg]
• B = constante d'amortissement de l'amortisseur [kg⋅s⁻¹]
• k = constante de force du ressort [kg⋅s⁻²]

Supposons que la force appliquée est une sinusoïde F = F₀ cos(ωt) ; l'équation différentielle qui décrit le mouvement du bloc est alors :

${\displaystyle m{\frac {d^{2}x}{dt^{2}}}+B{\frac {dx}{dt}}+kx=F_{0}\cos(\omega t)}$

L'adimensionnement de cette équation selon la méthode décrite dans la rubrique système du second ordre ci-dessus fournit plusieurs caractéristiques du système.

L'unité intrinsèque x_c correspond à la distance dont le bloc se déplace par unité de force

${\displaystyle x_{c}={\frac {F_{0}}{k}}.}$

La variable caractéristique t_c est égale à la période des oscillations

${\displaystyle t_{c}={\sqrt {\frac {m}{k}}}}$

et la variable sans dimension 2ζ correspond à la largeur de bande du système. ζ lui-même est le taux d'amortissement.

${\displaystyle 2\zeta ={\frac {B}{\sqrt {mk}}}}$

Pour un circuit RC série relié à une alimentation électrique

${\displaystyle R{\frac {dQ}{dt}}+{\frac {Q}{C}}=V(t)\Rightarrow {\frac {d\chi }{d\tau }}+\chi =F(\tau )}$

soit après substitutions

${\displaystyle Q=\chi x_{c},\ t=\tau t_{c},\ x_{c}=CV_{0},\ t_{c}=RC,\ F=V.}$

la première unité caractéristique correspond à la charge électrique totale dans le circuit. La seconde unité caractéristique correspond à la constante de temps du système.

Pour une configuration série de composants R, C, L où Q est la charge dans le système

${\displaystyle L{\frac {d^{2}Q}{dt^{2}}}+R{\frac {dQ}{dt}}+{\frac {Q}{C}}=V_{0}\cos(\omega t)\Rightarrow {\frac {d^{2}\chi }{d\tau ^{2}}}+2\zeta {\frac {d\chi }{d\tau }}+\chi =\cos(\Omega \tau )}$

soit après substitutions

${\displaystyle Q=\chi x_{c},\ t=\tau t_{c},\ \ x_{c}=CV_{0},\ t_{c}={\sqrt {LC}},\ 2\zeta =R{\sqrt {\frac {C}{L}}},\ \Omega =t_{c}\omega .}$

La première variable correspond à la charge maximum stockée dans le circuit. La fréquence de résonance est donnée par l'inverse du temps caractéristique. La dernière expression est la largeur de bande du système. Ω peut être considéré comme fréquence de la fonction de forçage normalisée.

L'équation de Schrödinger pour un oscillateur harmonique quantique à une dimension indépendant du temps est  :

${\displaystyle \left(-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}+{\frac {1}{2}}m\omega ^{2}x^{2}\right)\psi (x)=E\psi (x)}$ ;

C'est une équation différentielle linéaire, mais à coefficients non constants (en raison de la présence du terme ${\displaystyle x^{2}}$).

La fonction d'onde ψ elle-même représente une probabilité, qui est d'une certaine façon déjà sans dimension et normalisée. Il n'est donc pas nécessaire d'adimensionner la fonction d'onde. Cependant, elle doit être réécrite comme une fonction d'une variable sans dimension. En outre, la variable x a une unité de type longueur. Substituons alors :

${\displaystyle \chi ={\frac {x}{x_{c}}},\ \psi (x)=\psi (x(\chi ))=\psi (\chi ).}$

L'équation différentielle devient :

${\displaystyle \left(-{\frac {\hbar ^{2}}{2mx_{c}^{2}}}{\frac {d^{2}}{d\chi ^{2}}}+{\frac {m\omega ^{2}x_{c}^{2}}{2}}\chi ^{2}\right)\psi (\chi )=E\psi (\chi )\Rightarrow \left(-{\frac {d^{2}}{d\chi ^{2}}}+{\frac {m^{2}\omega ^{2}x_{c}^{4}}{\hbar ^{2}}}\chi ^{2}\right)\psi (\chi )={\frac {2Emx_{c}^{2}}{\hbar ^{2}}}\psi (\chi ).}$

Pour rendre le terme devant χ² sans dimension, posons :

${\displaystyle {\frac {m^{2}\omega ^{2}x_{c}^{4}}{\hbar ^{2}}}=1\Rightarrow x_{c}={\sqrt {\frac {\hbar }{m\omega }}}.}$

L'équation adimensionnée complète ainsi obtenue est :

${\displaystyle \left(-{\frac {d^{2}}{d\chi ^{2}}}+\chi ^{2}\right)\psi (\chi )={\frac {2E}{\hbar \omega }}\psi (\chi )\ {\stackrel {\mathrm {def} }{=}}\ {\mathcal {E}}\psi (\chi ).}$

Le facteur d'adimensionnement pour l'énergie est le même que celui de l'état fondamental de l'oscillateur harmonique. Habituellement, le terme correspondant à l'énergie n'est pas rendu sans dimension car l'un des objets principaux de la mécanique quantique est de déterminer les énergies des états d'un système. En réarrangeant la première équation, on met l'équation de l'oscillateur harmonique quantique sous une forme canonique :

${\displaystyle {\frac {\hbar \omega }{2}}\left(-{\frac {d^{2}}{d\chi ^{2}}}+\chi ^{2}\right)\psi (\chi )=E\psi (\chi )}$.

• Théorème de Buckingham
• Analyse dimensionnelle
• Grandeur sans dimension
• Système d'unités naturelles
• Équation différentielle
• Unité réduite

• (en) Mathematical Models in the Applied Sciences, Andrew Cadle Fowler, Cambridge University Press, 1997 (ISBN 978-0-521-46703-2) - chapitre Nondimensionalization (Extraits Google Books)

• (en) Analysis of differential equation models in biology: a case study for clover meristem populations, K. Louie, H. Clark, P.C.D. Newton, New Zealand Journal of Agricultural Research, 1998, Vol. 41: 567-576 (application de l'adimensionnement à un problème de biologie)
• (en) Course notes for Mathematical Modelling and Industrial Mathematics, Jonathan Evans, Department of Mathematical Sciences, University of Bath (voir le chapitre 3)