Algorithme de McNaughton et Yamada

En informatique théorique, et notamment en théorie des automates finis, l'algorithme de McNaughton et Yamada est un algorithme pour calculer une expression régulière à partir d'un automate fini. Elle porte le nom de Robert McNaughton et Hisao Yamada, deux scientifiques américain et japonais qui ont décrit l'algorithme[1]. Cet algorithme est également appelé algorithme de Kleene.

On appelle également algorithme de McNaughton et Yamada un autre algorithme, donné dans le même article[1], qui permet de construire un automate sans epsilon transitions à partir d'une expression régulière.

Principe

Étant donné un automate à n états, et dont les états sont numérotés de 1 à n, on donne une expression pour les langages composés des mots qui étiquettent les chemins de i à j, pour tout couple i, j. Cette expression est construite par récurrence au moyen d'une condition sur les chemins ; cette condition stipule que les chemins ne passent que par certains états autorisés. À chaque itération de l’algorithme, on fixe un nouvel état par lequel on s’autorise à passer. À la fin de l’algorithme, on obtient alors tous les chemins possibles.

Le fonctionnement de cet algorithme rappelle alors l’algorithme de Floyd-Warshall sur les graphes, où à chaque nouvelle étape, on s’autorise à passer par un nouveau sommet fixé.

Description

Soit ${\mathcal {A}}=(Q,{\mathcal {F}},I,T)$ un automate fini sur un alphabet $A$ , donné par un ensemble fini d'états $Q$ , un ensemble ${\mathcal {F}}\subset Q\times A\times Q$ de transitions, et des ensembles $I,T\subseteq Q$ d'états initiaux respectivement terminaux.

On note $L_{p,q}$ l'ensemble des mots qui sont étiquettes de chemins de $p$ à $q$ . Le langage $L$ reconnu par l'automate est l'ensemble

L=\bigcup _{i\in I}\bigcup _{t\in T}L_{i,t}

L'algorithme de McNaugthon et Yamada est une méthode pour calculer des expressions régulières pour les $L_{p,q}$ .

On note $L_{p,q}^{(k)}$ l'expression pour l’ensemble des mots qui étiquettent des chemins de $p$ à $q$ et dont tous les sommets intermédiaires sont inférieurs ou égaux à $k$ . Les sommets de départ $p$ et d’arrivée $q$ ne sont pas intermédiaires, donc ils ne sont pas soumis à la contrainte d’être inférieurs ou égaux à $k$ .

On construit les $L_{p,q}^{(k)}$ par récurrence sur $k$ , en commençant avec $k=0$ , et en terminant avec $k=n$ . Lorsque $k=n$ , la contrainte sur $k$ n’est plus une restriction, et $L_{p,q}^{(n)}=L_{p,q}$ si $p\neq q$ , et $\varepsilon +L_{p,p}^{(n)}=L_{p,p}$ .

Pour $k=0$ , comme les sommets sont numérotés à partir de 1, la contrainte exprime simplement qu’il n’y a pas de sommet intermédiaire. Les seuls chemins sont des transitions de $p$ à $q$ (on ignore un chemin de longueur 0 en un état $p$ ).

On a donc

L_{p,q}^{(0)}=\sum _{(p,a,q)\in {\mathcal {F}}}a

Pour la récurrence, on considère un chemin de $p$ à $q$ dont les sommets intermédiaires sont plus petits que $k$ . Deux cas sont alors possibles :

les sommets intermédiaires sont plus petits que $k-1$ ; alors l’étiquette est dans $L_{p,q}^{(k-1)}$ ;
le chemin passe par l’état $k$ . On décompose alors le chemin en parties dont les sommets intermédiaires sont plus petits que $k-1$ . Pour cela, on considère chaque occurrence du sommet $k$ dans ce chemin : entre deux occurrences consécutives, les sommets intermédiaires sont plus petits que k-1. On a alors la formule

L_{p,q}^{(k)}=L_{p,q}^{(k-1)}+L_{p,k}^{(k-1)}(L_{k,k}^{(k-1)})^{*}L_{k,q}^{(k-1)}

.

Il y a donc $n+1$ étapes ( $k=0,\ldots ,n$ ). Chacune des étapes demande le calcul de $n^{2}$ expressions, et la taille des expressions elles-mêmes croît avec $k$ . S’il est facilement programmable, l’algorithme est assez pénible à la main. Il est alors utile d’utiliser les règles qui permettent de simplifier des expressions régulières.

Pseudo-code

On va représenter les $L^{(k)}$ (respectivement $L$ ) sous forme de matrices, dont le coefficient en $(i,j)$ est $L_{i,j}^{(k)}$ (respectivement $L_{i,j}$ ). On a alors, pour ${\mathcal {A}}=(Q,{\mathcal {F}},I,T)$ un automate fini à $n$ états sur l'alphabet $A$ :

  Fonction McNaughton-Yamada( ${\mathcal {A}}$ )
      $L:=(\sum _{(p,a,q)\in {\mathcal {F}}}a)_{1\leq {\mathit {p}},{\mathit {q}}\leq n}$   \\à l'itération k de la boucle for, cette matrice représente  $L^{(k)}$ 
     for  ${\mathit {k}}:=1$  to  ${\mathit {n}}$ 
         for  ${\mathit {p}}:=1$  to  ${\mathit {n}}$ 
             for  ${\mathit {q}}:=1$  to  ${\mathit {n}}$ 
                 $L_{{\mathit {p}},{\mathit {q}}}:=L_{{\mathit {p}},{\mathit {q}}}+L_{{\mathit {p}},{\mathit {k}}}(L_{{\mathit {k}},{\mathit {k}}})^{*}L_{{\mathit {k}},{\mathit {q}}}$ 
     R :=  $\emptyset$   \\expression rationnelle à retourner
     for  ${\mathit {p}}\in I$ :
         for  ${\mathit {q}}\in T$ :
             if  ${\mathit {p}}=={\mathit {q}}$  then
                R := R +  $\varepsilon$  +  $L_{p,p}$  \\on n'ajoute  $\varepsilon$  qu'aux  $L_{p,p}$  où  ${\mathit {p}}\in I\cap T$ 
             else
                R := R +  $L_{p,q}$ 
     retourner R
  Fin Fonction

Exemples

Un premier exemple

L'automate

{\mathcal {A}}_{1}

considéré.

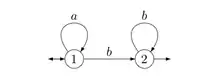
Appliquons l'algorithme de McNaughton et Yamada à l'automate ${\mathcal {A}}_{1}$ représenté. On va utiliser la représentation matricielle introduite dans la partie précédente. On a :

$L^{(0)}={\begin{pmatrix}a&b\\\emptyset &b\end{pmatrix}}$ ;
$L^{(1)}={\begin{pmatrix}a+a(a)^{*}a&b+a(a)^{*}b\\\emptyset &b+\emptyset (a)^{*}b\end{pmatrix}}={\begin{pmatrix}a^{+}&a^{*}b\\\emptyset &b\end{pmatrix}}$ ;
$L^{(2)}={\begin{pmatrix}a^{+}+(a^{*}b)(b)^{*}\emptyset &a^{*}b+(a^{*}b)(b)^{*}b\\\emptyset &b+bb^{*}b\end{pmatrix}}={\begin{pmatrix}a^{+}&a^{*}b^{+}\\\emptyset &b^{+}\end{pmatrix}}$ .

D'où $L={\begin{pmatrix}\epsilon +a^{+}&a^{*}b^{+}\\\emptyset &\epsilon +b^{+}\end{pmatrix}}={\begin{pmatrix}a^{*}&a^{*}b^{+}\\\emptyset &b^{*}\end{pmatrix}}$ .

Le langage $L({\mathcal {A}}_{1})$ reconnu par ${\mathcal {A}}_{1}$ est alors dénoté par l'expression rationnelle $L_{1,1}+L_{1,2}=a^{*}+a^{*}b^{+}$ . Après simplifications, on a $L({\mathcal {A}}_{1})=a^{*}b^{*}$ , ce qui est bien le résultat attendu.

L'automate

{\mathcal {A}}_{1}

, avec les états numérotés dans l'ordre inverse.

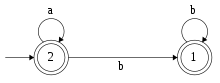
Considérons maintenant le même automate, mais avec une numérotation différente des états. L'algorithme appliqué à cet automate donne :

$L^{(0)}={\begin{pmatrix}b&\emptyset \\b&a\end{pmatrix}}$
$L^{(1)}={\begin{pmatrix}b^{+}&\emptyset \\b&a\end{pmatrix}}$
$L^{(2)}={\begin{pmatrix}b^{+}&\emptyset \\a^{*}b^{+}&a^{+}\end{pmatrix}}$

D'où

L={\begin{pmatrix}b^{*}&\emptyset \\a^{*}b^{+}&a^{*}\end{pmatrix}}

.

$L({\mathcal {A}}_{1})$ est alors dénoté par $L_{2,2}+L_{2,1}=a^{*}+a^{*}b^{+}$ , soit exactement la même expression rationnelle que précédemment : pour cet exemple particulier, le choix du nouvel état autorisé à chaque étape ne change pas l'expression rationnelle obtenue en fin d'algorithme.

Un deuxième exemple, où la numérotation des états change le résultat

L'automate

{\mathcal {A}}_{2}

.

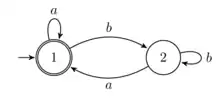
Donnons maintenant l'exemple présenté dans l'ouvrage de référence de Sakarovitch[2]. Appliquons maintenant l'algorithme à l'automate ${\mathcal {A}}_{2}$ . On a :

$L^{(0)}={\begin{pmatrix}a&b\\a&b\end{pmatrix}}$
$L^{(1)}={\begin{pmatrix}a^{+}&a^{*}b\\a^{+}&a^{*}b\end{pmatrix}}$
$L^{(2)}={\begin{pmatrix}(a^{*}b)^{*}a^{+}&(a^{*}b)^{+}\\(a^{*}b)^{*}a^{+}&(a^{*}b)^{+}\end{pmatrix}}$
$L={\begin{pmatrix}\varepsilon +(a^{*}b)^{*}a^{+}&(a^{*}b)^{+}\\(a^{*}b)^{*}a^{+}&(a^{*}b)^{*}\end{pmatrix}}$ .

D'où $L({\mathcal {A}}_{2})=L_{1,1}=\varepsilon +(a^{*}b)^{*}a^{+}$ .

L'automate

{\mathcal {A}}_{2}

, avec les états numérotés dans l'ordre inverse.

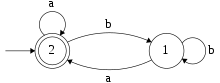
De même que pour le premier exemple, appliquons à nouveau l'algorithme en changeant la numérotation des états. On a :

$L^{(0)}={\begin{pmatrix}b&a\\b&a\end{pmatrix}}$
$L^{(1)}={\begin{pmatrix}b^{+}&b^{*}a\\b^{+}&b^{*}a\end{pmatrix}}$
$L^{(2)}={\begin{pmatrix}(b^{*}a)^{*}b^{+}&(b^{*}a)^{+}\\(b^{*}a)^{*}b^{+}&(b^{*}a)^{+}\end{pmatrix}}$
$L={\begin{pmatrix}(b^{*}a)^{*}b^{*}&(b^{*}a)^{+}\\(b^{*}a)^{*}b^{+}&(b^{*}a)^{*}\end{pmatrix}}$ .

D'où $L({\mathcal {A}}_{2})=L_{2,2}=(b^{*}a)^{*}$ : l'expression rationnelle obtenue pour le même langage est différente.

Notes et références

McNaughton et Yamada 1960.
(en) Jacques Sakarovitch, Elements of automata theory, Cambridge, Cambridge University Press, 1^er octobre 2009, 782 p. (ISBN 978-0-521-84425-3, BNF 42078268), p.96

Bibliographie

(en) Robert McNaughton et Hisao Yamada, « Regular expressions and state graphs for automata », IRE Trans. Electronic Computers, vol. EC-9, n^o 1,‎ janvier 1960, p. 39-47 (DOI 10.1109/TEC.1960.5221603).
(en) John E. Hopcroft, Rajeev Motwani et Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Pearson Addison Wesley, 2007, 3^e éd., xvii+535 (ISBN 978-0-321-45536-9 et 0201441241) — Section 3.2.1 From DFA’s to Regular Expressions, p. 93-98.
(en) Jacques Sakarovitch, Elements of automata theory, Cambridge University Press, 1^er octobre 2009, 782 p. (ISBN 978-0521844253), p. 96

Articles connexes

Portail de l'informatique théorique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[:0-1] McNaughton et Yamada 1960.

[2] (en) Jacques Sakarovitch, Elements of automata theory, Cambridge, Cambridge University Press, 1^er octobre 2009, 782 p. (ISBN 978-0-521-84425-3, BNF 42078268), p.96