Algorithme de Preparata-Hong
L'algorithme de Preparata-Hong est une méthode algorithmique pour calculer l'enveloppe convexe d'un ensemble fini de points dans l'espace euclidien de dimension 2 (le plan) ou de dimension 3 (l’espace). L'algorithme présente une stratégie utilisant le paradigme "diviser pour régner". Cet article présente uniquement le cas de la dimension 2.
Description du problème
On considère un ensemble fini de points. On suppose sans perte de généralité que tous les points ont toutes leurs coordonnées différentes. On cherche à trouver les sommets de son polygone convexe.
Principe en dimension 2
On commence par ranger les points de dans l'ordre croissant selon la dernière (i.e. deuxième) coordonnée. Notons le cardinal de . Soit l'ensemble après le tri.
Cas de base
Le cas de base dans l’algorithme diviser pour régner survient lorsqu’il y a 1, 2 ou 3 points. Dans ce cas, le calcul de l’enveloppe convexe est facile à calculer : il s'agit d'un point, d'un segment pour 2 points, d'un segment ou un triangle pour 3 points.
Cas récursif
S’il y a plus de 3 points, on commence par séparer l’ensemble des points en deux parties inférieure et supérieure de même cardinal à un point près, et on calcule leur enveloppe convexe respective par la stratégie diviser pour régner. On note et deux ensembles qui forment une partition de (on a pris pour la moitié plus éventuellement un des points de qui sont le plus "en bas" et le complémentaire de dans , c'est-à-dire la moitié moins éventuellement un des points de qui sont le plus "en haut"). On appelle enveloppe convexe inférieur l'enveloppe convexe de et enveloppe convexe supérieur l'enveloppe convexe de .
Ensuite, on vise à reconstruire l’enveloppe convexe globale à partir de ces enveloppes convexes inférieure et supérieure, en les reliant à la fois à gauche et à droite de la figure, par l’algorithme de fusion. À droite de la figure, on cherche à relier deux points provenant des parties inférieure et supérieure, en faisant en sorte que tous les points dans les deux parties soient à gauche de la droite tracée.
 Les enveloppes convexes supérieure et inférieure à fusionner.
Les enveloppes convexes supérieure et inférieure à fusionner.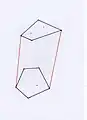 Jointure des enveloppes convexes.
Jointure des enveloppes convexes. L'enveloppe convexe finale fusionnée.
L'enveloppe convexe finale fusionnée.
On applique pour cela l’algorithme suivant (on appelle et les parties inférieure et supérieure respectivement) :
- On part des points les plus à droite de chaque partie, pour et pour ,
- On cherche dans tel que la pente de soit supérieure à la pente de ,
- On cherche dans tel que la pente de soit inférieure à la pente de ,
- On itère jusqu’à rencontrer un blocage.
À la fin de cet algorithme, on relie les deux points dans et que l’on a trouvés. On réalise la même opération à gauche de et , en adaptant l’algorithme ci-dessus, et on retire les arêtes superflues dans le nouveau polygone.
Algorithme de fusion dans le cas de la dimension 2
C'est l'algorithme que l'on va utiliser pour fusionner les enveloppes convexes supérieur et inférieur.
Soient et deux polygones convexes du plan euclidien.
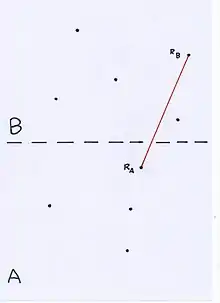
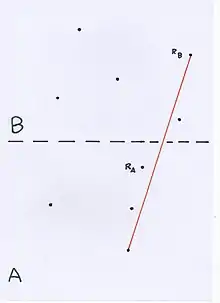
Soient des entiers strictement positifs, représentant respectivement le nombre de sommets de et de . Soient et les sommets en question. On suppose que les ordonnées des points du premier ensemble sont toutes strictement inférieures à celles des points du second ensemble. On suppose que dans la réunion de ces deux ensembles, les abscisses et les ordonnées sont distinctes deux-à-deux. Supposons aussi que dans chaque ensemble, on range les sommets dans le sens horaire de leur parcours sur le polygone à partir du sommet le plus "à droite" (celui d'abscisse la plus grande, il est représenté sur les figures ci-contre respectivement pour A et B par et ). À l'aide de l'algorithme précédent, on cherche à calculer l'enveloppe convexe de la réunion de ces deux ensembles de points, qu'on va noter , à partir de et . Pour des raisons pratiques, on pourra raisonner sur les indices des sommets de et respectivement modulo et modulo . Nous allons considérer que (le cas se traite de manière analogue, en ce qui concerne à la fois le pseudo-code et la correction).
Pour et , on note la pente de la droite . Pour on note la pente de la droite et pour on note la pente de la droite . On note et respectivement les indices du sommet de le plus "à gauche" (celui d'abscisse la plus petite) et du sommet de le plus "à gauche" (celui d'abscisse la plus petite).
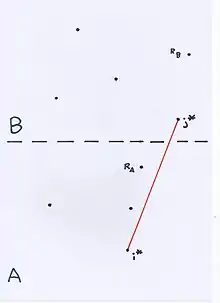
Le but de l'algorithme qui va suivre est de trouver la tangente droite de . Voici le pseudo-code de l'algorithme, on notera et respectivement l'abscisse et l'ordonnée de où est un point du plan euclidien, et on suppose que les coordonnées des sommets de et et que les valeurs pour et pour sont stockées dans des tableaux (accessibles à coût constant) :
Soient
On écrit
Si et faire et recommencer à partir de
Si et faire et recommencer à partir de
Renvoyer le couple
Il est facile de voir que l'algorithme termine car on incrémente et de 1 si on doit recommencer à partir de la deuxième ligne de pseudo-code et dans le cas marginal où et on passe directement à la dernière ligne de pseudo-code. De là, on remarque aussi que la complexité de l'algorithme est en , et donc en .
Correction de l'algorithme
Rechercher la tangente droite consiste à trouver les indices dans et dans telles que les points et soient ses extrémités. On se restreint au cas et .
Notons déjà quelques résultats qui s'obtiennent grâce à la convexité de et :
.png.webp)
- la suite est décroissante (voir la concaténation des segments associés comme une fonction convexe)
- la suite est décroissante (voir également la concaténation des segments associés comme une fonction convexe)
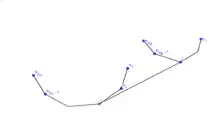
Ainsi, on peut caractériser géométriquement la pente de la tangente droite (de façon à ce qu'elle constitue bien un côté de l'enveloppe convexe issu de la fusion de et ) par :
- si , alors ;
- si , alors ;
- si , alors ;
- si , alors .
Il reste alors à montrer que l'algorithme renvoie bien ce que l'on souhaite, c'est-à-dire les indices dans et dans vérifiant la caractérisation ci-dessus.
On sait que l'algorithme s'arrête quand on a les deux conditions et . Pour être sûr que et , il faut s'assurer que l'on a l'intégralité de la caractérisation précédente. Pour cela, on distingue trois cas :
- soit on a , auquel cas on a directement la caractérisation, l'algorithme renvoie bien ce que l'on souhaite ;
- soit on a auquel cas soit la ligne 3 soit la ligne 4 n'est jamais exécutée, on peut alors montrer facilement que l'on a caractérisation en se penchant sur la seule ligne itérée ;
- soit il y a déjà eu une itération de la ligne 3 et la ligne 4 de pseudo-code, on distingue alors deux sous-cas :
l'indice est le dernier indice auquel on a fait une incrémentation, auquel cas on avait juste avant l'incrémentation, on a aussi (regarder le triangle sur la figure ci-contre) et par succession d'inégalités des pentes sur la chaîne , on réitère l'inégalité pour remonter à juste après la dernière incrémentation de l'indice (qui existe par hypothèse) et l'indice correspondant vérifie (car l'incrémentation de indique de et donc la chaîne est concave), par la chaîne d'inégalité on a bien , de même (par inégalité des pentes sur la fonction convexe issue de la chaîne ) cela donne : en incrémentant (de 1), on a finalement les conditions et ;
l'indice est le dernier indice auquel on a fait une incrémentation, juste avant cette incrémentation on a . De même on ne peut pas avoir , sinon on a la chaîne qui est concave, ce qui entraîne (inégalité des pentes) et comme la chaîne est concave par hypothèse, on obtient et donc que la chaine est concave , ce qui veut dire que ; si on revient sur le pseudo-code, si juste avant la dernière incrémentation de on avait une incrémentation de , alors on aurait eu d'après la troisième ligne de pseudo-code que , ce qui est impossible ; donc comme il est supposé qu'on a incrémenté au moins une fois, juste avant la dernière incrémentation de , on a encore une autre incrémentation de avec ; il s'obtient alors par récurrence qu'on ne va jamais atteindre dans l'exécution de l'algorithme : contradiction. On a alors la première inégalité . Aussi, comme la chaîne est concave par hypothèse, on obtient directement . Donc, en incrémentant (de 1), on a bien les conditions et .
Ceci termine la preuve de la correction de l'algorithme.
Complexité temporelle de l’algorithme
On suppose que pour un ensemble initial de points du plan, cet algorithme de fusion est exécuté en temps . Ainsi, en notant la complexité temporelle associée au calcul de l'enveloppe convexe de points du plan euclidien, stockés dans un tableau et triés par avance dans l'ordre croissant selon une coordonnée, on a la relation de récurrence suivante :
Par le master theorem ou par une analyse à la main, on conclut que est en . Comme le tri d'un tableau (par exemple par tri fusion) peut être réalisé en temps , la complexité totale de l'algorithme est elle aussi en .
Une autre approche du problème
Il existe une autre façon de calculer l'enveloppe convexe de en calculant deux convexes non bornés dont l'intersection des deux donne l'enveloppe convexe final, en déterminant pour chacun de ces convexes l'ensemble des segments et demi-droites qui les délimitent. Il s'agit d'une méthode proposée par F. Preparata et M. Shamos.
Liens externes
- Calcul d'enveloppe convexe - Gestion dynamique d'une enveloppe convexe (enseignement de l'informatique à l'école Polytechnique de France)
- Fonctions convexes : inégalité des pentes
Sources
- Article original de Preparata et Hong - Convex Hulls of Finite Sets of Points in Two and Three Dimensions[1]
- Calcul de complexité : le Master theorem - Algorithms[2] (Sanjoy Dasgupta, Christos H. Papadimitriou, Umesh V. Vazirani) ; Introduction to algorithms[3] (Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein)
- Calcul d'enveloppe convexe - Gestion dynamique d'une enveloppe convexe[4] (enseignement de l'informatique à l'école Polytechnique de France)
Notes et références
- (en) F. P. Preparata ; S. J. Hong, « Convex Hulls of Finite Sets of Points in Two and Three Dimensions »,
- (en) Sanjoy Dasgupta, Christos H. Papadimitriou, Umesh V. Vazirani, Algorithms, McGraw-Hill,
- (en) Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein, Introduction to algorithms, MIT press,
- Jean Berstel, « Gestion dynamique d'une enveloppe convexe »
- Portail des mathématiques