Analyse factorielle multiple

La troisième analyse de l’exemple introductif suppose implicitement un équilibre entre la flore et sol. Or, dans cet exemple, le simple fait que la flore soit représentée par 50 variables et le sol par 11 variables implique que l’ACP des 61 variables sera influencée majoritairement par la flore (au moins quant au premier axe). Ce n’est pas souhaitable.

Le cœur de l’AFM repose sur une analyse factorielle (ACP dans le cas de variables quantitatives, ACM dans le cas de variables qualitatives) dans laquelle les variables sont pondérées. Ces poids sont identiques pour les variables d’un même groupe (et varient d’un groupe à l’autre). Ils sont tels que l’inertie axiale maximum d’un groupe est égale à 1 : autrement dit, en faisant l’ACP (ou, le cas échéant, l’ACM) d’un seul groupe avec cette pondération, on obtient une première valeur propre égale à 1. Pour obtenir cette propriété, on affecte à chaque variable du groupe ${\displaystyle j}$ un poids égal à l’inverse de la première valeur propre de l’analyse (ACP ou ACM selon le type de variable) du groupe ${\displaystyle j}$.

Formellement, en notant ${\displaystyle \lambda _{1}^{j}}$ la première valeur propre de l’analyse factorielle du seul groupe ${\displaystyle j}$, l’AFM affecte le poids ${\displaystyle 1/\lambda _{1}^{j}}$ à chaque variable du groupe ${\displaystyle j}$.

Le fait d’équilibrer les inerties axiales maximum plutôt que les inerties totales (= le nombre de variables en ACP normée) confère à l’AFM plusieurs propriétés importantes pour l’utilisateur. De façon plus directe, son intérêt apparaît dans l’exemple suivant.

Soient deux groupes de variables définis sur le même ensemble d’individus.

1. Le groupe 1 est composé des deux variables non corrélées A et B.
2. Le groupe 2 est composé de deux variables {C1, C2} identiques à une même variable C peu corrélée aux deux premières.

Cet exemple n’est pas complètement irréaliste. On est souvent conduit à analyser simultanément des groupes multidimensionnels et unidimensionnels.

Chaque groupe, ayant le même nombre de variables, à la même inertie totale.

Dans cet exemple le premier axe de l’ACP est quasiment confondu avec C. En effet, il y a deux variables dans la direction de C : autrement dit, le groupe 2, ayant toute son inertie concentrée dans une direction, influence de façon prépondérante le premier axe. De son côté, le groupe 1, étant composé de deux variables orthogonales (= non corrélées), a son inertie équirépartie dans un plan (celui engendré par les deux variables) et ne pèse quasiment pas sur le premier axe.

Exemple numérique

Tableau 1. AFM. Données test. A et B (groupe 1) sont non corrélées. {C1, C2} (groupe 2) sont identiques. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C_{1}}$ ${\displaystyle C_{2}}$ ${\displaystyle 1}$ 1 1 1 1 ${\displaystyle 2}$ 2 3 4 4 ${\displaystyle 3}$ 3 5 2 2 ${\displaystyle 4}$ 4 5 2 2 ${\displaystyle 5}$ 5 3 4 4 ${\displaystyle 6}$ 6 1 2 2

Tableau 2. Données test. Décomposition de l'inertie dans l'ACP et l'AFM des données du tableau 1. ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$ ACP Inertie 2,14 (100 %) 1 dont groupe 1 0,24 (11 %) 1 dont groupe 2 1,91 (89 %) 0 AFM Inertie 1,28 (100 %) 1 dont groupe 1 0,64 (50 %) 1 dont groupe 2 0,64 (50 %) 0

Le tableau 2 regroupe les inerties des deux premiers axes de l’ACP et de l’AFM du tableau 1.

Les variables du groupe 2 contribuent à 88,95 % de l’inertie de l’axe 1 de l'ACP. Ce premier axe est presque confondu avec C : la corrélation entre C et ${\displaystyle F_{1}}$ vaut .976 ;

Le premier axe de l’AFM (du tableau 1) fait jouer un rôle équilibré aux deux groupes de variables : la contribution de chaque groupe à l’inertie de cet axe est rigoureusement égale à 50 %.

Le deuxième axe, quant à lui, ne dépend que du groupe 1. Ceci est naturel puisque ce groupe est bidimensionnel et que le second groupe, unidimensionnel, s’est exprimé sur le premier axe.

Introduire en actif plusieurs groupes de variables dans une analyse factorielle suppose implicitement un équilibre entre ces groupes.

Cet équilibre doit tenir compte du fait qu’un groupe multidimensionnel influence naturellement plus d’axes qu’un groupe unidimensionnel (qui ne peut être étroitement lié qu’à un seul axe).

La pondération de l’AFM, qui rend égale à 1 l’inertie axiale maximum de chaque groupe, joue ce rôle.

Le cœur de l’AFM étant une analyse factorielle pondérée, l’AFM fournit d’abord les résultats classiques de l’analyse factorielle.

1.Représentations des individus dans lesquelles deux individus sont d’autant plus proches qu’ils ont des valeurs voisines pour toutes les variables de tous les groupes ; en pratique, on se limite souvent au premier plan factoriel.

2.Représentations des variables quantitatives comme en ACP (cercle des corrélations).

Figure1. AFM. Données test. Représentation des individus sur le premier plan.

Figure2. AFM. Données test. Représentation des variables sur le premier plan.

Dans l’exemple :

• le premier axe oppose principalement les individus 1 et 5 (figure1).
• les quatre variables ont une coordonnée positive (figure 2) : le premier axe est un effet taille. De fait, l’individu 1 a de faibles valeurs pour toutes les variables et l’individu 5 à de fortes valeurs pour toutes les variables.

3. Indicateurs d’aide à l’interprétation : inerties projetées, contributions et qualité de représentation. Dans l’exemple, la contribution des individus 1 et 5 à l’inertie du premier axe vaut 45,7 % + 31,5 % = 77,2 % ce qui justifie de centrer l’interprétation sur ces deux points.

4. Représentations des modalités des variables qualitatives comme en ACM (une modalité est au barycentre des individus qui la possèdent). Pas de variables qualitatives dans l'exemple.

5. Représentations superposées des individus « vus » par chacun des groupes. Un individu considéré du point de vue d’un seul groupe est dit individu partiel (parallèlement, un individu considéré du point de vue de l’ensemble des variables est dit individu moyen car il est au barycentre de ses points partiels). Le nuage partiel ${\displaystyle N_{I}^{j}}$ rassemble les ${\displaystyle I}$ individus du point de vue du seul groupe ${\displaystyle j}$ (soit ${\displaystyle {i^{j},j=1,J}}$ ) : c’est le nuage analysé dans l’analyse factorielle (ACP ou ACM) séparée du groupe ${\displaystyle j}$. La représentation superposée des ${\displaystyle N_{I}^{j}}$ fournie par l’AFM est analogue, dans sa finalité, à celle fournie par l’analyse procustéenne.

Figure 3. AFM. Données test. Représentation superposée des nuages moyen et partiels.

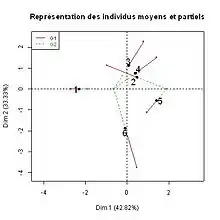
Dans l’exemple (figure 3), l’individu 1 est caractérisé par une petite taille (= petites valeurs) aussi bien du point de vue du groupe 1 que de celui du groupe 2 (les points partiels de l’individu 1 ont une coordonnée négative et sont proches). En revanche, l’individu 5 est plus caractérisé par des grandes valeurs pour les variables du groupe 2 que pour les variables du groupe 1 (pour l’individu 5, le point partiel du groupe 2 est plus éloigné de l’origine que celui du groupe 1). Cette interprétation faite à partir du graphique peut être validée directement dans les données.

6. Représentations des groupes de variables en tant que tels. Dans ces graphiques, chaque groupe de variables est représenté par un point. Deux groupes de variables sont d’autant plus proches qu’ils définissent la même structure sur les individus : à la limite, deux groupes de variables qui définissent des nuages d’individus ${\displaystyle N_{I}^{j}}$ homothétiques sont confondus. La coordonnée du groupe ${\displaystyle j}$ le long de l’axe ${\displaystyle s}$ est égale à la contribution du groupe ${\displaystyle j}$ à l’inertie du facteur de rang ${\displaystyle s}$ de l’AFM. Cette contribution peut s’interpréter comme un indicateur de liaison (entre le groupe ${\displaystyle j}$ et l’axe de rang ${\displaystyle s}$, d’où le nom de carré des liaisons donné à ce type de représentation). Cette représentation existe aussi dans d’autres méthodes factorielles (ACM et AFDM en particulier) auquel cas les groupes de variables sont réduits chacun à une seule variable.

Figure4. AFM. Données test. Représentation des groupes de variables.

Dans l’exemple (figure 4), cette représentation montre que le premier axe est lié aux deux groupes de variables alors que le deuxième axe n’est lié qu’au premier groupe. Ceci est bien en accord avec la représentation des variables (figure 2). En pratique, cette représentation est d’autant plus précieuse que les groupes sont nombreux et comportent beaucoup de variables.

Autre grille de lecture. Les deux groupes de variables ont en commun l’effet taille (premier axe) et diffèrent selon l’axe 2 puisque celui-ci est spécifique du groupe 1 (il oppose les variables A et B).

7. Représentations des facteurs des analyses séparées des différents groupes. Ces facteurs sont représentés comme des variables quantitatives supplémentaires (cercle des corrélations).

Figure 5. AFM. Données test. Représentation des composantes principales des ACP séparés des groupes.

Dans l’exemple (figure 5), le premier axe de l’AFM est assez fortement corrélé (r = .80) au premier axe du groupe 2. Ce groupe, étant constitué de deux variables identiques, ne comporte qu’une seule composante principale (confondue avec la variable). Le groupe 1 est constitué de deux variables orthogonales : toute direction du sous-espace engendré par ces deux variables présente la même inertie (égale à 1). Il y a donc indétermination dans le choix des composantes principales et il n’y a aucune raison de s’intéresser à l’une d’entre elles en particulier. Cela étant, les deux composantes fournies par le programme sont bien représentées : le plan de l’AFM est voisin du plan engendré par les deux variables du groupe 1.