Analyseur LR
Comme tout analyseur grammatical (ou analyseur syntaxique), un analyseur LR vise à vérifier si une chaîne de caractères (typiquement contenue dans un fichier) possède bien la structure d'une grammaire spécifiée à l'avance. Cette vérification s'accompagne généralement d'actions. Une action typique est la génération d'une autre chaîne de caractères ou encore d'un arbre d'analyse. Ainsi l'analyse grammaticale est généralement utilisée pour la compilation (transformation d'un code source en code machine). Sur le plan de l'informatique théorique, un analyseur LR (en anglais : Left to right, Rightmost derivation ) est un analyseur pour les grammaires non contextuelles qui lit l'entrée de gauche à droite (d'où le L de Left to right) et produit une dérivation droite (d'où la dénomination Rightmost qui signifie que les motifs spécifiés par la grammaire sont recherchés parmi les suffixes de la séquence de mots lue, donc sur la partie la plus à droite de cette séquence). Cette analyse a été inventée en 1965 par Donald Knuth (l'auteur du célèbre ouvrage: The art of programming). On parle aussi d'analyseur LR(k) où k représente le nombre de symboles « anticipés » (examinés dans la chaîne analysée sans être consommés) qui sont utilisés pour prendre des décisions d'analyse syntaxique. Comme usuellement k vaut 1, il est souvent omis. Une grammaire non contextuelle est appelée LR(k) s'il existe un analyseur syntaxique LR(k) pour elle.
On dit qu'un analyseur syntaxique LR réalise une analyse ascendante car il essaye de déduire les productions du niveau du haut de la grammaire en les construisant à partir des feuilles.
De nombreux langages de programmation sont décrits par des grammaires LR(1), ou du même genre, et, pour cette raison, les analyseurs syntaxiques LR sont souvent utilisés par les compilateurs pour faire l'analyse syntaxique de code source.
Typiquement, quand on se réfère à un analyseur syntaxique LR, on parle d'un analyseur syntaxique capable de reconnaître un langage particulier spécifié par une grammaire non contextuelle. Cependant, dans l'usage courant, on utilise le terme pour parler d'un programme pilote qui peut être appelé avec une certaine table et qui produit un large éventail d'analyseurs syntaxiques LR différents. On devrait plutôt appeler ces programmes générateurs d'analyseurs syntaxiques.
L'analyse syntaxique LR a plusieurs avantages :
- de nombreux langages de programmation peuvent être analysés en utilisant une variante d'analyseur syntaxique LR. Une exception notable est C++ ;
- les analyseurs syntaxiques LR peuvent être implémentés très efficacement ;
- de tous les analyseurs syntaxiques qui parcourent leur entrée de gauche à droite, les parseurs LR détectent les erreurs de syntaxe (c'est-à-dire quand les entrées ne sont pas conformes à la grammaire) le plus tôt possible.
Les analyseurs syntaxiques LR sont difficiles à produire à la main ; ils sont généralement construits par des générateurs d'analyse syntaxique ou des compilateurs de compilateurs. Suivant la manière dont la table d'analyse syntaxique est générée, ces analyseurs syntaxiques sont appelés analyseurs syntaxiques LR simples (SLR pour Simple LR parser), analyseurs syntaxiques LR avec anticipation (LALR pour Look-Ahead LR parser), et analyseurs syntaxiques canoniques. Ces types d'analyseurs syntaxiques peuvent traiter des ensembles de grammaires de plus en plus grands ; les analyseurs syntaxiques LALR peuvent traiter plus de grammaires que les SLR. Les analyseurs syntaxiques canoniques fonctionnent sur davantage de grammaires que les analyseurs syntaxiques LALR. Le très connu Yacc produit des analyseurs syntaxiques LALR.
Bien que la confusion soit fréquente, on ne doit pas confondre un analyseur LR avec un générateur d'analyseurs LR. Par exemple l'outil Yacc qui vient d'être cité n'est pas un analyseur LR à proprement parler mais bien un générateur d'analyseurs LR. Les deux notions se distinguent par leurs entrées-sorties. Un générateur d'analyseurs LR prend en entrée une grammaire et produit le code source de l'analyseur LR pour cette grammaire (et/ou des alertes/erreurs portant sur l’ambiguïté intrinsèque de la grammaire donnée en entrée). Tandis qu'un analyseur LR proprement dit prend en entrée une chaîne de caractères et produit en sortie un verdict (portant sur la conformité de cette chaîne à la grammaire ayant servi à produire cet analyseur) et éventuellement un produit de génération (un arbre d'analyse, une autre chaîne).
Architecture des analyseurs syntaxiques LR
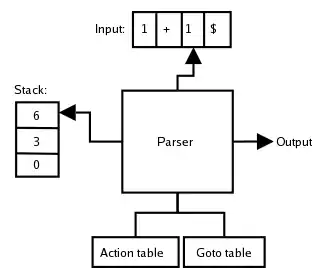
Conceptuellement, un analyseur syntaxique LR est un programme récursif qui peut être prouvé correct par calcul direct, et qui peut être implémenté efficacement par un analyseur syntaxique ascendant, lequel est un ensemble de fonctions mutuellement récursives, de la même manière qu'un analyseur syntaxique descendant. Cependant, par convention, les analyseurs syntaxiques LR sont présentés et implémentés par des machines à pile basées sur des tables, dans lesquelles la pile d'appels du programme récursif sous-jacent est manipulée explicitement.
Un analyseur syntaxique ascendant basé sur une table d'analyse syntaxique peut être représenté schématiquement par la figure 1. La suite montre une dérivation droite obtenue par cet analyseur syntaxique
Exemple Introductif
Pour expliquer comment procède un analyseur grammatical LR, nous utiliserons la petite grammaire constituées des règles (1) à (5) ci-dessous, en supposant que le symbole de départ est E. Pour rappel, dans des règles telles que ci-dessous, les majuscules désignent des symboles non terminaux ; les autres symboles (les minuscules, la ponctuation, les chiffres) désignent des symboles terminaux. Les symboles terminaux sont les unités syntaxiques insécables à partir desquelles le texte donné en entrée de l'analyseur est construit. Ces entités sont fournies à notre analyseur grammatical LR par un autre analyseur, dit analyseur lexical (que nous ne traitons pas ici) qui a pour fonction de découper le texte donné en entrée en une séquence de symboles terminaux. Le flot de traitement est donc le suivant: le texte donné en entrée est découpé en symboles terminaux par l'analyseur lexical (lexer en anglais) lequel envoie ces symboles à l'analyseur LR que nous nous proposons d'étudier. Pour simplifier la présentation nous supposerons que les symboles terminaux produits en sortie du lexer sont disponibles dans une mémoire tampon (dit buffer). Pour l'exemple ci-dessous les terminaux sont les symboles +, *, - , 0, 1. Au contraire des symboles terminaux, les symboles non terminaux dénotent des séquences de symboles (terminaux ou non). Ces séquences sont définies au travers de règles non contextuelles (comme les suivantes) qui, ensemble, forment une grammaire:
- (1) E → E * B
- (2) E → E + B
- (3) E → B
- (4) B → 0
- (5) B → 1
Les règles (4) (5) signifient que B peut être un 0 ou 1. La règle E → E + B signifie qu'un E peut être une séquence de la forme E + B. On peut noter le caractère récursif de cette règle. Le symbole E intervient dans sa propre définition. D'une façon générale il y a récursion quand un symbole non terminal est à la fois à gauche et à droite d'une règle. Une grammaire (un ensemble de règles) peut être donc être mal formée s'il y a circularité. Typiquement une règle E → E induit une circularité, ou bien par exemple E → F avec F → E. Dans notre exemple il n'y a pas circularité problématique car E peut être de la forme B et lui-même de la forme 0 ou 1, ce qui permet de sortir de la boucle.
Nous allons nous intéresser à savoir si l'entrée 1+1 est bien une instance de notre grammaire en utilisant une approche de type LR.
Pour procéder selon cette approche LR, d'abord nous ajoutons à la grammaire la règle (0) ci-dessous pour formaliser que le départ de la grammaire est E.
(0) ACCEPT → E$
On obtient ainsi une grammaire enrichie. Noter que les symboles ACCEPT et $ sont des symboles génériques (non spécifiques à notre grammaire). Le symbole $ est un symbole de fin de chaîne (pour les programmeurs: il s'agit du fameux EOF .. End Of File). Quant au symbole ACCEPT il est introduit de manière à pouvoir conclure de façon automatique le processus de reconnaissance. Dans la littérature, comme dans l'exposé du cas général plus bas, le symbole ACCEPT est souvent appelé S (pour Start).
La règle (0) permet donc à la fois de formaliser que E est le vrai symbole de départ et aussi de fonder le critère final d'acceptation qui est: à la fin de l'analyse la pile de l'analyseur doit ne contenir que ACCEPT et le buffer contenant la chaîne à analyser doit être vide (ceci sera illustré plus bas).
Finalement se demander si la chaîne 1+1 est une dérivation de la grammaire constituée des règles (1) à (5), avec E comme symbole de départ, revient à se demander si la chaîne 1+1$ est une dérivation de la grammaire enrichie constituée des règles (0) à (5) mais avec ACCEPT comme symbole de départ.
Donc notre analyseur LR utilise une pile (stack en anglais) qui obéit donc à une logique LIFO (Last In First Out). Il utilise aussi un buffer contenant les symboles terminaux de la chaîne à analyser. Au départ la pile de l'analyseur est vide et son buffer contient l'entrée à analyser soit ici:
1+1$
Le symbole le plus à gauche du buffer (d'où le L pour Left dans la dénomination LR) est retiré du buffer. Ici ce symbole est 1. Ce symbole est placé dans la pile. La tête de lecture du buffer se positionne sur le symbole suivant, donc sur le symbole +. La pile se présente ainsi (dans cette représentation de pile on suppose que les symboles entrent par le haut):
| [ 1 ] |
Comme à chaque étape, l'analyseur regarde la pile comme un motif M formé par la suite de symboles présents dans la pile en partant du bas de pile vers le haut. Il cherche si un suffixe s de ce motif M est identique à la partie droite d'une règle N → s de la grammaire. Si c'est le cas cela signifie que le symbole non terminal N a été reconnu. L'analyseur effectue alors cette action: il dépile les symboles formant le suffixe s puis il empile N à la place. Ainsi on aura remplacé dans la pile tous les symboles de s par l'unique symbole N. Cet aspect ressortira plus clairement ci-dessous quand la pile contiendra davantage de symboles. On peut remarquer que cette opération, appelée réduction, s'effectue sur le ou les symboles du sommet de pile, c'est-à-dire sur le ou les dernier(s) symboles lu(s) / reconnu(s) ; c'est-à-dire sur la partie la plus à droite de la chaîne qui est en train d'être analysée. C'est en cela que la dérivation se fait le plus à droite (d'où le R pour Rightmost dans la dénomination LR).
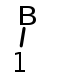
Pour l'instant on peut voir que le motif de pile M se résume au seul symbole 1 qui est exactement la partie droite de la règle (5). Ce symbole 1 peut donc être vu comme une dérivation de B selon la règle (5). L'analyseur remplace le 1 par B dans la pile (plus exactement il dépile 1, partie droite de (5) et empile B partie gauche de (5)). Cette opération effectuée par l'analyseur s'appelle une réduction. Elle produit l'arbre d'analyse ci-contre. La pile devient:
| [ B ] |
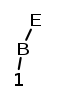
Le motif B, en tant que partie droite de la règle (3), est une dérivation de E par (3). L'analyseur effectue encore une réduction en dépilant B puis en empilant E ainsi que spécifié par la règle (3). L'arbre d'analyse est donné par la figure ci-contre. La pile devient:
| [ E ] |
Le motif de pile, constitué du seul symbole E, ne contient pas de suffixe matchant avec la partie droite d'une règle. Il n'y a donc pas de réduction possible. L'analyseur retire alors un nouveau caractère du buffer, soit le symbole + (sur lequel se tenait la tête de lecture). Cette tête de lecture passe au symbole suivant, qui est le deuxième et dernier 1. La pile devient:
| [ + ] |
| [ E ] |
Ici le motif de pile est E+. Aucun suffixe de ce motif ne correspond à la partie droite d'une règle. Donc aucune réduction n'est possible. Dès lors un nouveau symbole, le dernier 1, est retiré du buffer et est empilé dans la pile. La tête de lecture du buffer se positionne sur $, symbole de fin. La pile devient:
| [ 1 ] |
| [ + ] |
| [ E ] |
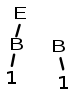
Ici le motif de pile est E+1. Le seul suffixe de ce motif correspondant à une partie droite est, comme plus haut le suffixe constitué du seul symbole 1. C'est la partie droite de (3). Ce 1 est remplacé par B selon la même réduction.
| [ B ] |
| [ + ] |
| [ E ] |
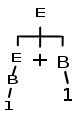
Ici le motif est E+B. Or E+B est lui-même un suffixe de E+B. En tant que suffixe E+B est identique à la partie droite de (2). Ce suffixe (donc le motif complet ) est dépilé. L'analyseur dépile donc 3 symboles. Il empile à la place E, symbole gauche de la règle (2). La pile devient:
| [ E ] |
Comme ci-dessus le motif de pile constitué du seul symbole E ne contient pas de suffixe matchant avec une partie droite de règle. Il n'y a donc pas de réduction possible. L'analyseur retire du buffer le dernier symbole, soit $. Le buffer est maintenant vide. La pile est dans l'état suivant:
| [ $ ] |
| [ E ] |
Le motif de pile est E$ qui est partie droite de la règle (0). L'analyseur réduit selon la règle (0):
| [ ACCEPT ] |
Ici la pile ne contient que le symbole d'acceptation ACCEPT ; par ailleurs le buffer est vide. Cette situation signifie que notre fichier 1+1$ est bien de la forme E$ et que donc vérifie la grammaire enrichie. De ce fait la chaîne 1+1 est bien une dérivation des règles de la grammaire initiale constituée des règles (1) à (5). L'analyseur s'arrête en notifiant l'acceptation de la chaîne donnée en entrée.
Dans le chapitre qui suit l'approche LR que l'on vient de décrire est formalisée avec un automate. Au lieu d'empiler les symboles, ce sont, de manière équivalente, des états d'un automate qui sont placés dans la pile.
Cas général
L'analyseur syntaxique est une machine à états. Elle consiste en :
- un tampon d'entrée ;
- une pile dans laquelle sont stockés des états (le calcul de ces états à partir de la grammaire est étudié plus loin) ;
- une table des branchements qui indique vers quel état elle doit aller ;
- une table des actions qui donne la règle de grammaire à appliquer en fonction de l'état courant et du terminal courant du flot d'entrée.
L'algorithme d'analyse syntaxique
L'algorithme d'analyse syntaxique LR fonctionne comme suit :
- la pile est initialisée avec l'état initial 0. Elle est donc de la forme [0]. L'état courant sera toujours l'état qui se trouve en haut de la pile (situé à droite dans les illustrations),
- en fonction de l'état courant et du terminal courant du flot d'entrée, une action est cherchée dans la table des actions. Quatre cas se présentent :
- cas 1, un décalage (shift) sn :
- le terminal courant est retiré du flot d'entrée,
- l'état n est mis sur la pile et devient l'état courant,
- cas 2, une réduction (reduce) rm :
- le nombre m est écrit dans le flot de sortie,
- pour chaque symbole de la partie droite de la règle numéro m, un état est retiré de la pile,
- en fonction de l'état qui est maintenant en haut de la pile et de la partie gauche de la règle m, un nouvel état est recherché dans la table des branchements, lequel est mis sur la pile et devient donc l'état courant,
- cas 3, une acceptation : la chaîne d'entrée est acceptée,
- cas 4, pas d'action : une erreur de syntaxe est rapportée ;
- cas 1, un décalage (shift) sn :
- l'étape 2 est répétée jusqu'à ce que la chaîne soit acceptée ou qu'une erreur de syntaxe soit rapportée.
Les tables des actions et des branchements
Les deux tables d'analyse syntaxique LR(0) de cette grammaire se présentent comme suit :
| états | actions | branchements | ||||||
| * | + | 0 | 1 | $ | E | B | ||
| 0 | s1 | s2 | 3 | 4 | ||||
| 1 | r4 | r4 | r4 | r4 | r4 | |||
| 2 | r5 | r5 | r5 | r5 | r5 | |||
| 3 | s5 | s6 | acc | |||||
| 4 | r3 | r3 | r3 | r3 | r3 | |||
| 5 | s1 | s2 | 7 | |||||
| 6 | s1 | s2 | 8 | |||||
| 7 | r1 | r1 | r1 | r1 | r1 | |||
| 8 | r2 | r2 | r2 | r2 | r2 | |||
La table des actions est indexée par l'état de l'analyseur syntaxique et par un terminal (dont le terminal spécial $ qui indique la fin du flot d'entrée). Elle contient trois types d'actions :
- décalage (shift), qui est écrite « sn » et qui indique que l'état suivant est n (et donc qu'il faut empiler n);
- reduction (reduce), qui est écrite « rm » et qui indique qu'il faut faire une réduction par la règle de grammaire numéro m ;
- acceptation, qui est écrite 'acc' et qui indique que l'analyseur syntaxique accepte la chaîne du flot d'entrée.
La table des branchements est indexée par l'état de l'analyseur syntaxique et par un non-terminal. Elle indique quel est l'état suivant de l'analyseur syntaxique s'il a effectivement reconnu ce non-terminal.
D'après la table ci-dessus, si on est dans l'état 0 et que le symbole courant du buffer est le symbole terminal 1 alors il faut effectuer un shift vers l'état 2 ce qui signifie que l'état 2 est empilé sur la pile des états (et ainsi devient l'état courant). Dans le même temps le buffer passe au symbole suivant.
D'après cette table si on est dans l'état 4 alors, quel que soit le symbole courant du buffer, il faut effectuer une réduction selon la règle 3 (qui est E → B). Cela signifie que les derniers symboles lus correspondent à la séquence à droite de cette règle (séquence se réduisant ici à B) et donc que l'on vient de reconnaître le symbole de gauche (ici E). On doit alors dépiler de la pile des états autant d'états que de symboles présents à droite de la règle (ici un seul puisqu'il n'y a que B), ce qui conduit à obtenir un nouveau sommet de pile s qui est brièvement l'état courant. Mais aussitôt l'analyseur doit considérer qu'il a reconnu le symbole de gauche de la règle, soit ici E. L'analyseur doit alors utiliser la table de branchement pour se positionner dans l'état indiqué à la ligne s et selon la colonne E de la table de branchement. Par exemple, si s est l'état 0, la table de branchement indique l'état 3 pour le couple (0,E). L'état 3 est alors aussitôt empilé et devient l'état courant (tout se passe comme si E avait été un symbole ajouté momentanément devant dans le buffer et aussitôt consommé).
Procédure d'analyse syntaxique
La table ci-dessous illustre chaque étape du processus pour l'analyse de l'expression: 1+1$. Dans cette table, l'état représente l'élément en haut de la pile (l'élément le plus à droite), et l'action suivante est déterminée en se référant à la table des actions/branchements ci-dessus. Un $ est ajouté au bout de la chaîne d'entrée pour indiquer la fin du flot.

| État | Flot d'entrée | Flot de sortie | Pile | Action suivante |
|---|---|---|---|---|
| 0 | 1+1$ | [0] | Décalage 2 | |
| 2 | +1$ | [0,2] | Réduction 5 | |
| 4 | +1$ | 5 | [0,4] | Réduction 3 |
| 3 | +1$ | 5,3 | [0,3] | Décalage 6 |
| 6 | 1$ | 5,3 | [0,3,6] | Décalage 2 |
| 2 | $ | 5,3 | [0,3,6,2] | Réduction 5 |
| 8 | $ | 5,3,5 | [0,3,6,8] | Réduction 2 |
| 3 | $ | 5,3,5,2 | [0,3] | Acceptation |
Description
Quand l'analyseur syntaxique démarre, il part toujours avec l'état 0 dans la pile :
- [0]
Le premier terminal que l'analyseur syntaxique voit est le '1'. D'après la table des actions, il doit aller à l'état 2. Ce qui donne pour la pile :
- [ 0 2 ]
Le haut de la pile, qui est l'état courant de l'analyseur, se trouve sur la droite, donc ici il s'agit de 2. Pour une meilleure compréhension adjoignons aux états de la pile, entre parenthèses et en italique, la partie de l'arbre de dérivation qui lui est attachée. Cela donne la notation suivante pour la même pile:
[ 0() 2(1) ]
Dans l'état 2, la table des actions dit que quel que soit le terminal suivant, dans le flot d'entrée, il faut faire une réduction par la règle de grammaire numéro 5. Cela signifie que l'analyseur syntaxique vient juste de reconnaître la partie droite de la règle numéro 5, ce qui est effectivement le cas.
Donc dans ce cas, nous écrivons 5 dans le flot de sortie, retirons un état de la pile. Le sommet de pile devient 0 et l'on vient de reconnaître un B. L'analyseur applique aussitôt la table de branchement. Pour le couple (0,B) celle-ci indique alors l'état 4. Cet état est empilé, comme si nous venions de lire un B depuis 0. La pile qui résulte de ces opérations est :
- [0() 4(B -1) ]
Dans l'état 4, la table des actions indique qu'il faut faire une réduction par la règle 3 (pour le suivi, le numéro de cette règle, 3, est produit sur le flot de sortie). L'analyseur enlève de la pile autant d'états que de symboles présents à droite de la règle de réduction. Donc ici un seul puisque la règle 3 n'a qu'un seul symbole à droite. Le nouveau sommet de pile devient temporairement l'état 0. L'analyseur utilise aussitôt la partie "branchements" de la table. Pour l'état 0 et le symbole E qui vient d'être reconnu, il est indiqué que l'état où se positionner est l'état 3. Cet état est empilé (comme pour un shift) et devient le nouvel état courant :
- [0() 3(E - B -1) ]
Le terminal suivant que l'analyseur syntaxique voit dans le flot d'entrée est un '+'. D'après la table des actions, il doit aller vers l'état 6 :
- [0() 3(E - B -1) 6(+) ]
La pile résultante peut être interprétée comme l'historique d'un automate fini qui vient juste de lire un non-terminal E suivi par un terminal '+'. La table de transition de cet automate est définie par les actions de décalages dans la table des actions ainsi que par les actions de branchements dans la table des branchements.
Le terminal suivant est maintenant '1'. Cela signifie que nous faisons un décalage et allons à l'état 2 :
- [0() 3(E - B -1) 6(+) 2(1) ]
Tout comme le '1' précédent, celui-ci est réduit vers B ; mais le branchement pour le couple (6,B) est 8 ; cet état est empilé, ce qui donne la pile suivante :
- [0() 3(E - B -1) 6(+) 8(B-1) ]
La pile correspond à une liste d'états d'un automate fini qui a lu un non-terminal E suivi d'un '+' et d'un non-terminal B. Dans l'état 8, nous faisons une réduction par la règle 2. Celle-ci comporte trois symboles à droite. On dépile les trois états du haut de la pile qui correspondent aux trois symboles de la partie droite de la règle 2. Le sommet de pile est temporairement 0. Aussi on vient de reconnaître la partie gauche de la règle 2, soit un E. La table de branchement pour le couple (0,E) indique l'état 3. Celui-ci est empilé, la pile devient:
[0() 3((E - B -1) + (B-1)) ]
Au bout du compte, le symbole '
Les numéros des règles qui ont été écrites sur le flot de sortie sont [5, 3, 5, 2] ce qui est effectivement une dérivation droite de la chaîne « 1 + 1 » à l'envers.
Construire des tables d'analyse syntaxique LR(0)
Items
La construction de ces tables d'analyse syntaxique est basée sur la notion d'items LR(0) (simplement appelés items ici) qui sont des règles de grammaire avec un point spécial ajouté quelque part dans la partie droite, ce point spécial représentant un état possible de l'analyseur (une situation courante possible). Par exemple, pour la règle E → E + B on peut avoir les quatre items (situations) suivantes :
- E → • E + B
- E → E • + B
- E → E + • B
- E → E + B •
Chaque item représente un état (une situation) de l'analyseur syntaxique. L'item E → E • + B, par exemple, indique que l'analyseur syntaxique a reconnu une chaîne correspondant à E sur le flot d'entrée, et qu'il s'attend à lire le symbole terminal + suivi d'une autre chaîne correspondant au non-terminal B.
Un item comme E → E + B • où le marqueur • est situé tout à droite de la partie droite de la règle, signifie que toute la partie droite a été reconnue comme une dérivation du symbole de gauche. Un tel item commande donc de faire une réduction.
Les règles de la forme A → ε ont un seul item A → •. En effet, puisque ε désigne une chaîne vide, il suit que •ε est équivalent à ε• qui est équivalent à •.
Ensemble d'items
Il n'est pas toujours possible de caractériser l'état courant de l'analyseur syntaxique avec un seul item. Dans notre exemple, après la lecture d'une chaîne correspondant à un E, il y a bien deux situations possibles représentées par les items: E → E • * B et E → E • + B.
Par conséquent, on caractérisera l'état de l'analyseur non par un seul item mais par un ensemble d'items.
Pour notre exemple, après avoir reconnu E, l'état courant est l'ensemble { E → E • + B, E → E • * B } qui indique que l'analyseur est en situation de lire le symbole + ou bien le symbole *.
Fermeture des ensembles d'items
Un item avec un point devant un non-terminal, tel que E → E + • B, indique que l'analyseur syntaxique s'attend à trouver ce non-terminal (en l'occurrence B, dans cet exemple). Pour s'assurer que l'ensemble d'items contient toutes les règles possibles, l'analyseur syntaxique doit inclure tous les items décrivant comment ce non-terminal B sera analysé. Cela signifie que s'il y a des règles telles que B → 0 et B → 1, l'ensemble d'items doit aussi inclure B → • 0 et B → • 1. De manière générale, cela peut être formulé ainsi :
- S'il y a un item de la forme A → v•Bw dans l'ensemble d'items, et s'il y a une règle de la forme B → w' alors l'item B → • w' doit également se trouver dans l'ensemble d'items.
Tous les ensembles d'items peuvent être étendus jusqu'à ce qu'ils satisfassent cette règle : continuer simplement d'ajouter les items appropriés jusqu'à ce que tous les non-terminaux précédés par des points soient pris en compte. En d'autres termes on ajoute des items jusqu'à atteindre un point fixe (tout ajout selon la règle ci-dessus laisse l'ensemble inchangé). L'extension minimale (le point fixe minimal) est appelée la fermeture d'un ensemble d'items et on l'écrira ferm(I) où I est un ensemble d'items. On verra plus bas qu'un état de l'analyseur syntaxique d'une grammaire est une fermeture d'items. Seules les fermetures accessibles depuis l'état initial (la fermeture initiale) seront considérées dans la table des actions et branchements. L'état initial est introduit par l'ajout d'une règle générique ainsi que décrit dans le chapitre qui suit.
La grammaire augmentée
Afin de disposer d'une fermeture initiale constituant l'état initial de l'analyseur, la grammaire est augmentée de la règle suivante :
- (0) S → E
où S est le nouveau symbole de départ et E l'ancien. L'analyseur syntaxique utilisera cette règle pour la réduction exactement quand il aura accepté la chaîne d'entrée.
Pour notre exemple, nous prendrons la même grammaire avec cette augmentation. Soit :
- (0) S → E
- (1) E → E * B
- (2) E → E + B
- (3) E → B
- (4) B → 0
- (5) B → 1
C'est avec cette grammaire augmentée que nous déterminerons les ensembles d'items et les transitions entre eux.
Trouver les ensembles d'items accessibles et les transitions entre eux
La première étape de la construction d'une table des actions et branchements consiste à déterminer les états (ensembles d'items fermés) ainsi que les transitions entre ces états de l'automate de l'analyseur. La méthode consiste à déterminer l'état initial de cet automate, puis à calculer de proche en proche tous les états accessibles. Les transitions sont déterminées comme si cet automate pouvait lire des terminaux et des non-terminaux.
État initial. L'état initial de cet automate est la fermeture du premier item de la règle ajoutée : S → • E :
- Ensemble d'items 0
- S → • E
- + E → • E * B
- + E → • E + B
- + E → • B
- + B → • 0
- + B → • 1
Le '+' devant les items indique ceux qui ont été ajoutés pour la fermeture. Les items originaux sans '+' sont appelés le noyau de l'ensemble d'items.
En partant de l'état initial (Ensemble d'items 0), on déterminera tous les états qui peuvent être atteints par une transition (successeurs). On obtient alors un nouvel ensemble d'états duquel on repart pour déterminer de nouveaux successeurs. Ceci est répété jusqu'à l'obtention d'un point fixe (qui est forcément atteint puisque le nombre de fermeture est fini). Détaillons le processus de calcul des transitions et des successeurs.
Calcul d'une transition de l'état successeur.
Les transitions possibles à partir d'un ensemble d'items Q peuvent être trouvées en regardant, dans cet ensemble d'items, les symboles (terminaux et non-terminaux) qui se trouvent juste après le point. S'il existe un tel symbole, disons x, pour trouver l'état (ensemble d'items) auquel conduit le symbole x à partir de l'état Q on procède comme suit :
- Prendre l'ensemble I de tous les items de Q où il y a un point juste à gauche de ce symbole x
- Créer l'ensemble I' en déplaçant, pour chaque item i de I, le point à droite du symbole x
- Ajouter l'ensemble I'' = ferm( I' ) comme état de l'automate
- Ajouter I – x → I'' comme transition de l'automate
Dans le cas de l'ensemble d'items 0, les symboles se trouvant juste après le point sont les terminaux '0' et '1' et les non-terminaux E et B. Les transitions qui en découlent sont les suivantes ...
Pour le terminal '0', la transition atteint l'état successeur:
- Ensemble d'items 1
- B → 0 •
et pour le terminal '1' :
- Ensemble d'items 2
- B → 1 •
Pour le non-terminal E :
- Ensemble d'items 3
- S → E •
- + E → E • * B
- + E → E • + B
et pour le non-terminal B :
- Ensemble d'items 4
- E → B •
La fermeture n'ajoute pas de nouveaux items dans tous les cas. On continue la procédure jusqu'à ce qu'aucun autre ensemble d'items puisse être trouvé. À partir des ensembles d'items 1, 2 et 4, il n'y aura pas de transitions puisque aucun point ne se trouve devant un symbole. En revanche pour l'ensemble d'items 3, on voit que le point se trouve devant les terminaux '*' et '+'. À partir de ensembles d'items 3 (ou état 3), pour le symbole '*', la transition conduit à l'état 5:
- Ensemble d'items 5
- E → E * • B
- + B → • 0
- + B → • 1
et pour '+' elle mène à l'état 6:
- Ensemble d'items 6
- E → E + • B
- + B → • 0
- + B → • 1
Pour l'ensemble d'items 5, on doit considérer les terminaux '0' et '1' et le non-terminal B. Pour les terminaux, on voit que les ensembles d'items fermés sont égaux respectivement aux ensembles d'items 1 et 2 déjà construits. Pour le non-terminal B, la transition donne :
- Ensemble d'items 7
- E → E * B •
Pour l'ensemble d'items 6, il faut également considérer les terminaux '0' et '1' et le non-terminal B. Comme précédemment, les ensembles d'items résultats pour les terminaux sont égaux aux ensembles d'items 1 et 2 déjà construits. Pour le non-terminal B, la transition conduit à :
- Ensemble d'items 8
- E → E + B •
Ces ensembles d'items 7 et 8 n'ont pas de symboles derrière leurs points et, donc, c'est fini, on a atteint un point fixe. La table de transitions pour l'automate ressemble maintenant à :
| Ensemble d'items | * | + | 0 | 1 | E | B |
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| 1 | ||||||
| 2 | ||||||
| 3 | 5 | 6 | ||||
| 4 | ||||||
| 5 | 1 | 2 | 7 | |||
| 6 | 1 | 2 | 8 | |||
| 7 | ||||||
| 8 | ||||||
Construire la table des actions et la table des branchements
À partir de cette table et de ces ensembles d'items, on construit la table des actions et la table des branchements de la manière suivante :
- les colonnes des non-terminaux sont copiées dans la table des branchements
- les colonnes des terminaux sont copiées dans la table des actions en tant qu'actions de décalage
- une colonne supplémentaire est ajoutée pour '
Le lecteur peut vérifier que cela donne effectivement la table des actions et la table des branchements qu'on a vues plus tôt.
Note au sujet de LR(0) par rapport à SLR et LALR
Seule l'étape 4 dans la procédure ci-dessus produit des actions de réduction, et donc toutes les actions de réductions occupent des lignes entières de la table, ce qui fait que les réductions arrivent indépendamment du symbole suivant du flot d'entrée. C'est la raison pour laquelle ce sont les tables d'analyse syntaxique LR(0) : elles ne font aucune anticipation (c'est-à-dire qu'elles ne regardent aucun symbole d'avance) pour décider quelle réduction faire.
Une grammaire qui a besoin d'anticipation pour désambiguïser les réductions aurait besoin de lignes de la table d'analyse syntaxique contenant différentes actions de réductions dans les différentes colonnes, et la procédure ci-dessus n'est pas capable de créer de telles lignes.
Des raffinements de la procédure de construction de la table LR(0) (tels que SLR et LALR) peuvent construire des actions de réductions qui n'occupent pas des lignes entières. Ils peuvent donc analyser plus de grammaires que les analyseurs syntaxiques LR(0).
Pour illustrer une telle ambiguïté considérons cette grammaire (enrichie) toute simple (le symbole S joue le rôle du ACCEPT de l'exemple introductif) :
- (0) S → A$
- (2) A → x
- (3) A → ε
qui vise à reconnaître la chaîne vide ε ou la chaîne se réduisant à x.
Sachant que dans un item •ε est équivalent à • l'état de départ de l'automate basé sur la clôture d'items est le suivant:
- S → • A$
- A → • x
- A → •
Le dernier item renvoie à une réduction puisque le marqueur est tout à droite d'une partie droite. De son côté le deuxième item indique que l'analyseur peut lire le symbole terminal x. Pour choisir entre ces deux possibilités l'analyseur a besoin d'anticipation. Pour une telle grammaire il s'agira d'examiner/consulter le contenu de la tête de lecture du buffer (sans le retirer du buffer). Si un état contient un item de la forme N → ω • (ou ω est un mot) et que la tête de lecture du buffer contient un symbole s qui fait partie des symboles terminaux qui peuvent suivre immédiatement N alors la réduction est effectuée. Sinon on effectue un shift. Ceci suppose de calculer au préalable les symboles suivants d'un non terminal. Ici Suivants(A) = {$} et d'après (0) on a: Suivants(S) = Suivants(A) = {$}.
Par exemple supposons qu'on fasse l'analyse de:
x$
Au départ la pile est vide, le buffer contient x$ et sa tête de lecture pointe sur x. On est dans l'état représenté par les 3 items ci-dessus. L'item A → • commande une réduction immédiate tandis que A → • x commande un shift par consommation de x. Mais x, symbole de la tête de lecture, n'appartient pas à Suivants(A) = {$} ce qui signifie que x n'est pas un symbole qui peut suivre une dérivation de A. Si on réduisait selon l'item A → • cela signifierait que x peut suivre A, en contradiction avec le fait que seul $ peut suivre A. Donc on ne peut réduire selon A → • et donc on applique le shift indiqué par l'item A → • x. Ainsi x est empilé et retiré du buffer. Le x est ensuite réduit en A. Puis le symbole $ est sortie du buffer et empilé. Le motif de pile A$ est réduit en S avec un buffer vide ce qui termine l'analyse.
Conflits dans les tables construites
L'automate est construit d'une manière telle qu'il n'est pas garanti d'être déterministe. Cependant, quand les actions de réductions sont ajoutées dans la table des actions, il peut arriver qu'une cellule contienne déjà une action de décalage (conflit décalage-réduction) ou une action de réduction (conflit réduction-réduction). Cependant, on peut prouver que cela n'arrive que dans les grammaires qui ne sont pas LR(0).
Conflit décalage/réduction
Un petit exemple d'une grammaire non-LR(0) avec un conflit décalage-réduction est :
- (1) E → 1 E
- (2) E → 1
Parmi les ensembles d'items, on trouve celui-ci :
- Ensemble d'items 1
- E → 1 • E
- E → 1 •
- E → • 1 E
- E → • 1
Il y a un conflit décalage/réduction car selon l'item E → 1 • , où le marqueur étant tout à droite, l'analyseur devrait faire une réduction (E a été reconnu). Mais par ailleurs selon l'item E → • 1 (ou bien E → • 1 E) l'analyseur devrait faire un décalage en consommant le terminal 1. On a donc un conflit décalage/réduction.
Conflit réduction/réduction
Un petit exemple d'une grammaire non-LR(0) avec un conflit réduction-réduction est :
- (1) E → A 1
- (2) E → B 2
- (3) A → 1
- (4) B → 1
Dans ce cas, on obtient l'ensemble d'items suivant :
- Ensemble d'items 1
- A → 1 •
- B → 1 •
Il y a un conflit réduction-réduction pour cet ensemble d'items parce que dans les cellules de la table des actions pour cet ensemble d'items, il y aurait en même temps une réduction par la règle 3 et une autre par la règle 4.
Résolution
Les deux exemples ci-dessus peuvent être résolus en permettant à l'analyseur syntaxique d'utiliser un ensemble de suites (voir l'analyse LL) d'un non-terminal A pour décider s'il va utiliser une des règles de A pour une réduction ; il n'utilisera la règle A → w pour une réduction que si le symbole qui suit dans le flot d'entrée est dans l'ensemble des suites de A. Cette solution conduit à ce qu'on appelle l'analyse SLR (analyse LR simple).
Références
- Compilateurs : principes, techniques et outils, Alfred V. Aho, Ravi Sethi et Jeffrey D. Ullman.
- Portail de l’informatique