Angle dièdre
En géométrie, l'angle entre deux plans est appelé angle dièdre, ou angle diédral (anglicisme).
Pour les articles homonymes, voir Dièdre.
L'angle dièdre d'un tétraèdre régulier, correspond à l'angle observé au sol, dans un plan perpendiculaire à l'une des arêtes au sol, que font la base du tétraèdre et une face. Face dont la base est, au sol, « vue de bout » (soit un point pour une arête).
L'angle dièdre de deux plans peut être mesuré sur les « bords » des plans, c'est-à-dire, suivant leur ligne d'intersection.
L'angle dièdre entre deux plans dénotés A et B est l'angle entre leurs deux vecteurs normaux et
Un angle dièdre peut être signé ; par exemple, l'angle dièdre peut être défini comme l'angle de rotation (suivant leur ligne d'intersection) qui permettrait au plan A pour se superposer au plan B. Donc, . En particulier, il suffit de spécifier cet angle ou son angle supplémentaire.
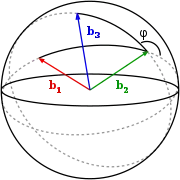 Figure 1 : Angle dièdre entre 3 vecteurs, défini comme l'angle extérieur sphérique. Plus les segments d'arc noirs sont longs, plus grands sont les grands cercles qui passent par et et par et , respectivement
Figure 1 : Angle dièdre entre 3 vecteurs, défini comme l'angle extérieur sphérique. Plus les segments d'arc noirs sont longs, plus grands sont les grands cercles qui passent par et et par et , respectivement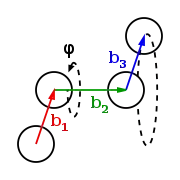 Figure 2 : Angle dièdre entre trois vecteurs consécutifs (représentés en rouge, vert, et bleu) connectant quatre atomes
Figure 2 : Angle dièdre entre trois vecteurs consécutifs (représentés en rouge, vert, et bleu) connectant quatre atomes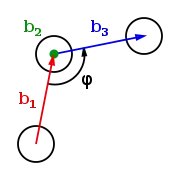 Figure 3 : Angle dièdre défini par trois vecteurs consécutifs (représentés en rouge, vert, et bleu) connectant quatre atomes. Depuis cette perspective, le second vecteur (en vert) sort de la page
Figure 3 : Angle dièdre défini par trois vecteurs consécutifs (représentés en rouge, vert, et bleu) connectant quatre atomes. Depuis cette perspective, le second vecteur (en vert) sort de la page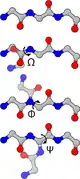 Figure 4 : Angle dièdre de l'ossature d'une protéine
Figure 4 : Angle dièdre de l'ossature d'une protéine
Référence
- Portail de la géométrie