Apside

Dans le cas d'une étoile et des principaux objets du système solaire, un terme spécialisé apparenté peut être employé comme indiqué dans le tableau ci-dessous. Le nom de ces points de plus petit et plus grand éloignement dépendent du corps central ; ils sont formés en prenant la racine grecque du nom de ce corps[1], qui est en général le nom d'un dieu.

Toutefois, seuls les couples périhélie et aphélie, périgée et apogée, périastre et apoastre sont couramment utilisés.

Les termes périlune ou apolune (pour le satellite naturel d'une lune), périjove ou apojove (pour un satellite de Jupiter) sont à éviter.

On voit parfois aussi les termes péricynthe ou apocynthe dans le cas d'un satellite artificiel de la Lune.

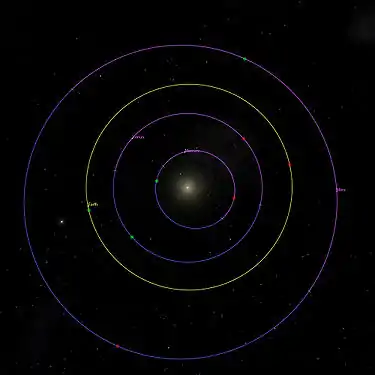
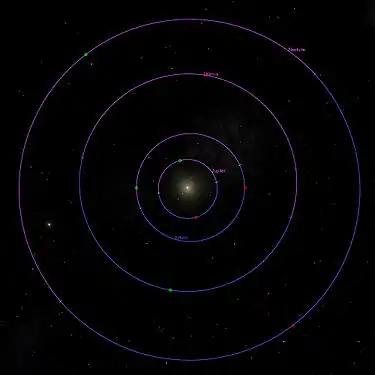
Les deux images ci-dessous montrent la position relative des périapsides (en vert) et apoapsides (en rouge) des planètes du système solaire, à notre époque.
Celle de gauche pour les planètes les plus intérieures, et celle de droite pour les planètes les plus extérieures.

Position relative des périapsides (en vert) et apoapsides (en rouge) des planètes les plus intérieures du système solaire.

Position relative des périapsides (en vert) et apoapsides (en rouge) des planètes les plus extérieures du système solaire.

Les formules suivantes permettent de calculer la distance de chacun des apsides au centre de masse, et la vitesse en ces points :

	périapside	apoapside
distance	${\displaystyle r_{\mathrm {per} }=(1-e)a\!\,}$	${\displaystyle r_{\mathrm {ap} }=(1+e)a\!\,}$
vitesse	${\displaystyle v_{\mathrm {per} }={\sqrt {\tfrac {(1+e)\mu }{(1-e)a}}}\,}$	${\displaystyle v_{\mathrm {ap} }={\sqrt {\tfrac {(1-e)\mu }{(1+e)a}}}\,}$

Selon les lois de Kepler sur le mouvement des planètes (conservation du moment angulaire) et les principes de la conservation de l'énergie, les quantités suivantes sont constantes pour une orbite donnée :

• moment angulaire relatif spécifique : ${\displaystyle h={\sqrt {(1-e^{2})\mu a}}}$
• énergie orbitale spécifique : ${\displaystyle \epsilon =-{\frac {\mu }{2a}}}$

avec :

• ${\displaystyle a\!\,}$ est la longueur du demi-grand axe
• ${\displaystyle \mu \!\,}$ est le paramètre gravitationnel standard (produit de la constante de gravitation G par la masse M du corps central).
• ${\displaystyle e\!\,}$ est l'excentricité orbitale définie par ${\displaystyle e={\frac {r_{\mathrm {ap} }-r_{\mathrm {per} }}{r_{\mathrm {ap} }+r_{\mathrm {per} }}}=1-{\frac {2}{{\frac {r_{\mathrm {ap} }}{r_{\mathrm {per} }}}+1}}}$

Attention : pour convertir la distance mesurée depuis les surfaces des objets en distance mesurée depuis les centres de gravité, il faut ajouter le rayon des objets en orbite ; et réciproquement.

La moyenne arithmétique des deux distances extrêmes est la longueur du demi-grand axe ${\displaystyle a\!\,}$ de l'ellipse orbitale. La moyenne géométrique de ces deux mêmes distances est la longueur du demi-petit axe ${\displaystyle b\!\,}$ de l'ellipse orbitale.

La moyenne géométrique des deux vitesses limites ${\displaystyle {\sqrt {-2\epsilon }}}$, est la vitesse correspondant à une énergie cinétique qui, à n'importe quelle position sur l'orbite, ajoutée à l'énergie cinétique courante, permettrait à l'objet en orbite de s'échapper de l'attraction. La racine carrée du produit des deux vitesses est donc la valeur locale de la vitesse de libération.