Backtesting
Le backtesting (France) ou test rétro-actif de validité (Canada) consiste à tester la pertinence d'une modélisation ou d'une stratégie en s'appuyant sur un large ensemble de données historiques réelles. Il peut être appliqué à tout ensemble de données, mais est le plus souvent utilisé dans les sciences sociales et les sciences naturelles qui produisent des données mesurables et nécessitent une approche statistique. En finance, il permet de vérifier la validité et la rentabilité d'une stratégie d'investissement[1]. Le plus souvent, la quantité de données nécessaires implique qu'elles soient centralisées dans une base de données, afin que le processus puisse être informatisé.
Backtesting en finance et en économie
Choix de stratégies d'investissement ou de spéculation sur les marchés financiers
Dans l'application de ces techniques aux marchés des capitaux, le backtesting est un type spécifique de tests historiques qui détermine la performance d'une stratégie financière, si elle avait été effectivement utilisée pendant des périodes passées et dans les mêmes conditions du marché. Le backtesting utilisant des données réelles est plus performant que des tests effectués sur des séries de données artificiellement simulées. Alors que le backtesting ne permet pas de prédire comment une stratégie fonctionnera dans les conditions futures, son principal avantage réside dans la compréhension de la vulnérabilité d'une stratégie grâce à son application à des conditions réelles effectivement rencontrées dans le passé. Cela permet au concepteur d'une stratégie d'«apprendre de ses erreurs», sans avoir à le faire avec de l'argent réel.
Un élément clé du backtesting qui le différencie des autres formes de tests historiques vient de ce qu'il calcule la performance si la stratégie avait réellement été appliquée dans le passé. Cela nécessite que le test reproduise les conditions du marché de l'époque en question afin d'obtenir un résultat précis. Des exemples de ces conditions de marché comprennent le suivi de cours, l'achat et la vente d'actions qui n'existent plus, ou l'utilisation d'indices de marché selon leur composition originelle, plutôt que leur composition actuelle. Historiquement, ces tests ont été utilisés par des institutions et des gestionnaires de fonds professionnels, en raison du coût d'acquisition de ces ensembles de données ou jeux de test. Toutefois, avec l'avènement des échanges boursiers sur internet, et la mise à disposition de bases de données plus accessibles, le backtesting est devenu une option pour les investisseurs ou spéculateurs occasionnels, et peut être ainsi inclus dans l'offre commerciale proposée par les courtiers en ligne.
Différents types de stratégies du marché des capitaux peuvent être back-testées, telles que les stratégies d'allocation d'actifs, les stratégies d'identification de signaux, des stratégies de négociation. D'autres types de stratégies se prêtent moins au backtesting, telles que les stratégies d'achats ou de ventes programmées pour de grandes quantités de titres au meilleur prix en répartissant les interventions sur une période de plusieurs heures, jours ou semaines. Cela vient du fait que vendre un même titre en grande quantité affecte son prix d'échange, et génère une décorrélation des conditions initiales en venant perturber la rétroactivité. Comme ces tests cherchent à évaluer l'exactitude de la corrélation et de la rétroactivité, le backtesting n'est pas approprié pour de telles stratégies.
Supervision bancaire
La supervision bâloise des risques bancaires s'appuie sur la détermination des montants de risque financier d'un ensemble de portefeuilles, la Value at Risk. Ces valeurs peuvent être déterminées à partir de modèles dynamiques paramétriques et semi-paramétriques [2],[3] ou à partir d'approches non paramétriques par simulations historiques ou encore par estimation kernel. Le comité de Bâle autorise les institutions financières à utiliser leur propres modèles – on parle alors de modèles internes – et ces derniers doivent être valides du point de vue des procédures de backtesting.
Le backtesting de la Value at Risk est fondé sur la notion d'exception ou encore de violation.[4],[5] Une exception se produit, si à une date donnée, la perte sur un portefeuille de titre est plus extrême que la Value at Risk. On parle d'exception car le risque se révèle plus grand que la mesure qui est supposée le couvrir. Parce que la Value at Risk n'est rien d'autre qu'un quantile sur la distribution des pertes du portefeuille, une façon typique de tester sa validité est de regarder si la proportion d'exception sur un échantillon est en adéquation avec le niveau de couverture des risques.
Pour une Value at Risk 1 jour à 99% backtesté 250 jours à la suite, le test est considéré vert (0-95%), orange (95-99.99%) ou rouge (99.99-100%) suivant la table suivante[6]:
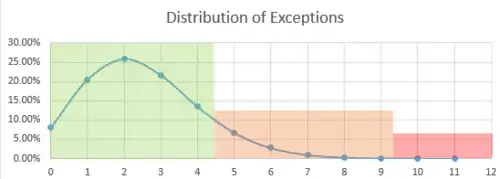
| Zone | Nombre d'exceptions | Probabilité | Cumul |
|---|---|---|---|
| Vert | 0 | 8.11% | 8.11% |
| 1 | 20.47% | 28.58% | |
| 2 | 25.74% | 54.32% | |
| 3 | 25.74% | 54.32% | |
| 4 | 13.41% | 89.22% | |
| Orange | 5 | 6.66% | 95.88% |
| 6 | 2.75% | 98.63% | |
| 7 | 0.97% | 99.60% | |
| 8 | 0.30% | 99.89% | |
| 9 | 0.08% | 99.97% | |
| Rouge | 10 | 0.02% | 99.99% |
| 11 | 0.00% | 100.00% | |
| ... | ... | ... |
Pour une Value at Risk 10 jours à 99% backtesté 250 jours à la suite, le test est considéré vert (0-95%), orange (95-99.99%) ou rouge (99.99-100%) suivant la table suivante:
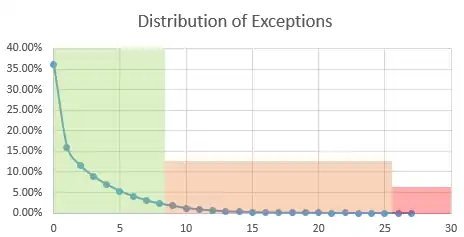
| Zone | Nombre d'exceptions | Probabilité | Cumul |
|---|---|---|---|
| Vert | 0 | 36.02% | 36.02% |
| 1 | 15.99% | 52.01% | |
| 2 | 11.58% | 63.59% | |
| 3 | 8.90% | 72.49% | |
| 4 | 6.96% | 79.44% | |
| 5 | 5.33% | 84.78% | |
| 6 | 4.07% | 88.85% | |
| 7 | 3.05% | 79.44% | |
| 8 | 2.28% | 94.17% | |
| Orange | 9 | 1.74% | 95.91% |
| ... | ... | ... | |
| 24 | 0.01% | 99.99% | |
| Rouge | 25 | 0.00% | 99.99% |
| ... | ... | ... |
Limites
Une des difficultés rencontrées dans le cadre des procédures standards de backtesting est le problème du risque d'estimation. Escanciano and Olmo ont souligné en 2010 que les tests de backtesting standards était susceptible d'être biaisés du fait de la non prise en compte du risque d'estimation des modèles utilisés pour estimer la Value at Risk. Ils proposent une correction de la statistique de test qui tient compte explicitement du risque d'estimation.
Backtesting et modélisation climatique
Le backtesting joue un rôle essentiel dans l'évaluation des modèles météorologiques et climatiques. Par exemple, pour composer une nouvelle théorie de la formation des cyclones, un modèle peut être back-testé avec les conditions réelles qui ont précédé et accompagné des ouragans. Si le modèle prévoit avec précision l'emplacement, la force, la trajectoire et la durée d'un événement passé, il gagne ainsi en crédibilité pour les prévisions futures. Dans le domaine de la modélisation du climat, le backtesting joue un rôle important en raison de l'ampleur et de la durée des événements climatiques. L'utilisation des données historiques pour valider de nouvelles théories permet d'évaluer leurs performances théoriques dans un délai raisonnable.
Maillage et effet papillon
Les difficultés pour valider un modèle réside dans la définition du maillage des données disponibles et testées, et dans la prise en compte de l'ensemble des paramètres variables discriminants. En raison de l'effet papillon, une très minime variation de données, d'une taille inférieure à celles des mailles des séries de données retenues, est susceptible de générer des divergences s'amplifiant avec le temps, de la même manière que le maillage du modèle lui-même[7].
Notes et références
- http://www.traderpack.fr/backtesting
- Robert F. Engle et Simone Manganelli, « CAViaR », Journal of Business & Economic Statistics, vol. 22, no 4, , p. 367–381 (ISSN 0735-0015, DOI 10.1198/073500104000000370, lire en ligne, consulté le )
- (en) Tim Bollerslev, « Generalized autoregressive conditional heteroskedasticity », Journal of Econometrics, vol. 31, no 3, , p. 307–327 (ISSN 0304-4076, DOI 10.1016/0304-4076(86)90063-1, lire en ligne, consulté le )
- (en) Paul H. Kupiec, « Techniques for Verifying the Accuracy of Risk Measurement Models », The Journal of Derivatives, vol. 3, no 2, , p. 73–84 (ISSN 1074-1240 et 2168-8524, DOI 10.3905/jod.1995.407942, lire en ligne, consulté le )
- Peter F. Christoffersen, « Evaluating Interval Forecasts », International Economic Review, vol. 39, no 4, , p. 841–862 (ISSN 0020-6598, DOI 10.2307/2527341, lire en ligne, consulté le )
- (en) Supervisory framework for the use of "backtesting" in conjunction with the internal models approach to market risk capital requirements, Basle Committee on Banking Supervision, (lire en ligne)
- Caractérisation de la variabilité interne des modèles régionaux de climat Philippe Lucas-Picher, Thèse de doctorat, Université du Québec à Montréal, août 2008
Articles connexes
- Portail des probabilités et de la statistique
- Portail de la finance