Value at risk
La VaR (de l'anglais value at risk, mot à mot : « valeur à risque », ou « valeur en jeu ») est une notion utilisée généralement pour mesurer le risque de marché d'un portefeuille d'instruments financiers. Elle correspond au montant de pertes qui ne devrait être dépassé qu'avec une probabilité donnée sur un horizon temporel donné.
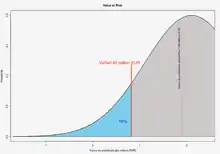
L'utilisation de la VaR n'est désormais plus limitée aux instruments financiers : on peut en faire un outil de gestion des risques dans tous les domaines (estimation du risque couru par une entreprise lié à la grippe A[réf. souhaitée], par exemple).
Pour calculer une VaR il est nécessaire de modéliser le portefeuille (et donc de faire des hypothèses). En particulier, cela suppose d'affecter une probabilité aux différentes évolutions possibles du portefeuille. La VaR est donc toujours conditionnelle à une modélisation d'un futur hypothétique qui possède nécessairement ses limites. Cette VaR peut être utilisée :
- Pour le calcul du capital économique ;
- Pour le suivi des risques de marché, à la fois en tant que reporting des risques et en tant qu'outil d'aide à la décision (pour allouer du capital à un "desk" par exemple) ;
- Pour le risque de crédit : voir Credit VaR
- Pour les exigences réglementaires (reporting réglementaire et exigences spécifiques).
Histoire
Cette notion est originaire du secteur de l'assurance. Elle a été importée à la fin des années 1980 sur les marchés financiers aux États-Unis par la banque Bankers Trust et popularisée par la banque JP Morgan en 1994 et son service (gratuit et public) Riskmetrics puis adoptée sous une forme embryonnaire par le Comité de Bâle (Bâle II) pour les banques et Solvabilité II pour les assurances.
Principales caractéristiques
La VaR d'un portefeuille dépend essentiellement de trois paramètres :
- la distribution des résultats des portefeuilles. Souvent cette distribution est supposée normale, mais beaucoup d'acteurs financiers utilisent des distributions historiques. La difficulté réside dans la taille de l'échantillon historique : s'il est trop petit, les probabilités de pertes élevées sont peu précises, et s'il est trop grand, la cohérence temporelle des résultats est perdue (on compare des résultats non comparables) ;
- le niveau de confiance choisi (95 ou 99 % en général). C'est la probabilité que les pertes éventuelles du portefeuille ou de l'actif ne dépassent pas la Value at Risk, par définition ;
- l'horizon temporel choisi. Ce paramètre est très important car plus l'horizon est long plus les pertes peuvent être importantes. Par exemple, pour une distribution normale des rendements, il faut multiplier la Value at Risk à un jour par pour avoir la Value at Risk sur jours.
D'une manière générale, la VaR donne une estimation des pertes qui ne devrait pas être dépassée sauf événement extrême sur un portefeuille pouvant être composé de différentes classes d'actifs.
Représentation formelle
La VaR est définie par rapport à un horizon de temps T et le seuil de confiance α (on parle par exemple de VaR 10 jours 95 %). La VaR T jours à une confiance α peut être définie (de manière équivalente) comme :
- La pire des pertes pouvant être constatée en T jours dans les α cas les plus favorables ;
- La moindre perte pouvant être constatée en T jours dans les 1-α ;
- Le montant au-delà duquel une perte survient en T jours avec une probabilité de 1-α ;
- La 100*αe (par exemple 95) perte des 100 pertes possibles les plus favorables ;
- La 100*(1-α)e (par exemple 5) perte des 100 pertes possibles les plus sévères ;
- Le αe quantile de la distribution des pertes possibles en T jours ;
- Le (1-α)e quantile de la distribution des gains possibles en T jours ;
Mathématiquement, la VaR est définie de manière implicite, à partir de la distribution du rendement de l'actif considéré sur la période considérée. Soit un nombre entre 0 et 1, et soit le rendement réalisé par l'actif. La est telle que: . La VaR ainsi définie est la perte qui a une probabilité d'être pire que le rendement du portefeuille ou de l'actif. Autrement dit c'est le quantile de la distribution des rendements du portefeuille ou de l'actif.
Limites et inconvénients de la VaR
Limite technique liée à la distribution de la perte qui n'est pas forcément normale, par exemple leptokurtique qui implique donc des évènements extrêmes plus fréquents que pour la loi normale. La VaR est aussi une fonction non convexe, ce qui fait que fusionner deux portefeuilles ne réduit pas forcément le risque. Ainsi elle ne constitue pas une mesure cohérente du risque. De plus, la VaR indique la perte potentielle maximale à un horizon de temps pour un niveau de confiance donné. Ainsi, la VaR ne donne aucune indication sur les valeurs prises une fois le seuil passé. En finance, on peut les étudier avec les Expected Shortfalls par exemple.
Backtesting
Le backtesting permet de valider la VaR en comparant les pertes prédites avec les pertes réalisées.
Le piller II des accords de Bâle II inclut une étape de backtesting.
Liens externes
- (fr) Article de vulgarisation
- (en) RiskGlossary.com
- Investopedia.com. (en) Première partie, Deuxième partie
Référence
Limites et inconvénients de la VaR.
- Ph. Jorion, "Value at Risk", Mc Graw Hill
- Portail de l’économie
- Portail de la finance