Tenseur des déformations

Le tenseur des déformations est un tenseur symétrique d'ordre 2 servant à décrire l'état de déformation local résultant de contraintes.

L'état de déformation d'un solide est décrit par un champ tensoriel, c'est-à-dire que le tenseur des déformations est défini en tout point du solide. On parle de ce fait de champ de déformation.

Dans le cadre de l'élasticité linéaire, le tenseur des déformations est relié au tenseur des contraintes par la loi de Hooke généralisée.

Définition de l'opérateur des déformations

Le tenseur des déformations vise à caractériser en un point la variation de longueur d'un segment à la suite de la transformation subie par le milieu. La déformation du milieu peut être décrite par la fonction (supposée suffisamment régulière) qui, à un point A du milieu, associe son transformé A' :

{\overrightarrow {OA'}}=\Phi (A,t)

Soit un segment AB qui se transforme en A' B'. Le tenseur des déformations permet de quantifier $\|{\overrightarrow {A'B'}}\|^{2}-\|{\overrightarrow {AB}}\|^{2}$ . On a en effet :

{\overrightarrow {OA'}}=\Phi (A,t)

On peut donc écrire :

{\overrightarrow {OB'}}={\overrightarrow {OA'}}+F\cdot {\overrightarrow {AB}}+o(\|{\overrightarrow {AB}}\|)

où

F={\rm {grad}}(\Phi )={\frac {\partial \Phi }{\partial A}}

est le gradient de la transformation $\Phi$ . D'où :

{\overrightarrow {A'B'}}=F\cdot {\overrightarrow {AB}}+o(\|{\overrightarrow {AB}}\|)

On obtient donc, au premier ordre :

\|{\overrightarrow {A'B'}}\|^{2}-\|{\overrightarrow {AB}}\|^{2}={\overrightarrow {AB}}^{T}\left(F^{T}\cdot F-{\rm {Id}}\right){\overrightarrow {AB}}

On pose :

E={\frac {1}{2}}\left(F^{T}\cdot F-{\rm {Id}}\right)

$E$ est l'opérateur des déformations de Green-Lagrange. Il s'agit d'un tenseur symétrique réel, donc diagonalisable dans une base orthonormée. Les directions propres sont appelées directions principales de déformation.

Si on introduit le vecteur déplacement

u(A,t)={\overrightarrow {AA'}}=\Phi (A,t)-{\overrightarrow {OA}}

on obtient :

F={\rm {Id}}+{\frac {\partial u}{\partial A}}

en notant ${\frac {\partial u}{\partial A}}$ la dérivée partielle de $u$ et donc :

E={\frac {1}{2}}\left({\frac {\partial u}{\partial A}}+{\frac {\partial u}{\partial A}}^{T}+{\frac {\partial u}{\partial A}}^{T}\cdot {\frac {\partial u}{\partial A}}\right)

Cas des petites déformations

Tenseur des déformations linéarisées

Si l'on fait l'hypothèse des petites déformations, on néglige les termes du second ordre et on obtient le tenseur des déformations linéarisé :

\varepsilon ={\frac {1}{2}}\left({\frac {\partial u}{\partial A}}+{\frac {\partial u}{\partial A}}^{T}\right)

Sous forme de composantes dans une base orthonormée :

\varepsilon _{ij}={1 \over 2}\left({\partial u_{i} \over \partial x_{j}}+{\partial u_{j} \over \partial x_{i}}\right)

Interprétation des termes diagonaux

Allongement du segment par déformation linéaire.

Les termes diagonaux $\varepsilon _{ii}$ sont les allongements relatifs dans la direction i (selon l'axe x_i). Prenons le cas d'un segment [AB], parallèle à l'axe x₁, et intéressons-nous à la partie de la déformation également parallèle à x₁, que nous noterons [A'B' ].

L'allongement relatif vaut (exprimée en distances algébriques) :

{\frac {{\overline {A'B'}}-{\overline {AB}}}{\overline {AB}}}

Sachant que

{\overline {AA'}}=u_{1}(A)

et

{\overline {BB'}}=u_{1}(B)

où $u_{1}$ est la composante de $u$ selon l'axe x₁, cet allongement vaut :

{\frac {{\overline {A'A}}+{\overline {AB}}+{\overline {BB'}}}{\overline {AB}}}-1={\frac {u_{1}(B)-u_{1}(A)+{\overline {AB}}}{\overline {AB}}}-1={\frac {u_{1}(B)-u_{1}(A)}{\overline {AB}}}

On reconnaît un taux d'accroissement de la fonction $u_{1}$ , et si l'on se place en petites déformations, on peut remplacer ce taux d'accroissement par la dérivée de $u_{1}$ , ce qui donne :

{\frac {{\overline {A'B'}}-{\overline {AB}}}{\overline {AB}}}\simeq {\frac {\partial u_{1}}{\partial x_{1}}}=\varepsilon _{11}

De manière plus générale :

\varepsilon _{ii}={\frac {\partial u_{i}}{\partial x_{i}}}={\frac {1}{2}}\left({\frac {\partial u_{i}}{\partial x_{i}}}+{\frac {\partial u_{i}}{\partial x_{i}}}\right)

Coefficients dus au cisaillement

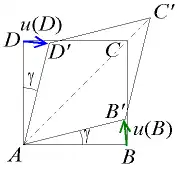
Effet de déplacement par le cisaillement.

Les autres termes $\varepsilon _{ij}$ (i ≠ j) sont les $\gamma$ , demi-variations de l'angle droit d'un petit volume de matière cubique avant déformation.

En effet, un carré ABCD, où [AB] est parallèle à x₁ et [AD] est parallèle à x₂, se transforme en un losange AB'C'D' , symétrique selon la première bissectrice du plan.

La tangente de l'angle $\gamma$ vaut :

\tan(\gamma )={\frac {\overline {BB'}}{\overline {AB}}}

.

Pour les petites déformations, on a

\tan(\gamma )\simeq \gamma

ainsi que

{\overline {BB'}}=u_{2}(B)\simeq u_{2}(A)+{\frac {\partial u_{2}}{\partial x_{1}}}\cdot {\overline {AB}}

avec u₂(A) = 0. Ainsi,

\gamma \simeq {\frac {\partial u_{2}}{\partial x_{1}}}

Si l'on considère maintenant le segment [AD] :

\gamma \simeq {\frac {\partial u_{1}}{\partial x_{2}}}

Une rotation n'étant pas une déformation, on peut supposer que les deux angles $\gamma$ sont égaux, quitte à faire pivoter le losange et ainsi

\gamma =\left({\frac {\partial u_{1}}{\partial x_{2}}}+{\frac {\partial u_{2}}{\partial x_{1}}}\right)=2\,\varepsilon _{12}

Note : dans l'article Déformation élastique, l'angle $\gamma$ défini vaut le double de l'angle défini ici.

Variation relative de volume

Variation de volume réelle (haut) et approchée (bas) : le dessin en vert montre le volume estimé et le dessin en orange le volume négligé

Considérons un prisme élémentaire engendré par trois vecteurs $(e_{10},e_{20},e_{30})$ . Sa transformée par $\Phi$ est le prisme engendré par $(e_{1},e_{2},e_{3})$ .

Soit V₀ celui du prisme initial et V le volume de la transformée.

On a, au premier ordre :

V=(e_{1}\wedge e_{2})\cdot e_{3}=(F(e_{10})\wedge F(e_{20}))\cdot F(e_{30})=\det(F)(e_{10}\wedge e_{20})\cdot e_{30}=\det(F)V_{0}

La variation relative de volume est ${\frac {V-V_{0}}{V_{0}}}={\frac {\Delta V}{V_{0}}}=\det(F)-1$

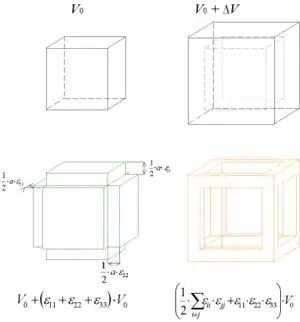
Dans le cas des petites déformations, $F={\rm {Id}}+{\frac {\partial u}{\partial A}}$ et det(F) - 1 est égal au premier ordre à la trace de ${\frac {\partial u}{\partial A}}$ , qui est égale à la trace du tenseur $\varepsilon$ : $\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}$

On peut retrouver ce résultat en se plaçant dans la base des directions principales de déformation. Considérons un cube d'arête a. Après déformation on a un quasi-parallélépipède de volume :

V=a\cdot (1+\varepsilon _{11})\times a\cdot (1+\varepsilon _{22})\times a\cdot (1+\varepsilon _{33})

alors que :

V_{0}=a^{3}

ce qui donne :

{\frac {\Delta V}{V_{0}}}={\frac {\left(1+\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}+\varepsilon _{11}\cdot \varepsilon _{22}+\varepsilon _{11}\cdot \varepsilon _{33}+\varepsilon _{22}\cdot \varepsilon _{33}+\varepsilon _{11}\cdot \varepsilon _{22}\cdot \varepsilon _{33}\right)\cdot a^{3}-a^{3}}{a^{3}}}

comme on est en très faible déformation,

1 >> ε_ii >> ε_ii·ε_jj >> ε₁₁·ε₂₂·ε₃₃

d'où le résultat.

On dit qu'il y a cisaillement pur lorsque la trace est nulle, autrement dit lorsqu'il n'y a pas de variation de volume.

Une déformation est dite incompressible si elle s'effectue sans variation de volume en tout point du corps. En particulier, les déformations plastiques s'effectuent sans variation de volume.

Déformations principales

Il existe une base orthonormée $({\vec {x}}_{\mathrm {I} },{\vec {x}}_{\mathrm {II} },{\vec {x}}_{\mathrm {III} })$ telle que le tenseur des contraintes est une matrice diagonale (voir Matrice symétrique > Décomposition spectrale) :

\mathrm {E} ={\begin{pmatrix}\varepsilon _{\mathrm {I} }&0&0\\0&\varepsilon _{\mathrm {II} }&0\\0&0&\varepsilon _{\mathrm {III} }\\\end{pmatrix}}

.

Les directions $({\vec {x}}_{\mathrm {I} },{\vec {x}}_{\mathrm {II} },{\vec {x}}_{\mathrm {III} })$ sont appelées directions principales, et les déformations ε_I, ε_II et ε_III sont les déformations principales.

Les déformations principales sont les valeurs propres du tenseur, et les directions propres, ses vecteurs propres. Les valeurs propres λ vérifient l'équation

\mathrm {det} (E-\lambda I)=0

où I est la matrice identité ; les déformations principales sont donc les solutions en λ de cette équation.

Rappelons que la trace est invariante par changement de base (voir Matrices semblables), donc

\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}=\varepsilon _{\mathrm {I} }+\varepsilon _{\mathrm {II} }+\varepsilon _{\mathrm {III} }

et ainsi en petites déformations, la variation relative de volume vaut

{\frac {\Delta \mathrm {V} }{\mathrm {V} _{0}}}=\varepsilon _{\mathrm {I} }+\varepsilon _{\mathrm {II} }+\varepsilon _{\mathrm {III} }

Contrairement aux contraintes principales, la notion de déformation principale est assez peu utilisée pour le calcul. Elle permet par contre d'exprimer de manière simple l'énergie élastique, et est utile pour dépouiller les résultats d'extensométrie. Par ailleurs, les directions principales sont les mêmes pour le tenseur des déformations et pour le tenseur des contraintes.

Invariants du tenseur des déformations

On définit trois invariants du tenseur, c'est-à-dire trois valeurs qui sont indépendantes de la base :

$I_{1}=\mathrm {Tr} (\mathrm {E} )=\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}=\sum _{i}\varepsilon _{ii}$

soit, avec la convention de sommation d'Einstein : $I_{1}=\varepsilon _{ii}$ ;

$I_{2}=\varepsilon _{11}\varepsilon _{22}+\varepsilon _{22}\varepsilon _{33}+\varepsilon _{33}\varepsilon _{11}-\varepsilon _{12}^{2}-\varepsilon _{23}^{2}-\varepsilon _{31}^{2}={\frac {1}{2}}\sum _{i}\sum _{j}(\varepsilon _{ii}\varepsilon _{jj}-\varepsilon _{ij}\varepsilon _{ij})$

ou encore $I_{2}={\frac {1}{2}}(\varepsilon _{ii}\varepsilon _{jj}-\varepsilon _{ij}\varepsilon _{ij})$ ;

$I_{3}=\mathrm {det} (\mathrm {E} )$

ou encore $I_{3}=e_{ijk}\varepsilon _{1i}\varepsilon _{2j}\varepsilon _{3k}$ où e_ijk est le symbole de Levi-Civita (ou symbole de Ricci). Avec les déformations principales, cela devient :

$I_{1}=\varepsilon _{I}+\varepsilon _{II}+\varepsilon _{III}$ ;
$I_{2}=\varepsilon _{I}\varepsilon _{II}+\varepsilon _{II}\varepsilon _{III}+\varepsilon _{III}\varepsilon _{I}$ ;
$I_{3}=\varepsilon _{I}\varepsilon _{II}\varepsilon _{III}$ .

Tenseur isotrope et déviateur

On peut exprimer le tenseur des déformations sous la forme d'un tenseur isotrope E' et d'un déviateur E'' :

\mathrm {E} =\mathrm {E} '+\mathrm {E} ''

avec le tenseur isotrope, également appelé partie sphérique

\mathrm {E} '={\frac {1}{3}}\mathrm {tr} (\mathrm {E} )\mathrm {I}

où I est la matrice unité, et le déviateur de déformation

\mathrm {E} ''=\mathrm {dev} (\mathrm {E} )=\mathrm {E} -\mathrm {E} '

.

On a, en utilisant la convention de sommation d'Einstein :

$\varepsilon '_{ij}={\frac {1}{3}}\left(\sum _{k}\varepsilon _{kk}\right)\delta _{ij}={\frac {1}{3}}\varepsilon _{kk}\delta _{ij}$ ;
$\varepsilon ''_{ij}=\varepsilon _{ij}-{\frac {1}{3}}\left(\sum _{k}\varepsilon _{kk}\right)\delta _{ij}=\varepsilon _{ij}-{\frac {1}{3}}\varepsilon _{kk}\delta _{ij}$ ;

où δ_ij est le symbole de Kronecker.

Cette décomposition simplifie l'expression des énergies de déformation élastique de changement de volume et de distorsion.

Voir aussi

Articles connexes

Tenseur des constantes élastiques (ou des rigidités)
Tenseur des souplesses

Liens externes

Émile Mathieu, Traité de physique mathématique (lire en ligne), « Déformations très petites d'un corps solide. » (sur Gallica)
tenseurs contrainte/déformation - loi de comportement élastique isotrope, orthotrope manuel de référence du logiciel de calcul de structure ICAB Force

Portail de la physique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.