Carré
En géométrie euclidienne, un carré est un quadrilatère convexe à quatre côtés de même longueur avec quatre angles droits. C’est donc un polygone régulier, qui est à la fois un losange, un rectangle, et par conséquent aussi un parallélogramme particulier.
Pour les articles homonymes, voir Carré (homonymie).
Pour l’article ayant un titre homophone, voir Kharé.
| Carré | |
| |
| Type | Polygone régulier |
|---|---|
| Symbole de Schläfli | {4} |
| Diagramme de Coxeter-Dynkin | |
| Groupe de symétrie | Groupe diédral D8 |
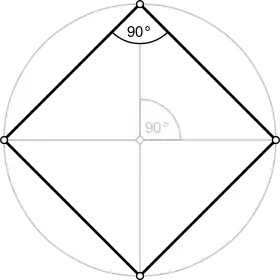
| Angle interne | 90° |
| Aire | a² |
| Périmètre | 4a |
| Propriétés | Constructible |
Dans le plan, un carré est invariant par quatre symétries axiales, par deux rotations d’angle droit et par une symétrie centrale par rapport à l’intersection de ses diagonales.
Les premières représentations du carré datent de la préhistoire. Le carré est, avec le cercle, l'une des figures géométriques remarquables les plus étudiées depuis l'Antiquité, le problème de la quadrature du cercle ayant tenu en haleine de nombreux mathématiciens pendant deux millénaires.
La figure du carré illustre l’opération du carré en algèbre, consistant à multiplier un élément par lui-même. En particulier, l’aire d’un carré est égale au carré de la longueur d’un côté.
Présentation
Composition

Un carré est une figure plane composée de quatre points appelés sommets et de quatre segments de même longueur, appelés côtés, reliant les sommets dans un ordre cyclique et formant successivement des angles droits orientés dans le même sens. Deux sommets reliés par un côté sont dits consécutifs, sinon ils sont opposés.
Les côtés constituent le bord d’une surface du plan appelée carré plein et qui est l’enveloppe convexe des sommets. Le carré plein privé de son bord est l’intérieur du carré.
Si les sommets du carrés sont nommés A, B, C et D dans cet ordre, le carré est noté et les caractéristiques ci-dessus s’écrivent et .
Les deux segments reliant les sommets opposés sont les diagonales du carré, qui sont perpendiculaires et de même longueur.
Les deux diagonales se croisent en leur milieu qui est appelé centre du carré. Ce point est à la fois l’isobarycentre des sommets et le centre de masse du carré plein.
Le centre du carré est aussi le centre d’un cercle circonscrit passant par les quatre sommets, de diamètre égal à la longueur des diagonales. Il est également le centre d’un cercle inscrit tangent aux quatre côtés en leur milieu respectif, et de diamètre égal au côté du carré.
Mesures
En notant c la longueur d’un côté, le périmètre du carré s’écrit et son aire vaut . Chaque diagonale a pour longueur , comme le montre l’application du théorème de Pythagore dans un triangle isocèle rectangle formé par une diagonale et deux côtés du carré. Ce rapport s’illustre aussi par le fait qu’un grand carré, admettant pour côté la diagonale du carré initial, se décompose en quatre triangles isocèles rectangles avec lesquels on peut reconstituer deux carrés de même taille que le carré initial.
Le carré est, parmi les quadrilatères de même périmètre, celui qui possède la plus grande surface. Cette figure est la réponse à la question d'isopérimétrie dans les quadrilatères.
Symétries
Les transformations isométriques laissant un carré globalement invariant sont :
- les symétries axiales par rapport à une diagonale ou une médiatrice d’un côté ;
- les rotations autour du centre du carré et dont l'angle est un multiple de l'angle droit, et en particulier la symétrie centrale par rapport au centre du carré.
En voici la liste, elles sont au nombre de huit et forment un groupe :
 id (identité : chaque point est conservé) |  r1 (rotation de 90° vers la droite) | 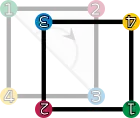 r2 (rotation de 180°) |  r3 (rotation de 270° vers la droite) |
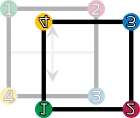 fv (retournement vertical) | 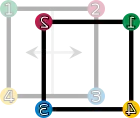 fh (retournement horizontal) | 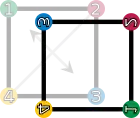 fd (retournement suivant la première diagonale) | 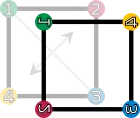 fc (retournement suivant la deuxième diagonale) |
| Les éléments du groupe de symétrie (D4). Les sommets sont colorés et numérotés uniquement pour visualiser les transformations. | |||
Le carré plein est alors engendré par un domaine fondamental triangulaire reliant le centre, le milieu d’un côté et une extrémité de ce côté. Le diagramme de Coxeter-Dynkin correspondant est constitué de deux points représentant les deux axes de symétrie bordant ce triangle (une diagonale et la médiatrice d’un côté), reliés par une arête marquée du chiffre 4 indiquant l’angle entre ces deux axes (45°, soit π/4 radians, un quart d’angle plat). Un cercle autour de l’un des points montre la présence d’un sommet sur l’un des axes (portant la diagonale).
Construction
Tous les carrés sont semblables. Cela signifie que, pour deux carrés donnés, il existe toujours un agrandissement (ou une réduction) permettant de transformer l'un en l'autre en conservant les angles géométriques et les proportions. Chaque carré est donc défini par sa position, son orientation et sa taille.
Un carré peut être défini par ses sommets, par son bord ou par son intérieur, mais aussi par l’une de ses diagonales, ou encore par la donnée de son centre et d’un sommet.
Étant donné un segment du plan, il existe deux carrés admettant ce segment pour côté, mais si le plan est muni d’une orientation préalable, le choix d’une orientation sur le segment (ou, ce qui revient au même, le choix d’un ordre sur ses extrémités) permet de définir sans ambiguïté l’un des deux carrés. Cette dernière méthode est par exemple utilisée dans le logiciel GeoGebra pour construire un carré comme polygone régulier à 4 sommets.
Construction au compas seul

On souhaite construire le carré de sommets ABCD connaissant seulement les points A et B. Posons R la distance entre A et B ; alors, on procède comme suit :
- on trace C1 le cercle de centre A et de rayon R (qui contient alors B)
⇒ on a un troisième point du carré sur ce cercle ; - on trace C2 le cercle de centre B et de rayon R (qui contient alors A)
⇒ le quatrième point du carré, C, se trouve sur ce cercle ; - Posons G un point d'intersection de C1 avec C2 ; on construit alors le point I, symétrique de B par rapport à A :
- on trace C3 centré en G et de rayon R ; ce cercle coupe C1 en B et en un autre point H,
- C4, de centre H et de rayon R, coupe C1 en G et en un nouveau point I ;
- posons S la distance entre G et I ; on construit alors C5 de centre I et de rayon S (il contient forcément G) ;
- C6 s'obtient en prenant pour centre B et pour rayon S (il contient forcément H) ; on note J le point d'intersection entre C6 et C5 qui est du même côté que G par rapport à la droite (AB) ;
- si T est la distance entre A et J, on construit C7 le cercle de centre A et de rayon T (il contient forcément J)
⇒ Le point C est obtenu par intersection entre C7 et C2 ; - on construit alors C8 de centre C et de rayon R
⇒ l'intersection de C8 et C1 est le point D.
Construction à la règle et au compas
Les animations suivantes montrent comment construire un carré à la règle et au compas.

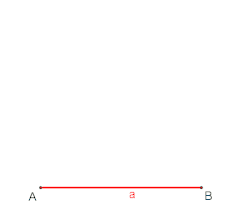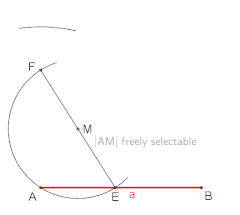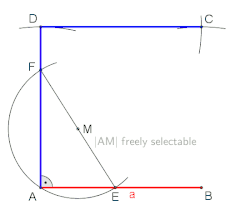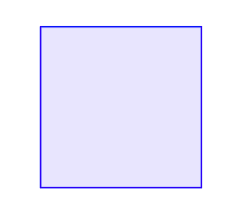 |
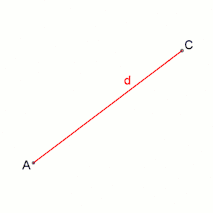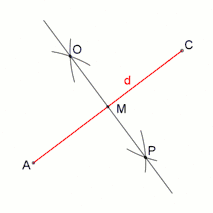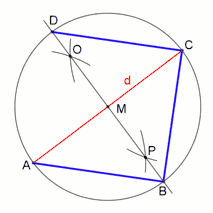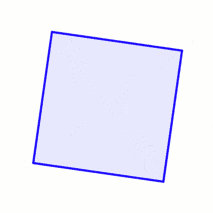 | |
Carré avec la longueur des côtés connue |
Carré avec la longueur des diagonales connue |
Problèmes associés
En dehors des problèmes de construction, la figure du carré est à l’origine de nombreux problèmes géométriques.
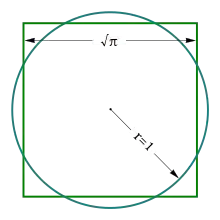 Quadrature du cercle
Quadrature du cercle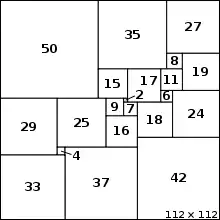 Quadrature parfaite du carré
Quadrature parfaite du carré Empilement de carrés dans un carré
Empilement de carrés dans un carré Carrés inscrits dans une courbe illustrant la conjecture de Toeplitz
Carrés inscrits dans une courbe illustrant la conjecture de Toeplitz
La quadrature du cercle est un problème de construction à la règle et au compas d’un carré ayant la même aire qu’un disque. Elle a été reconnue comme impossible du fait de la transcendance de π, démontrée par Ferdinand von Lindemann en 1882.
La quadrature du carré est la décomposition de la surface d’un carré plein de côté entier en un nombre fini de carrés pleins de côté entier, tous de taille différente. Plusieurs solutions ont été trouvées au cours du XXe siècle.
L’empilement de carrés dans un carré ou dans un cercle est la détermination de la taille maximale de n carrés superposables permettant une inclusion disjointe de leurs intérieurs dans un carré (ou un cercle) de taille donnée, en fonction du nombre n. Il n’y a pas de formule générale connue mais de nombreux empilements ont été proposés et l’optimalité de certains d’entre eux a été démontrée, pour de petites valeurs de n ou si ce nombre est déjà un carré parfait.
La conjecture de Toeplitz postule que toute courbe fermée simple contient quatre points distincts aux sommets d’un carré. Elle a été démontrée sous des hypothèses supplémentaires de régularité ou de symétrie sur la courbe, mais résiste dans un cadre général notamment sur certaines courbes fractales.
La subdivision d’un carré en carrés plus petits le long d’un quadrillage mène aussi à de nombreux problèmes exploités notamment comme jeux : le carré latin, le carré gréco-latin, le carré magique, le sudoku...
Histoire

Des poteries décorées de carrés sont attestées dès le VIe millénaire av. J.-C. en Mésopotamie[1].
Des tablettes démontrent la connaissance des symétries et rotations du carré vers le XVIIIe siècle av. J.-C.. La tablette BM 15285 contient une quarantaine de problèmes mathématiques concernant des aires de figures liées à des carrés[1].
L'Ancien Testament recommande de bâtir des villes de forme carrée, quelle que soit la forme de son enceinte[2].
Informatique
Unicode
Plusieurs caractères Unicode représentent des carrés. On peut synthétiquement les recenser dans le tableau suivant.
| Table des formes géométriques
(U+25A0 et suivants) |
Symboles divers et flèches
(U+2B00 et suivants) | |||
|---|---|---|---|---|
| Style | Grand | Moyen | Petit | Grand |
| carré noir plein | ■ (U+25A0) | ◼ (U+25FC) | ◾ (U+25FE) | ⬛ (U+2B1B) |
| carré blanc vide | □ (U+25A1) | ◻ (U+25FB) | ◽ (U+25FD) | ⬜ (U+2B1C) |
LaTeX
Dans le langage LaTeX, les extensions amsfonts et amssymb fournissent la commande \square pour mettre un carré en mode mathématique.
Notes et références
- (en) Eleanor Robson, Mathematics in Ancient Iraq: A Social History, Princeton University Press, , 442 p. (ISBN 9780691091822).
- Salomon Munk, Tanchum ben Joseph, Leopold Dukes et Isidore Cahen, La Bible : traduction nouvelle, .
Voir aussi
Articles connexes
Lien externe
Patrice Debart, « Le carré au collège », sur Descartes et les mathématiques
Bibliographie
Stella Baruk, « Carré » dans le Dictionnaire des mathématiques élémentaires, Éditions du Seuil, Paris 1995.
- Portail de la géométrie