Pesanteur

Pesanteur terrestre mesurée par le satellite GRACE de la NASA et de l'Agence aérospatiale allemande. Le graphique montre les écarts de la pesanteur réelle à la pesanteur normalisée associée à l'ellipsoïde homogène théorique modélisant la forme de la Terre. Les zones rouges sont celles où la pesanteur est plus élevée que la pesanteur théorique et les zones en bleu celles où elle est plus faible, l'amplitude totale de la variation (du bleu au rouge) étant de 1 mm/s².

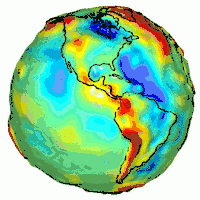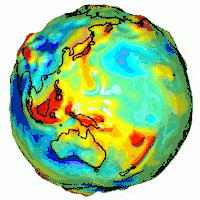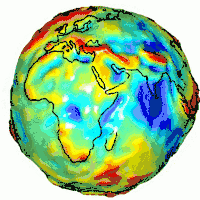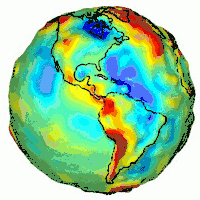
La Terre tournant sur elle-même et n'étant pas un astre sphérique et homogène, l'accélération de la pesanteur dépend du lieu et des facteurs suivants :

• la rotation terrestre : La rotation de la Terre sur elle-même entraîne une correction consistant à ajouter à l'accélération de la gravité une accélération d’entraînement axifuge, dirigée perpendiculairement à l'axe des pôles et de module : a = (2π/T)²d avec T = 86 164,1 s et d la distance en mètres entre l'objet et l'axe de rotation de la Terre. La correction, nulle aux pôles, atteint -0,3 % sur l'équateur ;
• la non-sphéricité de la Terre : À cause de l'aplatissement de la Terre, l'accélération de la gravité varie avec la latitude : elle est plus forte aux pôles qu'à l'équateur (0,2 % d'écart).
• l'altitude : Pour une variation de l'altitude h petite devant R, la variation relative de l'accélération de la gravité vaut -2h/R, soit −3,139 × 10⁻⁷ par mètre[alpha 4] à faible distance de la surface de la Terre ;
• les écarts de densité du sous-sol : ils entraînent des variations locales de la gravité que l'on néglige dans les formules générales devant la difficulté de les modéliser ;
• les forces de marée, notamment dues à la Lune et au Soleil. La correction correspondante varie au cours de la journée. Elle est de l'ordre de 2 × 10⁻⁷ à la latitude de 45° ;
• le mouvement du corps dans le repère terrestre : si un corps est en mouvement dans le repère terrestre, il subit une accélération complémentaire dite accélération de Coriolis, responsable notamment du mouvement de rotation des masses d'air (cyclones et anticyclones) et d'eau océanique (spirale d'Ekman). La composante verticale de cette accélération constitue la force d'Eötvös.

La formule suivante donne une valeur approchée de la valeur normale de l'accélération de la pesanteur en fonction de la latitude et pour une altitude faible devant le rayon terrestre (typiquement : quelques milliers de mètres)[6] :

${\displaystyle g=9{,}780\,327\times \left(1+5{,}302\,4\times 10^{-3}\times \sin ^{2}(\phi )-5{,}8\times 10^{-6}\times \sin ^{2}(2\times \phi )-3{,}086\times 10^{-7}\times h\right)}$

avec :

• g en m/s² ;
• h, altitude en m ;
• ϕ, latitude en radians dans le Système géodésique GRS 80 (1980)[7]^,[8].

La littérature sur ce point fait aussi mention de la formule suivante :

g = 9,7803267715 x (1 + 0,0052790414 sin2 ${\displaystyle \phi }$ + 0,0000232718 sin4 ${\displaystyle \phi }$ + 0,0000001262 sin6 ${\displaystyle \phi }$     + 0,0000000007 sin8 ${\displaystyle \phi }$)[4]

Pour les besoins pratiques, la Conférence générale des poids et mesures a défini en 1901[2]^,[3] une valeur normale de l'accélération de la pesanteur, à l'altitude 0, sur un ellipsoïde idéal approchant la surface terrestre, pour une latitude de 45°, égale à 9,806 65 m/s², soit 980,665 Gal (une unité dérivée de l'ancien système de mesure CGS, encore parfois usitée en gravimétrie, valant 1 cm/s²).

Dans le langage courant, on parle souvent de « g » comme unité de pesanteur égale à la valeur normale de la pesanteur terrestre soit 9,806 65 m/s². On lira par exemple que la pesanteur lunaire vaut 0,16 g, c'est-à-dire 0,16 fois la pesanteur normale terrestre, ou qu'un astronaute en centrifugeuse ou un pilote de chasse en virage subit une accélération de 6 g — six fois la pesanteur terrestre.

L'importance de la connaissance du champ de pesanteur de la Terre pour les géodésiens se conçoit aisément lorsqu'on sait que sa direction en chaque point, qui correspond à la verticale du lieu fournie par le fil à plomb, sert de référence lors de la mise en station de tout instrument de mesure géodésique. De manière plus détaillée, on comprend l'intérêt de la connaissance du champ de pesanteur pour les raisons suivantes :

• ses valeurs à la surface et à proximité de la Terre servent de référence à la plupart des quantités mesurées en géodésie. En fait, le champ de pesanteur doit être connu afin de réduire les observables géodésiques en systèmes définis géométriquement ;
• la distribution des valeurs de la pesanteur à la surface terrestre permet, en combinaison avec d'autres mesures géodésiques, de déterminer la forme de cette surface ;
• la non-sphéricité induit des perturbations des orbites des satellites, dont l'observation précise à quelques centimètres près par le système d'orbitographie DORIS fournit de précieuses indications sur les écarts à la forme sphérique ;
• la surface de référence la plus importante pour les mesures d'altitude — qu'on appelle le géoïde — est une surface de niveau du champ de pesanteur ;
• l'analyse du champ de pesanteur externe fournit des informations sur la structure et les propriétés de l'intérieur de la Terre. En rendant ces informations disponibles, la géodésie devient une science auxiliaire de la géophysique. C'est ce qui s'est passé de manière accélérée pendant les dernières décennies, avec l'avènement de la gravimétrie spatiale.

La gravimétrie est la mesure des variations et des irrégularités de la gravité terrestre ; toutefois, celle-ci n'est pas directement mesurable : il faut d'abord mesurer la pesanteur et affecter celle-ci des corrections nécessaires, tels les effets dus à la rotation de la Terre ou les effets dus aux marées – le déplacement des masses d'eau produit des variations périodiques de la pesanteur. Les mesures gravimétriques permettent de décrire l'inégale distribution des masses à l'intérieur de la Terre qui induit des irrégularités de la pesanteur selon le lieu.

En général, les variations relatives de g sont plus importantes pour le géodésien et le géophysicien que les valeurs absolues ; en effet, les mesures différentielles sont plus précises que les mesures absolues.

La variation maximale de g à la surface de la Terre atteint à peu près 5 gal (5 × 10⁻² m s⁻²), et est attribuable à la variation de g avec la latitude. Des variations à plus courtes longueurs d'onde, connues comme anomalies gravimétriques du géoïde, sont typiquement de quelques dixièmes à quelques dizaines de milligals (mgal). Dans certains phénomènes géodynamiques dont l'observation est devenue possible depuis peu de temps grâce aux progrès de l'instrumentation géodésique, on s'intéresse à des variations de g en fonction du temps dont l'amplitude atteint seulement quelques microgals (µgal). Des études théoriques (modes du noyau, variation séculaire de g) envisagent actuellement des variations de g se situant au niveau du nanogal (ngal).

En prospection gravimétrique et en génie civil, les anomalies significatives de g sont généralement comprises entre quelques microgals et quelques dixièmes de milligal. Pour fixer les idées, lorsqu'à la surface de la Terre on s'élève de trois mètres, la pesanteur varie d'environ 1 mgal.

Si l'objet n'est pas immobile par rapport à la Terre, l'accélération de Coriolis, proportionnelle à la vitesse de l'objet, s'ajoute à celle de la pesanteur. Elle est généralement trop faible pour avoir un effet notable, mais joue un rôle prépondérant dans les mouvements de l'air dans l'atmosphère, en particulier le vent.

Le savant italien Galilée (1564-1642) a été un des premiers à décrire et à quantifier approximativement la pesanteur terrestre. Par une expérience mythique réalisée du haut de la tour de Pise, il aurait constaté que des balles lourdes et de poids différents ont le même temps de chute, mais, quand il explique dans son Dialogue sur les deux grands systèmes du monde pourquoi il en est ainsi dans le vide, il justifie par des expériences de pensée : notamment en imaginant deux pierres de même poids et forme, chutant simultanément et reliées ou non par un lien, formant ainsi deux corps séparés de même poids ou bien un seul de poids double, mais ayant dans tous les cas la même vitesse de chute[9].

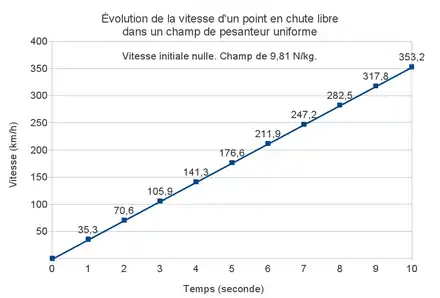
Vers 1604, Galilée utilise un constat : un objet en chute libre possède une vitesse initiale nulle, mais quand il arrive au sol, sa vitesse… n'est pas nulle. Donc la vitesse varie durant la chute. Galilée propose une loi simple : la vitesse varierait continûment à partir de 0, et proportionnellement au temps écoulé depuis le début de la chute. Ainsi : vitesse = constante × temps écoulé.

Il en conclut que, pendant une chute, la distance parcourue est proportionnelle au carré du temps écoulé. Plus précisément : distance = ½ constante × temps écoulé²  (avec la même constante que ci-dessus). Son idée est confirmée dans une expérience, avec du matériel construit de sa main : une gouttière inclinée le long de laquelle des clochettes sont disposées pour indiquer le passage de la bille.

Si un objet n'est pas pesé sous vide, son « poids » mesuré est égal au poids dû à sa masse diminué du poids du volume d'air déplacé (poussée d'Archimède). Sans cette correction, la mesure du poids d'un kilogramme de plume est inférieure à celle d'un kilogramme de plomb (du fait que le volume de ce kilogramme de plumes est plus important que le volume du même kilogramme de plomb et que la poussée d'Archimède est donc plus importante).

Le frottement de l'air provoque des forces aérodynamiques et en particulier de la traînée qui s'oppose au mouvement, ce qui fait qu'une petite boule tombe plus vite qu'une grosse de masse identique.

• (en) W.A. Heiskanen et H. Moritz, Physical Geodesy, W.H. Freeman and Company, 1967, San Francisco et Londres. ix + 364 pp, (ISBN 978-0716702337)
• (en) B. Hofmann-Wellenhorf et H. Moritz, Physical geodesy, Springer, 2005, (ISBN 978-3-211-33544-4)
• [Taillet, Villain et Febvre 2018] R. Taillet, L. Villain et P. Febvre, Dictionnaire de physique, Louvain-la-Neuve, De Boeck Sup., hors coll., janv. 2018, 4^e éd. (1^re éd. mai 2008), 1 vol., X-956, ill. et fig., 24 cm (ISBN 978-2-8073-0744-5, EAN 9782807307445, OCLC 1022951339, SUDOC 224228161, présentation en ligne, lire en ligne).

• Accélération normale de la pesanteur terrestre
• Astronautique
• Impesanteur
• Mécanique céleste
• Potentiel newtonien
• Propriétés du potentiel newtonien
• Gravité de surface

• Portail de la physique
• Portail de la géodésie et de la géophysique
• Portail de l’astronomie