Circuit équivalent de KLM

Le schéma présente trois ports : un port électrique, dont les deux terminaux correspondent aux deux électrodes placées sur les faces de la couche piézoélectrique, et deux ports mécaniques, qui, par le biais de l'analogie électro-mécanique, représentent la force et la vitesse sur chaque face.

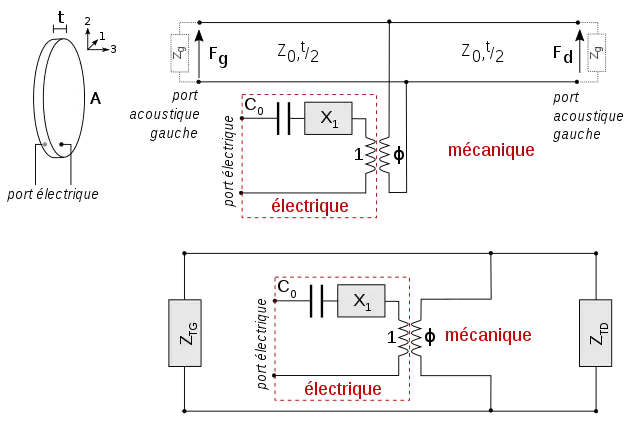
Les termes utilisés pour construire le schéma sont les suivants[4] :

• Géométrie :
  • ${\displaystyle A}$ la surface de la couche (en m²)
  • ${\displaystyle t}$ son épaisseur (m)
• Propriétés du matériau :
  • la rigidité du matériau dans l'axe 3 : ${\displaystyle C_{33}^{D}}$ (en N m⁻²) ;
  • la permittivité relative à déformation constante : ${\displaystyle \varepsilon _{33}^{S}}$ (adimensionnelle)
  • la constante piézoélectrique : ${\displaystyle h_{33}}$ (V/m).
  • la masse volumique : ${\displaystyle \rho }$ (kg m⁻³).
  • la célérité dans l'épaisseur : ${\displaystyle v^{D}={\sqrt {\frac {C_{33}^{D}}{\rho }}}}$
  • l'impédance mécanique : ${\displaystyle Z_{0}=A{\sqrt {C_{33}^{D}\rho }}}$
• l'impédance mécanique appliquée sur les deux faces : ${\displaystyle Z_{G}}$, ${\displaystyle Z_{D}}$ (gauche et droite)
• la fréquence angulaire ${\displaystyle \omega }$ (s⁻¹)
• le nombre d'onde ${\displaystyle \Gamma =\omega {\sqrt {\left({\frac {\rho }{c_{33}}}\right)}}}$
• Termes du schéma :
  • Capacité électrique statique : ${\displaystyle C_{0}={\frac {\varepsilon _{33}^{S}A}{t}}}$
  • coefficient de transformation ${\displaystyle \phi ={\frac {\omega Z_{0}}{2h_{33}}}csc\left({\frac {\Gamma t}{2}}\right)}$
  • Les impédances ramenées :
    • A gauche : ${\displaystyle Z_{TG}=\left({\frac {Z_{G}cos({\frac {\Gamma t}{2}})+iZ_{0}sin({\frac {\Gamma t}{2}})}{Z_{0}cos({\frac {\Gamma t}{2}})+iZ_{G}sin({\frac {\Gamma t}{2}})}}\right)}$
    • A droite : ${\displaystyle Z_{TD}=\left({\frac {Z_{D}cos({\frac {\Gamma t}{2}})+iZ_{0}sin({\frac {\Gamma t}{2}})}{Z_{0}cos({\frac {\Gamma t}{2}})+iZ_{D}sin({\frac {\Gamma t}{2}})}}\right)}$
  • Le terme de réactance ${\displaystyle X_{1}=i{\frac {h_{33}^{2}}{\omega ^{2}Z_{0}}}sin{(\Gamma t)}}$

Dans le cas où la couche piézoélectrique est « dans le vide », les deux ports mécaniques sont libres (pression nulle). On a donc ${\displaystyle Z_{G}=Z_{D}=0}$.

Il en ressort que ${\displaystyle Z_{TG}=Z_{TD}=Z_{0}tan\left({\frac {\Gamma t}{2}}\right)}$

L'impédance vue du port électrique vaut alors :

${\displaystyle Z_{free}={\frac {1}{iC_{0}\omega }}+X_{1}+{\frac {Z_{0}}{2\phi ^{2}}}tan\left({\frac {\Gamma t}{2}}\right)}$

Soit en remplaçant les termes par leur expression respective :

${\displaystyle Z_{free}={\frac {t}{i\varepsilon _{33}^{S}A\omega }}+i{\frac {h_{33}^{2}}{\omega ^{2}Z_{0}}}sin{(\Gamma t)}+{\frac {2h_{33}^{2}}{\omega ^{2}Z_{0}csc^{2}\left({\frac {\Gamma t}{2}}\right)}}tan\left({\frac {\Gamma t}{2}}\right)}$

On peut alors factoriser l'expression de la capacité et remplacer ${\displaystyle Z_{0}}$ par son expression :

${\displaystyle Z_{free}=\left({\frac {t}{i\omega A\varepsilon _{33}^{S}}}\right){\Biggl (}1+{\frac {A\varepsilon _{33}^{S}h_{33}^{2}}{\omega A{\sqrt {C_{33}^{D}\rho }}}}sin{(\Gamma t)}+{\frac {2i\varepsilon _{33}^{S}h_{33}^{2}}{\omega {\sqrt {C_{33}^{D}\rho }}}}{\frac {sin^{3}\left({\frac {\Gamma t}{2}}\right)}{cos\left({\frac {\Gamma t}{2}}\right)}}{\Biggr )}}$

On pose le coefficient de couplage électromécanique du mode épaisseur ${\displaystyle k_{t}}$, qu'il ne faut pas confondre avec le ${\displaystyle k_{33}}$ :

${\displaystyle k_{t}^{2}={\frac {\varepsilon _{33}^{S}h_{33}^{2}}{c_{33}^{S}}}}$

Par remplacement : ${\displaystyle Z_{free}=\left({\frac {t}{i\omega A\varepsilon _{33}^{S}}}\right){\Biggl (}1+k_{t}^{2}{\frac {\sqrt {C_{33}^{D}}}{\omega {\sqrt {\rho }}}}sin{(\Gamma t)}+k_{t}^{2}{\frac {2i{\sqrt {C_{33}^{D}}}}{\omega {\sqrt {\rho }}}}{\frac {sin^{3}\left({\frac {\Gamma t}{2}}\right)}{cos\left({\frac {\Gamma t}{2}}\right)}}{\Biggr )}}$

On identifie ${\displaystyle \Gamma }$ et on factorise ${\displaystyle k_{t}^{2}}$ :

Par remplacement : ${\displaystyle Z_{free}=\left({\frac {t}{i\omega A\varepsilon _{33}^{S}}}\right){\Biggl (}1+k_{t}^{2}{\Bigl (}{\frac {sin{(\Gamma )}}{\Gamma }}+{\frac {2i}{\Gamma }}{\frac {sin^{3}\left({\frac {\Gamma t}{2}}\right)}{cos\left({\frac {\Gamma t}{2}}\right)}}{\Bigr )}{\Biggr )}}$

D'où finalement :

${\displaystyle Z_{free}=\left({\frac {t}{i\omega A\varepsilon _{33}^{S}}}\right){\Biggl (}1-k_{t}^{2}{\frac {tan{\frac {\Gamma t}{2}}}{\frac {\Gamma t}{2}}}{\Biggr )}=\left({\frac {t}{i\omega A\varepsilon _{33}^{S}}}\right){\Biggl (}1-k_{t}^{2}{\frac {tan{\bigl (}{\frac {t\omega }{2}}{\sqrt {\frac {\rho }{C_{33}^{D}}}}{\bigr )}}{{\bigl (}{\frac {t\omega }{2}}{\sqrt {\frac {\rho }{C_{33}^{D}}}}{\bigr )}}}{\Biggr )}}$.

Cette expression, qui est la même qu'en utilisant le circuit équivalent de Mason est notamment utile pour déterminer les propriétés piézoélectriques du matériau par problème inverse, l'impédance électrique étant facile à mesurer expérimentalement[5].

La résonance se manifeste pour :

${\displaystyle {\frac {\Gamma t}{2}}={\frac {\pi }{2}}}$

${\displaystyle \omega _{\lambda /2}=\pi t{\sqrt {\frac {c_{33}}{\rho }}}}$

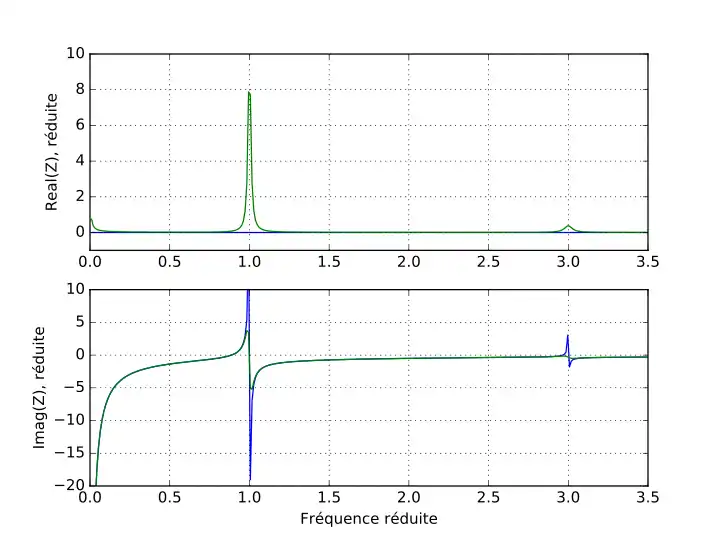
Dans l'expression ci-dessus, l'impédance est purement imaginaire (il n'y a donc aucune dissipation d'énergie) et diverge à la résonance. Cette situation n'est évidemment pas physique, et se résout en prenant en compte les pertes. Les pertes mécaniques se manifestent en ajoutant une petite partie imaginaire au ${\displaystyle c_{33}^{D}}$. De même, on ajoute une partie imaginaire au ${\displaystyle \varepsilon _{33}^{S}}$ pour représenter les pertes diélectriques, et au ${\displaystyle h_{33}}$ pour les pertes intrinsèques à l'effet piézoélectrique[6].

On représente ici l'impédance électrique réduite d'une plaque piézoélectrique libre, résonant dans son mode épaisseur, conformément à l'équation ci-dessus. En bleu, le modèle ne comprend pas de pertes, en vert, on a ajouté un taux de pertes de 1 %. La fréquence est réduite, c'est-à-dire que la fréquence correspondance à la résonance ${\displaystyle {\lambda /2}}$ est ramenée à 1. De même, la valeur de l'impédance est normalisée.

• Portail de la physique