Circuit RL
Un circuit RL est un circuit électrique contenant une résistance et une bobine ; il est utilisé dans diverses applications, comme filtre passe-bas ou passe-haut, ou dans les convertisseurs de courant continu. Contenant deux composants, il se décline en deux versions différant dans la disposition des composantes (série ou parallèle).
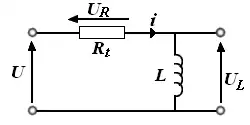
Circuit série
Le circuit en série est analysé avec la loi des mailles pour donner :
Régime transitoire
Dans le régime transitoire :
L'équation différentielle qui régit le circuit est alors la suivante :
Avec :
- U la tension aux bornes du montage, en V ;
- I l'intensité du courant électrique en A ;
- L l'inductance de la bobine en H ;
- Rt la résistance totale du circuit en Ω.
La solution générale, associée à la condition initiale Ibobine(t = 0) = 0, est :
Avec τ la constante de temps du circuit, en s.
C'est la constante de temps τ qui caractérise la « durée » du régime transitoire. Ainsi, le courant permanent est établi à 1 % près au bout d'une durée de .
Lorsque le courant devient permanent, l'équation se simplifie en U = RI car LdI/dt = 0.
Régime sinusoïdal permanent
Dans une analyse spectrale en régime sinusoïdal permanent, il faut considérer les impédances des composants en fonction de la pulsation :
où ω est la pulsation en rad.s-1, f est la fréquence en s-1 et j désigne l'unité imaginaire, telle que j2 = -1.
On pose Ue = U la tension entrant dans le quadripôle et Us la tension sortant du quadripôle. On a deux possibilités pour l'expression de Us :
On note HR(ω) et HL(ω) les fonctions de transfert de chaque cas respectif.
Analyse fréquentielle
La fonction de transfert peut s'écrire où G est le gain et φL, la phase.
Ainsi, avec :
Quand ω tend vers 0 :
Quand ω tend vers l'infini :
Ainsi, lorsque la sortie du filtre est prise sur la bobine le comportement est du type filtre passe-haut : les basses fréquences sont atténuées et les hautes fréquences passent.