Code identifiant d'un graphe
En mathématiques, et plus précisément en théorie des graphes, un code identifiant d’un graphe est un sous-ensemble de ses sommets tel que chaque sommet du graphe est identifié de façon unique par l’ensemble de ses voisins dans le code.
Historique
La théorie des graphes est un domaine combinant mathématiques discrètes et informatique. Son histoire remonte peut-être aux travaux d’Euler au XVIIIe siècle et trouve son origine dans l’étude de certains problèmes, tels que le célèbre problème des ponts de Königsberg qui consiste à déterminer s’il existe un parcours tel qu’il permettrait de faire le tour de la ville, et ce en partant d’un quartier au choix, en ne traversant qu’une seule et unique fois chaque pont de cette ville et de revenir au point de départ, ou encore celui du voyageur de commerce ainsi que le problème de coloriage de cartes (Théorème des quatre couleurs). La théorie des graphes s’est alors développée dans diverses disciplines telles que la chimie, la biologie, les sciences sociales. Depuis le début du XXe siècle, elle constitue une branche à part entière des mathématiques, grâce aux travaux de König, Menger, Cayley puis de Berge et d’Erdös.
De manière générale, un graphe permet de représenter la structure, les connexions d’un ensemble complexe en exprimant les relations entre ses éléments : réseaux de communication, réseaux routiers, interaction de diverses espèces animales, circuits électriques… etc. Les graphes constituent donc une méthode de pensée qui permet de modéliser une grande variété de problèmes en se ramenant à l’étude de sommets et d’arcs. Les derniers travaux en théorie des graphes sont souvent effectués par des informaticiens, du fait de l’importance qu’y revêt l’aspect algorithmique.
En 1998, M. Karpovsky, K. Charkrabary et Lev B. Levitin ont abordé le problème de couverture des sommets d’un graphe G de telle façon que l’on peut identifier d’une façon unique n’importe quel sommet de G. Ce fut là la première fois où la notion de codes identifiants a été utilisée.
Ces codes identifiants ont largement été étudiés depuis l’introduction du concept en 1998, où la théorie a été appliquée dans la modélisation du problème d’identification de processeurs défectueux dans les réseaux multiprocesseurs, et ultérieurement en 2003, par Ray et al. dans des réseaux de capteurs d’urgences.
Généralité sur les codes identifiants
Codes couvrants
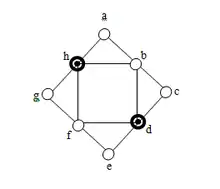
Soit un graphe non orienté et C un sous-ensemble de sommets du graphe G. Si C est tel que tout sommet v de V est voisin d’au moins un sommet de C, on dira alors que C est un code couvrant de G. Un code couvrant est aussi appelé dominant du graphe. Pour un sommet v de G, on définit le voisinage étendu de v comme l’ensemble :
Un sous-ensemble de sommets C est un code couvrant de G si et seulement si pour tout v ∈ V on a :
On dira qu’un sommet c ∈ C couvre le sommet v s’il appartient au voisinage étendu de v.
Codes séparateurs
Un sous-ensemble C’ de sommet du graphe G est un code séparateur de G si et seulement si :
ce qui est équivalent à dire :
Δ
Où Δ désigne la différence symétrique de deux ensembles: A Δ B = (A\ B) ∪ (B\ A) = (A∪ B) \ (A ∩ B)
On dira qu’un sommet c ∈ C sépare les sommets u et v s’il appartient à la différence symétrique de et .
Autrement dit, un code séparateur de G sépare toutes les paires de sommets distincts du graphe G.
La recherche d’un code séparateur d’un graphe G revient à résoudre un problème de couverture par tests dont l’instance est la matrice d’adjacence de G.
Définition d'un code identifiant
Un sous-semble C de sommets de G qui est à la fois un code couvrant et un code séparateur est appelé un code identifiant de G. Tous les sommets du graphe G sont donc couverts et séparés. On appelle pour chaque sommet v ensemble identifiant l’ensemble . On notera cet ensemble ou .
On a donc C qui est un code identifiant de G si et seulement si l’application :
est une injection dont l’image ne contient pas l’ensemble vide.
Le problème d’identification de processeurs défectueux
Comme nous l’avons mentionné plus haut, les codes identifiants ont été introduits pour modéliser un problème pratique d’identification de processeurs défectueux dans des réseaux multiprocesseurs.
On suppose que chaque processeur p d’un réseau soit capable d’exécuter une procédure test(p), qui s’applique à p ainsi qu’aux processeurs voisins de p. La procédure test(p) teste le bon fonctionnement de p ainsi que celui de ses voisins, et retourne une réponse de type binaire : 0 si une défaillance a été détectée sur p ou sur l’un de ses voisins, et 1 sinon. En supposant qu’à tout moment, au plus un processeur du réseau soit défectueux, le problème est de déterminer un sous ensemble de processeurs C tel que :
- Si au moins un des processeurs de C renvoie 0 après l’exécution de test, alors il y a un unique processeur défectueux dans le réseau, que nous sommes en mesure de localiser d’après les résultats des exécutions de test sur C
- Si tous les processeurs de C renvoient 1 après l’exécution de test, alors tous les processeurs du réseau sont en bon état de marche
Il est facile de voir qu’un sous-ensemble de processeurs C vérifie ces deux conditions si et seulement si l’ensemble de sommets correspondant C est un code identifiant du graphe associé au réseau.
Si aucun processeur du réseau n’est défectueux alors C est un code couvrant du graphe associé au réseau.
La première condition veut dire que C est un code séparateur du graphe. En effet, le sous-ensemble des processeurs de C voisin du processeur défectueux p : c’est l’ensemble identifiant de p.
Le problème de détection de feu
Le problème est de retrouver une pièce où un incendie s’est déclaré grâce aux réponses données par les détecteurs placés dans certaines pièces. Cela revient à chercher un sommet particulier, s’il existe, parmi tous les sommets d’un graphe G donné. On suppose que si un tel sommet existe il est unique. Savoir où placer les détecteurs revient à savoir quels sommets du graphe questionner. Pour cela nous allons choisir un ensemble C de sommets à « interroger », en posant la question suivante au sommet choisi : « existe-t-il un sommet en feu dans ton voisinage ? » :
- Si la réponse est 1 (oui), le sommet en feu peut être tout aussi bien lui que l’un de ses voisins.
- Si la réponse est 0 (non), on peut affirmer qu’il n’y a pas de sommet en feu dans l’ensemble C.
En supposant que C est un code identifiant, alors : après avoir interrogé tous les sommets du graphe, on puisse toujours affirmer : « il y a un sommet en feu et c’est celui-là » ou bien « il n’y a pas de sommet en feu dans ce graphe », et ce, quel que soit l’endroit où l’incendie peut se déclarer.
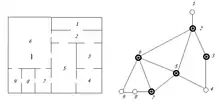
En prenant l’exemple de la figure, si on décide d’interroger un ensemble de sommet C (les sommets en noir) du graphe G et on aura les réponses suivantes :
| Sommet | Réponse |
|---|---|
| 2 | Oui |
| 3 | Non |
| 4 | Non |
| 5 | Non |
| 6 | Oui |
Ces réponses nous permettent d’affirmer qu’il y a au moins un sommet en feu, qui est voisin à la fois du sommet « 6 » et du sommet « 8 »; il y a donc seulement deux possibilités : l’un (ou plusieurs) des sommets « 1 » et « 2 » « 7 » « 8 » est en feu. Or les sommets « 2 » et « 7 » sont voisins du sommet « 5 » dont la réponse est non, ce qui exclut ces deux sommets, donc les sommets en feu sont les sommets « 1 » et « 8 ». Pour que l’ensemble C soit un code identifiant, il faut qu’il fonctionne pour retrouver n’importe quel sommet en feu.
Jeux et stratégies
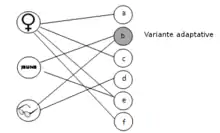
Le problème de recherche d’un sommet particulier (processeur défectueux ou pièce en feu) peut aussi s’appliquer sous une forme adaptative. Contrairement à la recherche d’un code identifiant où les sommets de l’ensemble sont interrogés un par un successivement, il s’agit ici d’adapter le code au fur et à mesure des réponses données. Dans ce cas, la recherche d’une solution optimale revient à minimiser le nombre d’interrogations. À l’image de nombreux jeux de devinettes populaires ou de jeux commerciaux comme le « Qui est-ce ? », expliqué dans ce qui suit :
- des personnes : a, b, c, d, e, f ;
- des caractéristiques : femme, jeune, lunettes ;
- les caractéristiques qui identifient le personnage mystère : il est jeune, mais ce n’est pas une femme.
Bibliographie
- Mark G Karpovsky, Krishnendu Chakrabarty et Lev B. Levitin, « On a new class of codes for identifying vertices in graphs », Information Theory, IEEE Transactions on, vol. 44, no 2, , p. 599-611 (lire en ligne)
- T. LEHOUILLIER, Codes identifiants dans les graphes, Travaux Études Recherches, Grenoble INP-ENSIMAG, 2009-2010.
- F. FOUCAUD, S. GRAVIER, R. NASERASI, A. PARREAU, P. VALICOV. Identifying codes in line graphs. LaBRI, Université de Bordeaux, CNRS. 2011. https://arxiv.org/abs/1107.0207
- F. FOUCAUD, R. NASERASR et A. PARREAU, Characterizing external digraphs for identifying codes and external cases of Bondy’s theorem on induced subsets. Graphs and Combinatorics manuscript. January 2012. http://www.lri.fr/~reza/pdfs/MaxIDCodeDigraph.pdf
- S. RAY, R. UNGRANGSI, F. De PELLEGRINI, A. TRACHTENBERG, et D. STAROBINSKY, Robust Location Detection in Emergency Sensor Networks, 2003. http://ipsit.bu.edu/documents/location_web.pdf http://ipsit.bu.edu/documents/jsac_web.pdf
- M. PASTORI. Les codes identifiants ou comment sauver le palais des flammes ? Découverte N°369. juillet-. p. 56-59
- Abdellah MALLEK, Codes identifiants dans les graphes : Théorie et applications, mémoire de Licence en Recherche Opérationnelle à l'Université des sciences et de la technologie Houari-Boumediene, proposé par M. Ahmed SEMRI, 2011-2012.
- Portail des mathématiques
- Portail de l'informatique théorique