Concept de solution
En théorie des jeux, on appelle concept de solution, ou type de solution, un ensemble de conditions que doivent vérifier les combinaisons (ou « profils ») de stratégies choisies par les joueurs pour qu'elles soient considérées comme des « solutions » du jeu. Ainsi le concept de solution « équilibre de Nash » impose pour condition que la stratégie de chaque joueur maximise son gain, les autres stratégies formant l'équilibre étant données. Un autre concept de solution est celui du « cœur » qui impose comme condition à une combinaison de stratégies d'être telle qu'il n'existe pas d'autre combinaison de stratégies dans laquelle certains joueurs pourraient augmenter leurs gains en quittant la coalition à laquelle ils appartiennent pour en former de nouvelles.
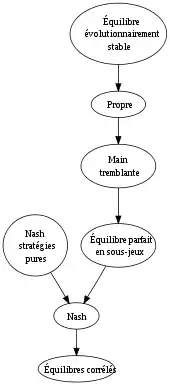
Si les conditions imposées par un concept de solution sont trop restrictives, alors le jeu risque de ne pas avoir de solution - selon ce concept de solution. Si elles sont plus lâches, il risque d'en avoir trop. Pour essayer de choisir entre des solutions multiples, les théoriciens des jeux proposent des « raffinements » du concept de solution - des conditions supplémentaires ; ce qui reporte le problème de la multiplicité des solutions sur celui des raffinements envisageables.
Rationalisabilité et dominance répétée
Dans ce concept de solution, on suppose que les joueurs sont rationnels et donc qu'ils éliminent les stratégies strictement dominées. Une stratégie strictement dominée est une stratégie telle qu'un joueur a toujours avantage à ne pas jouer, et donc qu'un joueur rationnel ne va jamais jouer (les stratégies strictement dominées sont également importantes dans la recherche du minimax par parcours d'arbre de jeu). Par exemple, dans le dilemme du prisonnier à une seule période tel qu'illustré ci-dessous, coopérer est strictement dominé par dévier pour les deux joueurs car chacun a avantage à jouer dévier quelle que soit la stratégie retenue par l'autre joueur.
| Prisonnier 1 Coopérer | Prisonnier 1 Dévier | |
|---|---|---|
| Prisonnier 2 Coopérer | ||
| Prisonnier 2 Dévier | -2, -2 |
Équilibre de Nash
Un équilibre de Nash est un profil de stratégie dans laquelle chaque stratégie est une meilleure réponse à l'ensemble des autres stratégies formant l'équilibre.
Induction à rebours
Il existe des jeux présentant plusieurs équilibres de Nash, dont certains sont peu réalistes, car reposant sur des stratégies qui ont rationnellement peu de chances d'être choisies. Dans le cas des jeux dynamiques, certains équilibres de Nash irréalistes peuvent être éliminés par induction à rebours, qui suppose que tous les coups futurs seront rationnels. Ce faisant, on élimine des menaces non crédibles car de telles menaces de jouer une stratégie dommageable à l'autre joueur en réponse à une stratégie donnée de sa part peuvent être non rationnelles à jouer une fois que l'autre joueur a quand même joué la stratégie en question.
Par exemple, considérons un jeu dynamique où les joueurs sont une entreprise établie dans un secteur d'activité et une entreprise pouvant entrer dans ce secteur. À l'état initial, l'entreprise établie jouit d'un monopole sur le secteur, et ne veut pas perdre de pouvoir de marché au profit de l'entrant. Si l'entrant potentiel choisit de ne pas entrer, le monopole maintient son profit élevé (profit de monopole M), et l'entrant ne perd ni ne gagne. Si l'entrant potentiel entre, le monopole peut soit engager une guerre des prix contre lui, ou s'accommoder de sa présence. On suppose qu'une guerre des prix peut conduire l'entrant à la faillite (en présence de coûts fixes F à l'entrée par exemple) et qu'elle réduit à zéro le profit du monopole. En revanche, si le monopole s'accommode de la présence de l'entrant, il peut ne perdre qu'une partie de son profit en partageant le marché dans le cadre d'un accord tacite (profits de duopole D et d).
| Guerre des Prix | S'accommoder | |
|---|---|---|
| Entrer | 0, -F | D, d |
| Ne pas entrer | M, 0 | M, 0 |
Si l'entrant potentiel entre effectivement, la meilleure réponse du monopole est donc de s'accommoder. Sachant cela, la meilleure réponse de l'entrant est d'entrer. Ainsi, le profil stratégique où l'entrant entre et le monopole s'accommode est un équilibre de Nash. Cependant, si le monopole choisit la guerre des prix, la meilleure réponse de l'entrant est de ne pas entrer. Si l'entrant n'entre pas, peu importe la stratégie prévue par le monopole. La guerre des prix constitue donc une meilleure réponse si l'entrant potentiel n'entre pas. Le profil où le monopole prépare la guerre des prix et où l'entrant potentiel n'entre pas est donc également un équilibre de Nash. Comme le jeu est dynamique, tout engagement du monopole à mener une guerre des prix en cas d'entrée n'est pas crédible, puisque si l'entrant potentiel entre quand même, le monopole aura avantage à s'accommoder plutôt que lutter. L'équilibre de Nash avec guerre des prix peut donc être éliminé par induction à rebours.
Équilibre de Nash parfait en sous-jeux
La perfection en sous-jeux constitue une généralisation de l'induction à rebours. L'induction à rebours suppose que tous les coups futurs seront rationnels. Dans un équilibre parfait en sous-jeux, les coups joués doivent constituer un équilibre de Nash dans chaque sous-jeu. L'induction à rebours ne peut être employée que dans le cas de jeux à nombre fini de coups et en information parfaite. Dans le cas de jeux infinis ou d'information imparfaite, la notion d'équilibre parfait en sous-jeux peut être employée. L'équilibre de Nash éliminé par induction à rebours dans la section précédente n'est pas non plus un équilibre en sous-jeux puisqu'il ne constitue pas un équilibre de Nash pour le sous-jeu correspondant au moment où l'entrant a décidé d'entrer.
Équilibre bayésien parfait
Article principal : Jeu bayésien
Parfois, la perfection en sous-jeux n'impose pas de restrictions suffisantes pour éliminer des stratégies déraisonnables. Par exemple, comme les sous-jeux ne peuvent discriminer à l'intérieur d'un même ensemble d'information, un jeu en information imparfaite peut avoir un seul sous-jeu, lui-même, et donc la perfection en sous-jeu ne peut éliminer aucun équilibre de Nash. Un équilibre bayésien parfait est une spécification des stratégies des joueurs et de leurs croyances à propos du nœud atteint dans un ensemble d'information donné. Une croyance au sujet d'un nœud est la probabilité qu'un joueur donné pense que ce jeu est ou sera partie du jeu (sur le chemin d'équilibre). En particulier, l'intuition de l'équilibre bayésien en sous-jeux est qu'il spécifie des stratégies rationnelles pour chaque joueur étant données les croyances de ce joueur ainsi que des croyances qui sont cohérentes avec les stratégies spécifiées.
Dans un jeu bayésien, une stratégie spécifie ce que joue un joueur dans chaque ensemble d'information contrôlé par ce joueur. La condition de cohérence entre les croyances et les stratégies est absente de la notion de perfection en sous-jeu. De ce fait, l'équilibre bayésien parfait constitue une condition de cohérence sur les croyances des joueurs. Tout comme dans un équilibre de Nash, aucune stratégie retenue dans un équilibre bayésien parfait ne peut être une stratégie strictement dominée, puisqu'en tout ensemble d'information, aucune stratégie retenue ne peut être strictement dominée en considérant le jeu commençant en cet ensemble d'information. Cela revient à dire que pour toute croyance que le joueur pourrait avoir en cet ensemble d'information, il n'existe pas de stratégie qui conduise à un paiement plus important pour ce joueur quelle que soit la stratégie de l'autre joueur. Contrairement à ce qui peut se passer dans les cas précédents, aucune stratégie d'équilibre ne peut être strictement dominée à partir d'un quelconque ensemble d'information, même si cette stratégie est hors du chemin d'équilibre. Ainsi, dans le cas d'un équilibre bayésien parfait, les joueurs ne peuvent menacer de jouer des stratégies strictement dominées à partir d'un quelconque ensemble d'information hors du chemin d'équilibre.
Le terme bayésien fait référence au fait que les joueurs mettent à jour leurs croyances en utilisant la formule de Bayes. Ils calculent les probabilités des différents coups à chaque étape étant donnés les coups qui ont déjà été joués.
Induction vers l'avant
Tout comme l'induction à rebours suppose que tous les coups futurs seront rationnels, l'induction vers l'avant suppose que les coups passés sont rationnels. Quand un joueur ne sait pas quel est le type de l'autre joueur (l'information est imparfaite et asymétrique), ce joueur peut concevoir une croyance sur le type de l'autre joueur en observant les actions passées de ce joueur. De ce fait, la croyance formée par ce joueur concernant la probabilité que l'autre joueur soit d'un type donné est fondée sur les coups passés de l'autre joueur en supposant que ce dernier est rationnel.
Références
- (en) Cho, I-K. & Kreps, D. M. (1987) Signaling games and stable equilibria. Quarterly Journal of Economics 52:179-221.
- (en) Harsanyi, J. (1973) Oddness of the number of equilibrium points: a new proof. International Journal of Game Theory 2:235-250.
- (en) Hines, W. G. S. (1987) Evolutionary stable strategies: a review of basic theory. Theoretical Population Biology 31:195-272.
- (en) Noldeke, G. & Samuelson, L. (1993) An evolutionary analysis of backward and forward induction. Games & Economic Behaviour 5:425-454.
- (en) Maynard Smith, J. (1982) Evolution and the Theory of Games. (ISBN 0521288843)
- (en) Selten, R. (1983) Evolutionary stability in extensive two-person games. Math. Soc. Sci. 5:269-363.
- (en) Selten, R. (1988) Evolutionary stability in extensive two-person games --- correction and further development. Math. Soc. Sci. 16:223-266
- (en) Thomas, B. (1985a) On evolutionary stable sets. J. Math. Biol. 22:105-115.
- (en) Thomas, B. (1985b) Evolutionary stable sets in mixed-strategist models. Theor. Pop. Biol. 28:332-341