Loi de la cryométrie

En chimie physique la loi de la cryométrie permet de quantifier l'abaissement de la température de fusion d'un solvant en fonction de la quantité de soluté ajouté.

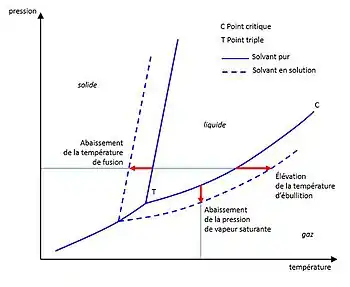
Diagramme de phases d'un solvant pur (courbes pleines) et du même solvant en présence d'un soluté (pointillés). Les propriétés colligatives se traduisent par un déplacement des courbes d'équilibre solide-liquide et gaz-liquide.

Elle est, avec la loi de la tonométrie et la loi de l'ébulliométrie, l'une des trois lois énoncées à partir de 1878 par François-Marie Raoult[1] concernant les propriétés colligatives d'une solution chimique liquide. Avec la loi de l'osmométrie, énoncée par Jacobus Henricus van 't Hoff en 1896 et concernant le phénomène de l'osmose, ces lois ont notamment permis d'établir des méthodes de détermination expérimentale de la masse molaire des espèces chimiques.

Remarques

Lorsque l'on parle des lois de Raoult[2] (au pluriel), on fait généralement allusion aux trois lois évoquées ci-dessus qu'il ne faut pas confondre avec la loi de Raoult (au singulier) concernant les équilibres liquide-vapeur idéaux.

Dans le monde anglo-saxon, cette loi est appelée loi de Blagden, du nom du chimiste Charles Blagden[3], assistant de Henry Cavendish, qui l'a mise en évidence expérimentalement dès 1788 sur des solutions aqueuses. Raoult généralisa cette loi, notamment en étudiant des solutions organiques[4].

Énoncé de la loi

Cas général

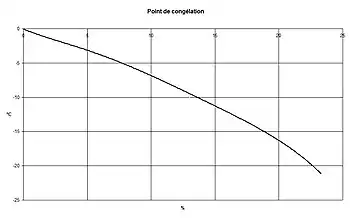
Température de fusion (congélation) d'une saumure de chlorure de sodium en fonction du pourcentage massique de sel dissout.
L'eau pure se solidifie à 0 °C, cette température décroît avec une augmentation de la concentration en sel. En raison de l'hypothèse de la solution idéale, la loi de la cryométrie n'est vraie qu'aux faibles concentrations, lorsque la courbe est approximativement linéaire. Aux fortes concentrations le mélange perd son comportement idéal et la loi ne s'applique plus sous cette forme.

Lorsque l'on considère un solvant $s$ contenant un soluté $\sigma$ , la température de solidification du solvant avec le soluté est plus basse que la température de solidification du solvant seul. La loi de la cryométrie s'énonce ainsi :

« L'abaissement de la température de solidification est proportionnel à la fraction molaire du soluté. »

Soit (en remarquant que pour un corps pur la température de solidification - ou température de congélation - est égale à la température de fusion) :

Loi de la cryométrie :

\Delta T_{\text{fus}}=K_{\text{cry}}\cdot x_{\sigma }

avec :

$\Delta T_{\text{fus}}$ l'abaissement de la température de fusion du solvant (en K) ;
$K_{\text{cry}}$ la constante cryoscopique du solvant (en K) ;
$x_{\sigma }$ la fraction molaire du soluté (en mol/mol).

La constante cryoscopique ne dépend que des propriétés du solvant :

Constante cryoscopique :

K_{\text{cry}}={R\,{T_{\text{fus}}}^{2} \over \Delta _{\text{fus}}H}

avec :

$R$ la constante universelle des gaz parfaits (en J/(K·mol)) ;
$T_{\text{fus}}$ la température de fusion du solvant pur (en K) ;
$\Delta _{\text{fus}}H$ l'enthalpie de fusion du solvant pur à $T_{\text{fus}}$ (en J/mol).

Sous cette forme, la constante cryoscopique a la dimension d'une température, elle s'exprime en kelvins (K).

Autrement dit, à pression constante, la température de fusion $T_{\text{fus}}$ du solvant pur passe à $T=T_{\text{fus}}-\Delta T_{\text{fus}}$ en présence d'un soluté. L'enthalpie de fusion étant une grandeur positive, la constante cryoscopique est positive. Ainsi l'ajout d'un soluté fait-il diminuer la température de fusion du solvant à pression constante ( $\Delta T_{\text{fus}}>0$ , soit $T<T_{\text{fus}}$ ).

La loi de la cryométrie a été établie expérimentalement, mais elle peut se démontrer théoriquement. Cette loi n'est valable que sous les hypothèses suivantes :

la quantité de soluté est négligeable devant celle du solvant dans la solution liquide ;
la solution liquide se comporte comme une solution idéale ;
la phase solide peut être considérée comme constituée de solvant pur, le soluté et le solvant n'étant pas miscibles en phase solide.

La loi de la cryométrie est une approximation aux faibles concentrations de l'équation de Schröder-van Laar qui peut être appliquée à des concentrations plus importantes.

En fonction de la molalité

La loi de la cryométrie est souvent exprimée en fonction de la molalité $b_{\sigma }$ du soluté, qui représente la quantité de soluté pour 1 kg de solvant (en mol/kg) :

Loi de la cryométrie :

T_{\text{fus}}-T=K_{\text{cry}}^{\prime }\cdot b_{\sigma }

La constante cryoscopique vaut alors :

Constante cryoscopique molale :

K_{\text{cry}}^{\prime }={R\,{T_{\text{fus}}}^{2} \over \Delta _{\text{fus}}H}{M_{s} \over 1000}

avec $M_{s}$ la masse molaire du solvant (en g/mol). Sous cette forme, la constante cryoscopique s'exprime en K·kg/mol, elle ne dépend toujours que des propriétés du solvant pur.

Démonstration

On note :

$M_{s}$ la masse molaire du solvant (en g/mol) ;
$m_{s}$ la masse de solvant (en g) ;
$n_{s}$ la quantité de solvant (en mol) ;
$n_{\sigma }$ la quantité de soluté (en mol).

On a, par définition de la fraction molaire, pour le soluté :

x_{\sigma }={n_{\sigma } \over n_{s}+n_{\sigma }}

Si la quantité de soluté est négligeable devant celle du solvant :

n_{\sigma }\ll n_{s}

x_{\sigma }\approx {n_{\sigma } \over n_{s}}

La masse de solvant est donnée par :

m_{s}=M_{s}\cdot n_{s}

La molalité du soluté est donnée par définition par :

b_{\sigma }={n_{\sigma } \over m_{s}}={n_{\sigma } \over M_{s}\cdot n_{s}}

On a par conséquent le rapport :

x_{\sigma }\approx M_{s}\cdot b_{\sigma }

La masse molaire étant exprimée le plus souvent en g/mol et la molalité en mol/kg, il est nécessaire d'introduire un facteur de conversion :

x_{\sigma }\approx {M_{s} \over 1000}b_{\sigma }

Pour un soluté dissociatif

Si le soluté se dissocie dans la solution liquide, comme un sel se dissociant en ions, l'expression de la loi est modifiée par le facteur de van 't Hoff $i$ :

Loi de la cryométrie :

T_{\text{fus}}-T=K_{\text{cry}}^{\prime }\cdot i\cdot b_{\sigma }

La constante $K_{\text{cry}}^{\prime }$ , elle, n'est pas modifiée.

Démonstration

Évolution du potentiel chimique du solvant en fonction de la température. La présence du soluté diminue le potentiel chimique du solvant liquide, ce qui augmente sa température d'ébullition et diminue sa température de fusion (congélation).

Pour un solvant pur au point de fusion, à sa température de fusion $T_{\text{fus}}$ , on a l'égalité des potentiels chimiques des deux phases solide et liquide :

(1)

\mu ^{\text{s,*}}\!\left(T_{\text{fus}}\right)=\mu ^{\text{l,*}}\!\left(T_{\text{fus}}\right)

avec :

$\mu ^{\text{s,*}}$ le potentiel chimique en phase solide pur ;
$\mu ^{\text{l,*}}$ le potentiel chimique en phase liquide pur.

On introduit, à pression constante, un soluté dans le solvant liquide. La température de fusion du solvant est modifiée et devient $T$ . Le potentiel chimique du solvant en phase liquide idéale $\mu ^{\text{l}}$ s'écrit, avec $x_{s}$ la fraction molaire du solvant dans cette phase :

\mu ^{\text{l}}\!\left(T\right)=\mu ^{\text{l,*}}\!\left(T\right)+RT\,\ln x_{s}

On considère qu'en phase solide le solvant est le seul constituant. Au nouvel équilibre de phase on a toujours l'égalité des potentiels chimiques :

\mu ^{\text{s,*}}\!\left(T\right)=\mu ^{\text{l}}\!\left(T\right)

on a donc :

(2)

\mu ^{\text{s,*}}\!\left(T\right)=\mu ^{\text{l,*}}\!\left(T\right)+RT\,\ln x_{s}

En soustrayant les termes de la relation (1) dans la relation (2) on a :

(3)

\mu ^{\text{s,*}}\!\left(T\right)-\mu ^{\text{s,*}}\!\left(T_{\text{fus}}\right)=\mu ^{\text{l,*}}\!\left(T\right)-\mu ^{\text{l,*}}\!\left(T_{\text{fus}}\right)+RT\,\ln x_{s}

La relation de Gibbs-Duhem donne la variation du potentiel chimique du solvant pur à pression constante :

\mathrm {d} \mu ^{*}=-{\bar {S}}^{*}\,\mathrm {d} T

avec ${\bar {S}}^{*}$ l'entropie molaire du solvant pur. On peut donc intégrer, en considérant une faible variation de température sur laquelle l'entropie molaire peut être considérée comme constante :

\int _{T_{\text{fus}}}^{T}\mathrm {d} \mu ^{*}=-{\bar {S}}^{*}\int _{T_{\text{fus}}}^{T}\mathrm {d} T

\mu ^{*}\!\left(T\right)-\mu ^{*}\!\left(T_{\text{fus}}\right)=-{\bar {S}}^{*}\cdot \left(T-T_{\text{fus}}\right)

On peut par conséquent réécrire la relation (3) :

-{\bar {S}}^{\text{s,*}}\cdot \left(T-T_{\text{fus}}\right)=-{\bar {S}}^{\text{l,*}}\cdot \left(T-T_{\text{fus}}\right)+RT\,\ln x_{s}

-\left({\bar {S}}^{\text{s,*}}-{\bar {S}}^{\text{l,*}}\right)\cdot \left(T-T_{\text{fus}}\right)=RT\,\ln x_{s}

avec ${\bar {S}}^{\text{s,*}}$ et ${\bar {S}}^{\text{l,*}}$ les entropies molaires respectives du solvant pur solide et liquide. En introduisant $\Delta _{\text{fus}}H=T_{\text{fus}}\cdot \left({\bar {S}}^{\text{l,*}}-{\bar {S}}^{\text{s,*}}\right)$ l'enthalpie de fusion du solvant :

\Delta _{\text{fus}}H\cdot \left(T-T_{\text{fus}}\right)=RT_{\text{fus}}T\,\ln x_{s}

Soit $x_{\sigma }=1-x_{s}$ la fraction molaire du soluté. Puisque $x_{\sigma }\approx 0$ , alors $\ln x_{s}=\ln \!\left(1-x_{\sigma }\right)\approx -x_{\sigma }$ par développement limité. Ainsi :

\Delta _{\text{fus}}H\cdot \left(T-T_{\text{fus}}\right)\approx -RT_{\text{fus}}T\,x_{\sigma }

T_{\text{fus}}-T={RT_{\text{fus}}T \over \Delta _{\text{fus}}H}x_{\sigma }

en considérant que $T\approx T_{\text{fus}}$ on a :

T_{\text{fus}}-T={R\,{T_{\text{fus}}}^{2} \over \Delta _{\text{fus}}H}x_{\sigma }

On obtient finalement la loi de la cryométrie :

Loi de la cryométrie :

T_{\text{fus}}-T=K_{\text{cry}}\cdot x_{\sigma }

Constante cryoscopique :

K_{\text{cry}}={R\,{T_{\text{fus}}}^{2} \over \Delta _{\text{fus}}H}

Applications

Cryométrie, détermination de la masse molaire du soluté

La cryométrie[5] est une technique permettant de déterminer la masse molaire d'un soluté.

On introduit une masse $m_{\sigma }$ de soluté dans une masse $m_{s}$ de solvant, on mesure la baisse $\Delta T_{\text{fus}}$ de la température de fusion du solvant.

Démonstration

On note :

$M_{\sigma }$ la masse molaire du soluté (en g/mol) ;
$m_{s}$ la masse de solvant (en g) ;
$m_{\sigma }$ la masse de soluté (en g) ;
$n_{\sigma }$ la quantité de soluté (en mol).

La masse de soluté vaut :

m_{\sigma }=M_{\sigma }\cdot n_{\sigma }

La molalité du soluté vaut :

b_{\sigma }={n_{\sigma } \over m_{s}}={1 \over M_{\sigma }}{m_{\sigma } \over m_{s}}

La température de fusion du solvant diminue de :

\Delta T_{\text{fus}}=K_{\text{cry}}^{\prime }\cdot b_{\sigma }

On peut en conséquence calculer la masse molaire du soluté selon :

M_{\sigma }={K_{\text{cry}}^{\prime } \over \Delta T_{\text{fus}}}{m_{\sigma } \over m_{s}}

La constante

K_{\text{cry}}^{\prime }

étant exprimée en K·kg/mol, on obtient ainsi une masse molaire en kg/mol, il est nécessaire d'introduire un facteur de conversion pour l'exprimer en g/mol.

La masse molaire $M_{\sigma }$ du soluté, en g/mol, est obtenue selon :

Masse molaire du soluté :

M_{\sigma }=1000{K_{\text{cry}}^{\prime } \over \Delta T_{\text{fus}}}{m_{\sigma } \over m_{s}}

Pour rappel, cette formule n'est valable que si la quantité de soluté est négligeable devant celle du solvant ( $m_{\sigma }\ll m_{s}$ ).

Exemple[6]

10,10 g de vanilline sont dissouts dans 500 g d'eau. La température de fusion de l'eau passe de 0 °C à −0,247 °C. La constante cryoscopique molale de l'eau est de 1,86 °C·kg/mol. L'abaissement de la température de fusion de l'eau vaut :

\Delta T_{\text{fus}}=0-\left(-0{,}247\right)=0{,}247\,{\mathsf {\text{°C}}}

La masse molaire de la vanilline est de :

M_{\text{vanilline}}=1000{1{,}86 \over 0{,}247}{10{,}10 \over 500}=152{,}11\,{\mathsf {\text{g/mol}}}

Constante cryoscopique

Le tableau suivant donne les constantes cryoscopiques de quelques solvants d'usage courant.

Note : un écart de température de 1 K étant égal à un écart de 1 °C, la constante cryoscopique peut indifféremment s'exprimer en K·kg/mol ou en °C·kg/mol.

Constante cryoscopique de quelques solvants[7]^,[8]
Solvant	Constante cryoscopique molale $K_{\text{cry}}^{\prime }$ (K·kg/mol)	Température de fusion $T_{\text{fus}}$ (°C)
Acide acétique	3,90[7] - 3,63[8]	16,64
Benzène	5,12[7] - 5,07[8]	5,5
Camphre	40[7] - 37,80[8]	180
Disulfure de carbone	3,8	-111
Tétrachlorure de carbone	30	-23
Naphtalène	6,94	80,2
Phénol	7,27[7] - 6,84[8]	43
Eau	1,86	0
Chloroforme	4,68	-64
Cyclohexane	20,80	6,47
Éthanol	1,99	-114
Nitrobenzène	6,87	6

Salage des routes, fluides frigoporteurs

Cette propriété colligative est utilisée par exemple en hiver lorsque les routes sont salées : l'épandage de sel fait fondre la neige en dessous de sa température de fusion normale. Les antigels sont des mélanges d'eau et de produits organiques (souvent des composés hydroxylés - alcool ou glycole), permettant également d'abaisser la température de fusion de l'eau.

Dans l'industrie, des saumures sont utilisées comme fluides frigoporteurs : des températures jusqu'à −55 °C peuvent être obtenues avec le chlorure de calcium CaCl₂, le chlorure de sodium NaCl ne permet pas de descendre en dessous de −21,2 °C. Des eaux carbonatées, glycolées ou ammoniaquées sont aussi employées[9]. Le tableau suivant donne la concentration en sel nécessaire pour obtenir une température de fusion d'une saumure de −40 °C.

Concentration en sel d'une saumure ayant une température de fusion de −40 °C[9]
Sel	Concentration massique (%)
Chlorure de calcium	25,7
Chlorure de magnésium	20
Carbonate de potassium	37
Acétate de potassium	39
Formate de potassium	41

Notes et références

Notes

Encyclopédie Universalis, « François Marie Raoult », sur Universalis.fr (consulté le 16 novembre 2020).
Académie nationale de Pharmacie, « Raoult (lois de) », sur dictionnaire.acadpharm.org (consulté le 16 novembre 2020).
Joseph William Mellor, Modern Inorganic Chemistry, New York, Longmans, Green, and Company, 1912 (lire en ligne), p. 161.
Y. Doucet, « L’évolution de la cryoscopie », J. Phys. Radium, vol. 3, n^o 10,‎ 1942, p. 177-188 (DOI 10.1051/jphysrad:01942003010017700, lire en ligne, consulté le 16 novembre 2020).
Dictionnaire Larousse, « Cryométrie », sur Larousse.fr (consulté le 16 novembre 2020).
Danielle Baeyens-Volant, Pascal Laurent et Nathalie Warzée, Chimie générale : chimie des solutions : Exercices et méthodes, Dunod, 2017 (ISBN 978-2-10-076593-5, lire en ligne), p. 64 et 72.
Atkins 1998, p. 137.
Claude Friedli, Chimie générale pour ingénieur, Lausanne/Paris, PPUR presses polytechniques, 2002, 747 p. (ISBN 2-88074-428-8, lire en ligne), p. 312.
Christophe Marvillet, Fluides frigoporteurs : Propriétés, vol. BE 9 752, Techniques de l'ingénieur, 2003, 13 p. (lire en ligne), p. 4.

Bibliographie

Détermination des poids moléculaires : mémoires de MM. Avogadro, Ampère, Raoult, van 't Hoff, D. Berthelot, Gauthier-Villars, 1938 (lire en ligne), sur Gallica.
Paul Arnaud, Françoise Rouquérol, Gilberte Chambaud, Roland Lissillour, Abdou Boucekkine, Renaud Bouchet, Florence Boulc'h et Virginie Hornebecq, Chimie générale : Cours avec 330 questions et exercices corrigés et 200 QCM, Dunod, coll. « Les cours de Paul Arnaud », 2016, 8^e éd., 672 p. (ISBN 978-2-10-074482-4, lire en ligne), p. 337-341.
Peter William Atkins, Loretta Jones et Leroy Laverman (trad. de l'anglais), Principes de chimie, Louvain-la-Neuve, De Boeck Superieur, 2017, 4^e éd., 1088 p. (ISBN 978-2-8073-0638-7, lire en ligne), p. 388-390.
Peter William Atkins et Julio De Paula, Chimie Physique, De Boeck Superieur, 2013, 4^e éd., 1024 p. (ISBN 9782804166519, lire en ligne), p. 172.
Peter William Atkins, Éléments de chimie physique, De Boeck Supérieur, 1998, 512 p. (ISBN 978-2-7445-0010-7, lire en ligne), p. 136-137.
Mohamed Ayadim et Jean-Louis Habib Jiwan, Chimie générale, Louvain, Presses universitaires de Louvain, coll. « Cours universitaires », 2013, 376 p. (ISBN 978-2-87558-214-0, lire en ligne), p. 260-261-262.
Danielle Baeyens-Volant, Pascal Laurent et Nathalie Warzée, Chimie des solutions : Exercices et méthodes, Dunod, coll. « Chimie générale », 2017, 320 p. (ISBN 978-2-10-076593-5, lire en ligne), p. 28-30.
John C. Kotz et Paul M. Treichel Jr (trad. de l'anglais), Chimie des solutions, Bruxelles/Issy-les-Moulineaux, De Boeck Supérieur, coll. « Chimie générale », 2006, 358 p. (ISBN 978-2-8041-5232-1, lire en ligne), p. 31-33.
Claude Strazielle, Caractérisation par la détermination des masses moléculaires, vol. PE 595, Éditions techniques de l'ingénieur, 1984 (lire en ligne), p. 3.

Voir aussi

Portail de la chimie
Portail de la physique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Encyclopédie Universalis, « François Marie Raoult », sur Universalis.fr (consulté le 16 novembre 2020).

[2] Académie nationale de Pharmacie, « Raoult (lois de) », sur dictionnaire.acadpharm.org (consulté le 16 novembre 2020).

[3] Joseph William Mellor, Modern Inorganic Chemistry, New York, Longmans, Green, and Company, 1912 (lire en ligne), p. 161.

[4] Y. Doucet, « L’évolution de la cryoscopie », J. Phys. Radium, vol. 3, n^o 10,‎ 1942, p. 177-188 (DOI 10.1051/jphysrad:01942003010017700, lire en ligne, consulté le 16 novembre 2020).

[5] Dictionnaire Larousse, « Cryométrie », sur Larousse.fr (consulté le 16 novembre 2020).

[6] Danielle Baeyens-Volant, Pascal Laurent et Nathalie Warzée, Chimie générale : chimie des solutions : Exercices et méthodes, Dunod, 2017 (ISBN 978-2-10-076593-5, lire en ligne), p. 64 et 72.

[Atkins-7] Atkins 1998, p. 137.

[Friedli-8] Claude Friedli, Chimie générale pour ingénieur, Lausanne/Paris, PPUR presses polytechniques, 2002, 747 p. (ISBN 2-88074-428-8, lire en ligne), p. 312.

[Marvillet-9] Christophe Marvillet, Fluides frigoporteurs : Propriétés, vol. BE 9 752, Techniques de l'ingénieur, 2003, 13 p. (lire en ligne), p. 4.