Flocon de Koch

Les 4 premières étapes de la construction.

Les 6 premières courbes successives en animation.

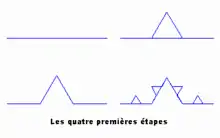
On peut la créer à partir d'un segment de droite, en modifiant récursivement chaque segment de droite de la façon suivante :

1. On divise le segment de droite en trois segments de longueurs égales.
2. On construit un triangle équilatéral ayant pour base le segment médian de la première étape.
3. On supprime le segment de droite qui était la base du triangle de la deuxième étape.

Au bout de ces trois étapes, l'objet résultant a une forme similaire à une section transversale d'un chapeau de sorcière.

La courbe de Koch est la limite des courbes obtenues, lorsqu'on répète indéfiniment les étapes mentionnées ci-avant.

Une extension de la notion de dimension permet d'attribuer à la courbe de Koch une dimension fractale (non entière) dont la valeur est[2]^,[3]^,[4]

${\displaystyle d={\frac {\ln 4}{\ln 3}}\approx 1{,}26}$

Intuitivement, on comprend que la courbe de Koch a une longueur infinie, parce qu'à chaque fois qu'on applique les modifications ci-avant sur chaque segment de droite, la longueur totale est multipliée par quatre tiers. Plus rigoureusement, on peut dire ceci: supposons que la courbe ait une longueur L. Alors chacune des quatre parties correspondant à la première division du segment initial a une longueur L/4; mais étant homothétiques de rapport 1/3 à la courbe totale, ces parties ont aussi une longueur L/3. Il s'ensuit que L/4 = L/3, et donc que L est soit nul - ce qui est impossible - soit infini.

La surface délimitée par la courbe est cependant finie, car contenue dans le demi-disque dont le diamètre est le segment initial. Si l'on a choisi l'unité d'aire de telle sorte que le triangle construit à la première itération soit d'aire 1, alors l'aire de chacun des quatre triangles construits lors de la seconde itération est 1/9 : on a donc augmenté l'aire totale de 4/9. Pour l'itération n, on ajoute ${\displaystyle 4^{n}\times \left({\frac {1}{9}}\right)^{n}}$. L'aire totale s'obtient finalement en sommant une série géométrique convergente :

${\displaystyle 1+\sum _{n=1}^{\infty }\left({\frac {4}{9}}\right)^{n}=1+{4/9 \over 1-4/9}=1+{\frac {4}{5}}={\frac {9}{5}}}$.

La courbe de Koch constitue un exemple de courbe continue mais non dérivable en chacun de ses points.

On peut considérer le flocon de Koch comme l'attracteur d'une famille de contractions, ce qui permet de prouver par exemple que c'est un compact de R²[5].

Création du flocon de Koch

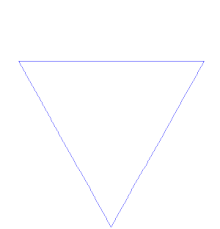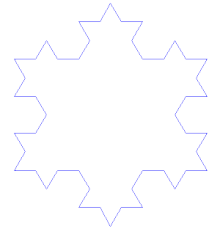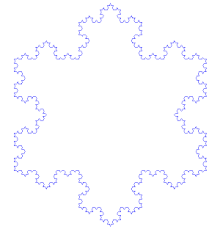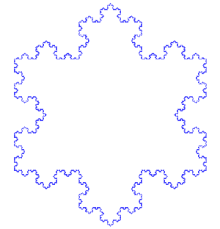
Le flocon de Koch s'obtient de la même façon que la fractale précédente, en partant d'un triangle équilatéral au lieu d'un segment de droite, et en effectuant les modifications en orientant les triangles vers l'extérieur. Pour un triangle initial (étape 0) de périmètre p, le périmètre du flocon à l'étape n est (4/3)ⁿp.

On peut aussi partir d'un hexagone, et opérer en orientant les triangles vers l'intérieur.

Dans les deux cas, après quelques itérations on obtient une forme évoquant un flocon de neige régulier.

Comme la courbe, le flocon de Koch est de longueur infinie et délimite une aire finie. Celle-ci est égale aux 8/5 de l'aire du triangle initial dû à la construction de seulement 3 triangles lors de la première étape.

Il est possible de paver le plan uniquement en utilisant des copies du flocon de Koch dans deux tailles différentes[6]^, [7].

Suivant le concept de von Koch, plusieurs variantes ont été conçues, en considérant des angles droits (Quadratique), d'autres angles (fractale de Cesàro) ou des extensions dans les dimensions supérieures (sphereflake, surface de Koch).

Variante	Illustration	Construction
1D & angle = 85°	Fractale Cesàro.	La fractale Cesàro est une généralisation de la courbe de Koch avec un angle compris entre 60° et 90° (ici 85°).
1D & 90°	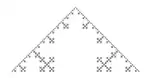Courbe quadratique de Koch (type 1)	Les 2 premières itérations.
1D & 90°	Courbe quadratique de Koch (type 2)	Les deux premières itérations. Sa dimension fractale égale 1,5, soit à mi-chemin entre la dimension 1 et la dimension 2. Cette propriété en fait une courbe très utilisée dans l'étude des propriétés physiques des objets fractals (cf. Sapoval).
2D & triangles	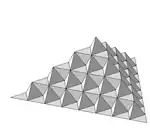Surface de von Koch	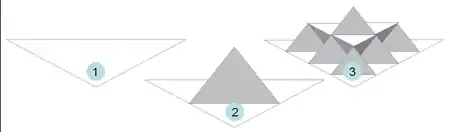Les 2 premières itérations. Extension naturelle à 2 dimensions de la courbe de von Koch.
2D & 90°	Surface quadratique de Koch (type 1)	Les trois premières étapes.
2D & 90°	Surface quadratique de Koch (type 2)	Les trois premières étapes.
2D & sphères	Sphereflake	Eric Haines a développé la fractale sphereflake (litt. flocon de sphère), extension du flocon de Koch, construite à base de sphères.