Dimension

Le terme dimension, du latin dimensio « action de mesurer »[1], désigne d’abord chacune des grandeurs d’un objet : longueur, largeur et profondeur, épaisseur ou hauteur, ou encore son diamètre si c'est une pièce de révolution.

L’acception a dérivé de deux façons différentes en physique et en mathématiques. En physique, la dimension qualifie une grandeur indépendamment de son unité de mesure, tandis qu’en mathématiques, la notion de dimension correspond au nombre de grandeurs nécessaires pour identifier un objet, avec des définitions spécifiques selon le type d’objet (algébrique, topologique ou combinatoire notamment).

Technique

Dans l'absolu, les dimensions d'une pièce peuvent être choisies de manière totalement arbitraire, l'important étant qu'elles soient compatibles avec l'utilisation finale de la pièce. Dans un but de normalisation, il est toutefois préférable d'utiliser comme dimensions linéaires nominales des valeurs de la « série de Renard ».

  • objet de 350 × 250 × 255 mm.
  • description : (L)ongueur × (l)argeur × (h)auteur.
  • forme : D = (L × l × h)
  • L’impression 4D opère sur des matériaux à mémoire de forme, déformables sous l’influence de la température ou de la lumière.
  • Le Standard Dimension Ratio est le rapport entre le diamètre extérieur d’un tube et l’épaisseur de sa paroi.

Physique

En physique, le terme « dimension » renvoie à deux notions complètement différentes.

Dimension d'un espace

La physique utilise beaucoup la notion mathématique d'espace vectoriel. On peut simplifier sa définition en disant que la dimension d'un espace est le nombre de variables qui servent à définir un état, un évènement. Ainsi, on dit classiquement que notre univers est à quatre dimensions, puisqu'un évènement se définit par la position dans l'espace (x, y, z) et l'instant t auquel cet évènement survient (il faut cependant préciser que, tant qu'aucune théorie physique ne relie le temps à l'espace, on pourrait tout aussi bien considérer la température comme une cinquième dimension ; l'article espace-temps explique comment la théorie de la relativité donne un sens non arbitraire à cette construction).

  • Un objet volumique constant (c'est-à-dire dont les propriétés sont indépendantes du temps, du moins durant l'étude) est dit à trois dimensions, car il faut trois nombres (x, y, z) pour désigner un de ses points ;
  • un objet plan (comme une feuille de papier) dont on néglige l'épaisseur est dit à deux dimensions, car il faut deux nombres (x, y) pour désigner un de ses points ;
  • un objet linéaire (comme un fil) dont on néglige l'épaisseur est dit à une dimension, car il suffit d'un seul nombre x pour désigner un de ses points (abscisse curviligne) ;
  • un objet ponctuel (comme un point) dont on néglige la taille est dit de dimension zéro, car une fois que l'on a désigné le point, on n'a besoin d'aucun paramètre supplémentaire pour le trouver.

Ces concepts sont repris en modélisation informatique (objet 2D, 3D).

Plus généralement, si un système physique peut être dans un ensemble d'états caractérisés par des mesures, le nombre de dimensions de cet ensemble d'états (appelé parfois espace des phases) est le nombre de variables indépendantes nécessaire pour caractériser un de ces états ; cela correspond mathématiquement à la notion de dimension d'une variété.

Dimensions supplémentaires

Il semble évident que l'espace physique n'a que trois dimensions, et on a longtemps considéré qu'une quatrième dimension spatiale était inimaginable, et en tout cas sans aucun sens physique concevable (voir l'article Espace à quatre dimensions pour plus de détails). Cependant, plusieurs modèles physiques contemporains, tentant en particulier de réconcilier relativité générale et physique quantique, supposent l'existence de dimensions spatiales supplémentaires, dites « enroulées », c'est-à-dire qu'un déplacement dans une de ces directions ramène au point de départ ; dans certains modèles de la théorie des cordes, il existerait ainsi 6 dimensions supplémentaires, totalement inaccessibles à notre échelle, car enroulées sur des longueurs comparables à la longueur de Planck.

Dimension d'une grandeur

La dimension est aussi une qualité commune à toutes les grandeurs qui peuvent s’exprimer avec les mêmes unités. Ainsi, la longueur, la hauteur, la distance, le diamètre ou la circonférence relèvent toutes de la même dimension, tandis qu’une autre rassemble l’énergie, la chaleur ou le travail.

Une grandeur sans dimension ou adimensionnée est un rapport de grandeurs de même dimension, comme un angle, définis sur un cercle comme le rapport de la longueur d'un arc de cercle donné sur le rayon de ce cercle.

L’analyse dimensionnelle est l’étude des différentes dimensions physiques et de leurs relations.

Autres acceptions
  • La dimension de Kolmogorov est l’échelle spatiale à partir de laquelle la viscosité permet de dissiper l’énerge cinétique d’un écoulement.
  • La dimension critique est une contrainte sur la dimensionnalité de l’espace-cible en théorie des cordes.
  • La réduction dimensionnelle est une procédure qui s’applique à une théorie formulée sur un modèle d’espace-temps pour obtenir une théorie formulée sur un sous-espace de dimension inférieure.

Mathématiques

Algèbre
  • La dimension d'un espace vectoriel est le cardinal commun à toutes les bases de cet espace, qu’il soit fini ou infini. Le cas de la dimension finie est l’objet du théorème de la dimension.
  • La dimension d'un espace affine est la dimension de l’espace vectoriel des translations associé.
  • La dimension de Krull d’une variété algébrique est le supremum des chaines d’inclusion de sous-variétés irréductibles.
  • La dimension projective (resp. injective, plate) d'un module est la borne inférieure des longueurs de ses résolutions projectives (resp. injectives, plates).
  • La dimension homologique (globale, à droite ou à gauche) d’un anneau est la borne supérieure des dimensions projectives ou injectives de ses modules (à droite ou à gauche).
  • La dimension globale faible d’un anneau est la borne supérieure des dimensions plates de ses modules (à droite ou à gauche).

Géométrie
  • L’espace à quatre dimensions est une extension des trois dimensions de la géométrie dans l’espace.
  • La dimension d'un convexe est la dimension de l’espace affine engendré.
  • La dimension de Hausdorff est un exposant critique associé au nombre de boules nécessaires pour recouvrir un fermé dans un espace géométrique.
  • La dimension de Minkowski-Bouligand (box-counting) a une définition semblable à celle de Hausdorff mais avec des boules (ou des pavés) de même taille.
  • La dimension de packing est duale de la dimension de Hausdorff en considérant le maximum de boules disjointes centrées sur la figure considérée.
  • La dimension fractale peut correspondre à plusieurs notions :
    • la dimension d’homothétie pour une figure présentant une autosimilarité ;
    • la dimension de corrélation et la dimension d'information parmi d’autres dimensions de Renyi, adaptées à l’étude d’attracteurs notamment ;
    • la dimension divider qui s’applique aux courbes sans auto-intersection ;
    • la dimension d'Assouad est la borne supérieure des dimensions de Hausdorff au voisinage de chaque point.

Topologie
  • La dimension d'une variété topologique est la dimension de l’espace image des cartes locales qui constituent son atlas.
  • Topologie en basses dimensions
  • Topologie d'un espace vectoriel de dimension finie
  • La dimension topologique d’un espace topologique peut être définie par :
    • la petite dimension inductive ou dimension de Urysohn-Menger et la grande dimension inductive ou dimension de Čech, toutes deux définies de façon récursive à partir de fermés séparants,
    • la dimension de recouvrement de Lebesgue, obtenue à partir du nombre d’ouverts d’intersection non vide d’un recouvrement de l’espace considéré.
  • La dimension combinatoire est la longueur maximale d’une chaine d’inclusions strictes de fermés irréductibles non vides, essentiellement utilisée en géométrie algébrique pour la topologie de Zariski.

Combinatoire
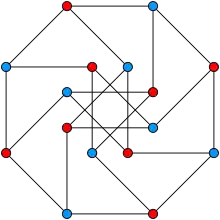
Le graphe de Möbius-Kantor dessiné dans un plan (dimension 2) avec des arêtes de longueur 1.
  • La dimension d'un graphe est celle du plus petit espace affine euclidien dans lequel le graphe peut être plongé avec des segments de longueur 1 comme arêtes.
  • La dimension bipartie d’un graphe est le nombre minimum de sous-graphes bipartis complets nécessaires pour couvrir toutes les arêtes.
  • L’appariement à 3 dimensions est une généralisation du couplage à une situation ternaire.

Algorithmique

Informatique

Art et culture

La quatrième dimension est un thème d’inspiration. Dans le domaine de la science-fiction, la quatrième dimension désigne, soit une quatrième dimension spatiale (en ajout avec la longueur, la largeur et la hauteur) qui serait responsable de faits insolites (cf : Théorie d'Everett) ; soit une autre dimension, celle-ci, temporelle et non spatiale : c'est-à-dire l'espace-temps à travers lequel les protagonistes pourraient voyager (cf : vitesse supraluminique).

Par extension, le terme « dimension » a finalement été utilisé pour caractériser les mondes dits « parallèles », c'est-à-dire par lesquels on ne peut pas accéder en voyageant dans l'espace ; on ne peut y accéder qu'en utilisant un appareil ouvrant une « faille » entre les « dimensions », ou bien à l'occasion d'un évènement accidentel. On dit que le monde parallèle est situé dans une « autre dimension ».

Littérature

Musique

Cinéma

Le cinéma 4D intègre à la projection des effets spéciaux supplémentaires tels que des mouvements des sièges.

Radio et télévision

Jeux vidéo

Sociétés
  • La Dimension septentrionale est un programme de l’Union européenne de coopération transfrontalière.
  • Dimension Data est une société sud-africaine de services en ingénierie informatique ayant aussi sponsorisé une équipe cycliste.

Notes et références
  1. « Dimension », dans Dictionnaire historique de la langue française, Paris, Dictionnaires Le Robert-Sejer,

Autres projets
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.