Dimension (théorie des graphes)
En mathématiques, et plus particulièrement dans la théorie des graphes, la dimension d'un graphe est le plus petit nombre entier tel qu'une représentation classique du graphe[1] dans l'espace affine euclidien de dimension ne comporte que des segments de longueur 1.
Cet article concerne la dimension d'un graphe. Pour sa dimension métrique ou sa dimension bipartie, voir Vocabulaire de la théorie des graphes. Pour la notion générale de dimension, voir Dimension.
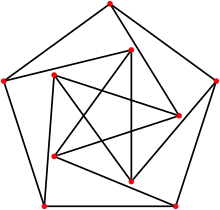
Dans cette définition, les sommets doivent être distincts, mais il n'y a pas de contraintes sur le croisement des arêtes. On note la dimension d'un graphe ainsi : .
Par exemple, le graphe de Petersen peut être tracé avec des segments de longueur 1 sur le plan euclidien , mais pas sur la droite : sa dimension est 2 (figure).
Cette notion a été introduite en 1965 par Paul Erdős, Frank Harary et William Tutte[2]. Elle généralise à une dimension quelconque la notion de graphe distance-unité du plan .
Exemples

Graphe complet
Dans le pire des cas pour un graphe, tous les sommets sont reliés, c'est le graphe complet.
Il faut un espace euclidien de dimension pour y plonger le graphe complet à sommets pour que toutes les arêtes soient de longueur 1. Par exemple, il faut 2 dimensions pour le graphe complet à 3 sommets représenté par un triangle équilatéral, 3 dimensions pour le graphe complet à 4 sommets représenté par un quadrilatère régulier (figure), etc.
Dit autrement, la dimension du graphe complet coïncide avec la dimension du simplexe associé.

Graphes bipartis complets
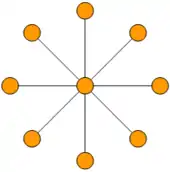
Tous les graphes étoile , pour sommets périphériques, sont de dimension 2 (figure) : ils ont besoin d'un plan pour être tracés avec des arêtes de longueur 1. Les graphes étoile à 1 et 2 sommets périphériques n'ont besoin que d'une droite (dimension 1).
La dimension d'un graphe biparti complet , pour , vaut 3 : sur la figure, on voit comment placer sommets sur un même cercle et les 2 sommets restants sur l'axe de ce cercle. peut quant à lui se tracer avec un losange dans un plan.
La dimension d'un graphe biparti complet général , pour et , vaut 4.
En résumé :
- , selon les valeurs de et de
Dimension et nombre chromatique
Théorème — La dimension de n'importe quel graphe est toujours inférieure ou égale au double de son nombre chromatique :
Dimension euclidienne


La notion de dimension d'un graphe présentée plus haut ne satisfait pas complètement certains auteurs. En effet :
- si deux sommets de sont reliés par une arête, alors leur représentation les place à 1 unité de distance ;
- en revanche, si dans la représentation, deux sommets sont à une unité de distance, ils ne sont pas forcément reliés dans le graphe.
La figure ci-contre montre le problème dans le cas d'un graphe roue à un sommet central et 6 sommets périphériques auquel on a retiré un des rayons. Sa représentation dans le plan admet deux sommets à distance 1, mais qui ne sont pas reliés.
Alexander Soifer définit en 1991 la dimension euclidienne d'un graphe[4]. Avant lui, en 1980, Paul Erdős et Miklós Simonovits l'avaient déjà définie sous le nom de dimension fidèle (faithful dimension)[5]. La dimension euclidienne d'un graphe est le nombre entier tel que dans une représentation classique de dans l'espace à dimensions , deux sommets du graphe sont reliés si et seulement si leurs représentations sont à une distance de 1.
On note cette dimension . Elle est toujours plus élevée que la dimension définie plus haut :
Ainsi, dans l'exemple du graphe roue auquel on a enlevé une arête radiale, si l'on exclut que des sommets non reliés puissent être à une distance de 1, il faut sortir un sommet du plan (illustration).
Dimension euclidienne et degré maximal
Paul Erdős et Miklós Simonovits ont démontré en 1980 le résultat suivant[5] :
Théorème — La dimension euclidienne de n'importe quel graphe est inférieure ou égale au double de son degré maximal plus un :
Notes et références
- Dans la représentation classique d'un graphe, les sommets sont représentés par des points et les arêtes par des segments de droite.
- (en) P. Erdős, F. Harary et W. T. Tutte, « On the dimension of a graph », Mathematika, no 12, , p. 118 à 122 (lire en ligne)
- Le principe de cette preuve est dû à Lenz en 1955 ; il ne l'a pas publiée et on ne la connaît que par Paul Erdős.
- (en) Alexander Soifer, The Mathematical Coloring Book, Springer, (ISBN 978-0-387-74640-1)
- (en) P. Erdős et M. Simonovits, « On the chromatic number of geometric graphs », Ars Comb., no 9, , p. 229 à 246
- Portail de la géométrie