Dimension de Minkowski-Bouligand

Supposons que N(ε) soit le nombre de cases de côté ε nécessaires pour recouvrir l'ensemble. On souhaite que ${\displaystyle N(\epsilon )}$ soit « équivalent, au moins approximativement », à ${\displaystyle c\epsilon ^{-D}}$(${\displaystyle c}$ et la dimension ${\displaystyle D}$ étant des constantes positives[2] ; cf. l'approche didactique de l'article dimension fractale). Pour trouver ${\displaystyle D}$, on prend les logarithmes : ${\displaystyle \log N(\epsilon )\simeq \log c-D\log \epsilon }$. D'où ${\displaystyle D\simeq {\frac {\log N(\epsilon )}{-\log \epsilon }}+{\frac {\log c}{\log \epsilon }}}$. Le second terme disparaît à la limite. Nous pouvons espérer obtenir une définition raisonnable avec ce qui suit[2] :

La dimension de Minkowski est définie par :

${\displaystyle \dim _{\rm {box}}(S):=\lim _{\varepsilon \to 0}{\frac {\log N(\varepsilon )}{\log(1/\varepsilon )}}}$.

Si la limite n'existe pas, alors on parle de dimension supérieure pour la limite supérieure et dimension inférieure pour la limite inférieure. En d'autres termes la dimension de Minkowski n'est bien définie que si ces deux valeurs sont égales. La dimension supérieure est parfois appelée dimension d'entropie, dimension de Kolmogorov ou notée upper box. La limite inférieure est parfois notée lower box.

Les deux sont fortement liées à la dimension de Hausdorff. Dans certains cas, ces trois valeurs sont différentes (voir plus bas pour plus de détails).

Trois types de recouvrements.

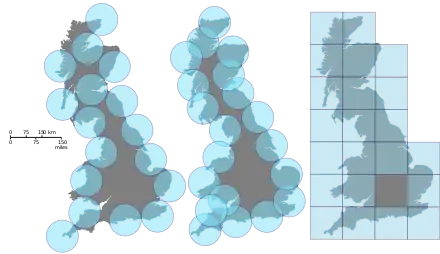
La dimension de Minkowski reste identique pour les différents types de recouvrements pour lesquels N(ε) désigne[3] :

• le nombre de cases de côté ε, sur un réseau carré, nécessaires pour recouvrir l'ensemble (à droite, sur l'illustration) ;
• le plus petit nombre de boules de rayon ε couvrant l'ensemble (au milieu) ;
• le plus petit nombre de cubes de côté ε couvrant l'ensemble ;
• le plus petit nombre d'ensembles de diamètre au plus ε couvrant l'ensemble ;
• le plus grand nombre de boules disjointes de rayon ε centrées sur l'ensemble (à gauche).

Une autre définition équivalente[3] de la dimension de Minkowski considère la façon dont le volume du voisinage de S décroit à mesure que ce voisinage rétrécit. Elle est donnée par la formule :

${\displaystyle \dim _{\text{box}}(S)=n-\lim _{\varepsilon \to 0}{\frac {\log {\text{vol}}(S_{\varepsilon })}{\log \varepsilon }}}$

où, pour tout ${\displaystyle \varepsilon >0}$, l'ensemble ${\displaystyle S_{\varepsilon }}$ est le ε-voisinage de S, c'est-à-dire l'ensemble des points de ${\displaystyle \mathbb {R} ^{n}}$ qui sont à une distance inférieure ou égale à ε de S. Ou, de manière équivalente, ${\displaystyle S_{\varepsilon }}$ est l'union de toutes les boules fermées de rayon ε centrées dans S :

${\displaystyle S_{\varepsilon }=\{x\in \mathbb {R} ^{n}\mid \exists y\in S\quad |x-y|\leq \varepsilon \}}$.

Les deux dimensions (upper et lower box) sont finiment additives, c'est-à-dire que si { A₁, … , A_n } est une collection finie d'ensembles, alors

${\displaystyle \dim _{*{\text{box}}}(A_{1}\cup \dotsb \cup A_{n})=\max\{\dim _{*{\text{box}}}A_{1},\dots ,\dim _{*{\text{box}}}A_{n}\}}$.

Toutefois, cette propriété ne vaut pas pour une collection infinie d'ensembles. Par exemple, la dimension d'un point vaut 0. Mais la dimension de Minkowski des nombres rationnels sur l'intervalle [0, 1] a pour valeur 1.

La dimension de Minkowski peut être vue comme la façon dont on peut recouvrir un ensemble avec de petits objets de même taille alors que la dimension de Hausdorff considère des recouvrements par des petits objets de taille variant, peut-être, de manière très significative. De plus, la dimension de Hausdorff s'appuie sur une mesure, ce qui n'est pas le cas pour la dimension de Minkowski, ce qui occasionne certaines propriétés jugées indésirables[3] (voir ci-dessous).

Malgré cela, la dimension de Minkowski est couramment utilisée pour la mesure d'objets fractals, car la mesure de Hausdorff est difficile à mettre en application.

Les dimensions de Minkowski et de Hausdorff sont égales pour nombre d’ensembles fractals ; ceci est notamment conjecturé[4] pour les ensembles fractals strictement auto-similaires. Par exemple, les dimensions de Hausdorff et de Minkowski de l’ensemble de Cantor sont égales à ${\displaystyle \log(2)/\log(3)}$.

La dimension de Hausdorff et la dimension de Minkowski sont liées par l’inégalité suivante :

${\displaystyle \dim _{\operatorname {Haus} }\leq \dim _{\operatorname {lowerbox} }\leq \dim _{\operatorname {upperbox} }}$.

En général, les inégalités sont strictes. En voici quelques exemples :

Exemple 1: La dimension de Minkowski supérieure peut être plus grande que la dimension inférieure si l’ensemble fractal a un comportement différent à différentes échelles. Par exemple, prenons l’intervalle [0,1] et examinons l’ensemble des nombres satisfaisant les conditions suivantes :

• pour tout ${\displaystyle n}$, toutes les décimales entre la ${\displaystyle 2^{2n}}$-ième décimale et la ${\displaystyle (2^{2n+1}-1)}$-ième décimale valent zéro ;
• les décimales entre la ${\displaystyle 2^{2n+1}}$ et ${\displaystyle 2^{2n+2}-1}$ peuvent prendre n’importe quelle valeur.

Cette fractale a pour dimension supérieure 2/3 et pour dimension inférieure 1/3, un résultat qui peut être vérifié aisément en calculant N(ε) pour ${\displaystyle \varepsilon =10^{-2^{n}}}$ et en remarquant que leur valeurs se comportent différemment pour n pair et impair. La dimension de Hausdorff, pour le même ensemble, vaut 0.

Exemple 2 : L’ensemble ${\displaystyle \mathbb {Q} \cap \left[0,1\right]}$ des rationnels compris entre 0 et 1, un ensemble dénombrable avec ${\displaystyle \textstyle {\dim _{\operatorname {Haus} }=0}}$, a pour dimension de Minkowski ${\displaystyle \textstyle {\dim _{\operatorname {box} }=1}}$ parce que son adhérence, ${\displaystyle \left[0,1\right]}$, a pour dimension 1.

Exemple 3 : La dimension de Minkowski manque également de propriétés de stabilité que l’on attendrait d’une dimension. Par exemple, on s’attendrait à ce que l’ajout d’un ensemble dénombrable n’ait aucun effet sur la valeur de la dimension. Cette propriété ne fonctionne pas pour la dimension de Minkowski. Ainsi :

${\displaystyle \dim _{\operatorname {box} }\left\{0,1,{\frac {1}{2}},{\frac {1}{3}},{\frac {1}{4}},\ldots \right\}={\frac {1}{2}}.}$