Dérivée directionnelle

Soient E un espace vectoriel normé, U un ouvert de E, f une fonction définie sur U à valeurs dans un espace vectoriel normé F (ou plus généralement, un espace vectoriel topologique séparé). On donnera la qualification de points aux éléments de U et de vecteurs aux éléments de E, les raisons en seront détaillées au-dessous. Soient également u un point de U et h un vecteur de E.

La dérivée de f au point u suivant le vecteur h est, si elle existe, la dérivée en 0 de la fonction de la variable réelle ${\displaystyle t\mapsto f(u+th)}$ :

${\displaystyle D_{h}f(u)=\lim \limits _{t\to 0}{\frac {f(u+th)-f(u)}{t}}.}$

Si h est le vecteur nul, cette limite existe toujours et a une valeur nulle. On pourra supposer que h n'est pas le vecteur nul dans ce qui suit.

Lorsque l'espace E est de dimension finie n et muni d'une base, la fonction f peut être vue comme une fonction de n variables réelles, et le calcul des dérivées directionnelles suivant les vecteurs de base correspond au calcul des dérivées partielles de f :

${\displaystyle D_{e_{i}}f(u)={\frac {\partial f}{\partial x_{i}}}(u).}$

Si on remplace h par un vecteur colinéaire αh, le calcul de dérivée est identique à la multiplication par le facteur α près :

${\displaystyle D_{\alpha h}f(u)=\alpha D_{h}f(u).}$

Ainsi, lorsqu'il existe en un point une dérivée suivant un vecteur, il en existe une suivant tout vecteur de même direction, mais la valeur de cette dérivée directionnelle dépend du choix du vecteur. On parlera de dérivée directionnelle de f au point u dans la direction de h lorsque le vecteur h est unitaire[1].

En revanche il n'y a pas de raison a priori d'observer un résultat particulier lorsqu'on somme deux vecteurs h et h'.

La définition ci-dessus définit la dérivée dans la direction de h lorsque le vecteur h est unitaire.

Certains auteurs définissent^{[réf. souhaitée]} la dérivée dans la direction d'un vecteur quelconque ${\displaystyle v\neq 0}$ par :

${\displaystyle \nabla _{v}f(u):=\lim _{s\to 0}{\frac {f(u+sv)-f(u)}{s\left\|v\right\|}}.}$

Le lien avec la définition précédente est donc : ${\displaystyle \nabla _{v}f(u)=D_{h}f(u)}$ pour ${\displaystyle h={\frac {v}{\left\|v\right\|}}}$.

Intuitivement, la dérivée directionnelle de ${\displaystyle f}$ au point u représente le taux de changement de ${\displaystyle f}$, mesuré selon la direction ${\displaystyle v}$, par rapport au temps, lorsqu'on passe par le point u.

Si la fonction f est différentiable au point u, alors elle admet des dérivées en ce point dans la direction de tout vecteur. Cette dérivée se calcule à partir de l'application différentielle en u (notée df(u)) par application de la formule

${\displaystyle D_{h}f(u)=({\rm {d}}f(u))(h),}$

si bien que cette fois, le résultat est linéaire en h. Notamment,

${\displaystyle D_{h+h'}f(u)=D_{h}f(u)+D_{h'}f(u).}$

Enfin, si E est un espace vectoriel de dimension finie n muni d'une base, il est possible de calculer toutes les dérivées directionnelles en termes de dérivées partielles

${\displaystyle D_{h}f(u)=\sum _{i=1}^{n}h_{i}{\frac {\partial f}{\partial x_{i}}}(u).}$

En général, la réciproque est fausse : le fait qu'une application présente des dérivées en u dans toutes les directions n'assure pas sa différentiabilité, ni même sa continuité. Cependant, la réciproque est vraie si la fonction est définie sur un espace vectoriel de dimension finie n, est à valeurs réelles et est convexe : il suffit qu'elle ait des dérivées partielles suivant n vecteurs linéairement indépendants pour qu'elle soit différentiable (au sens de Fréchet).

Si E est un espace vectoriel euclidien et f une application différentiable à valeurs réelles, il est possible d'utiliser le gradient de f pour exprimer la dérivée directionnelle

${\displaystyle D_{h}f(u)=\langle \nabla f(u)|h\rangle .}$

Lorsque f présente un extremum local en un point d'un ouvert, le gradient est nul en ce point (pour une étude plus détaillée voir point critique), ainsi que toutes les dérivées directionnelles.

La dérivée de la fonction f au point u dans la direction du vecteur h se calcule comme la dérivée en 0 de la fonction d'une seule variable réelle g(t) = f(u + th). Cette dernière s'interprète comme la restriction de f à la droite affine passant par u et dirigée par h.

L'angle α entre la tangente en A' et l'horizontale sera maximal si le plan de coupe contient la direction du gradient en A.

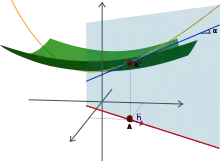
Si l'on associe à la fonction ${\displaystyle f:U\subset \mathbb {R} ^{2}\to \mathbb {R} }$ la surface (S) d'équation cartésienne z = f(x, y), la notion de dérivée dans la direction d'un vecteur ${\displaystyle h=(h_{1},h_{2})~}$ unitaire en un point ${\displaystyle A=(x_{0},y_{0})~}$ de U peut être interprétée ainsi : le plan vertical contenant la droite passant par A et dirigée par h coupe la surface (S) selon la courbe paramétrée (C) :

${\displaystyle t\mapsto M(t)={\begin{cases}x_{0}+th_{1}\\y_{0}+th_{2}\\f(x_{0}+th_{1},y_{0}+th_{2}).\end{cases}}}$

La fonction M est dérivable en 0 si et seulement si f admet en A une dérivée dans la direction de h ; dans ce cas, il existe une tangente au point ${\displaystyle A'=M(0)}$ — qui est le point de (S) à la verticale de A — et ${\displaystyle D_{h}f(A)}$ est la composante verticale du vecteur directeur de cette tangente.

Si f est différentiable en A, l'inégalité de Cauchy-Schwarz permet d'écrire (avec toujours h unitaire)

${\displaystyle -\|\nabla f(A)\|\leqslant D_{h}f(A)=\langle \nabla f(A)|h\rangle \leqslant \|\nabla f(A)\|}$

avec égalité si (et seulement si) h est colinéaire au gradient de f en A.

La pente de la tangente est donc maximale en choisissant la direction du gradient, ce qui est à la base des méthodes de descente dans les problèmes de minimisation[2].

Soient E un espace vectoriel, F un espace vectoriel normé et ${\displaystyle f:E\to F}$ une fonction. On dit que f est directionnellement dérivable au sens de Dini en ${\displaystyle x\in E}$ dans la direction ${\displaystyle d\in E}$ si la limite dans la définition de ${\displaystyle f'_{_{D}}(x;d)}$ ci-dessous existe dans F :

Soient E et F deux espaces vectoriels normés. Une fonction ${\displaystyle f:E\to F}$ est dite Gateaux-différentiable[3] en ${\displaystyle x\in E}$ si

1. la dérivée directionnelle ${\displaystyle f'_{D}(x;d)}$ existe quel que soit ${\displaystyle d\in E}$,
2. l'application ${\displaystyle D_{G}f(x):d\in E\mapsto f'_{_{D}}(x;d)\in F}$ est linéaire continue.

On dit que f est continûment Gateaux-différentiable en ${\displaystyle x\in E}$ si f est Gateaux-différentiable dans un voisinage V de x et ${\displaystyle D_{G}f:V\to {\mathcal {L}}(E,F)}$ est continue en x ; on a noté ${\displaystyle {\mathcal {L}}(E,F)}$ l'ensemble des opérateurs linéaires continus de E dans F, muni de sa norme canonique.

En analyse convexe ou non lisse, on utilise une notion de dérivée directionnelle, qui est essentiellement celle de Dini, mais qui accepte que les fonctions prennent leurs valeurs dans la droite réelle achevée ${\displaystyle {\overline {\mathbb {R} }}:=\mathbb {R} \cup \{-\infty ,+\infty \}}$. Les dérivées directionnelles peuvent elles-mêmes prendre leurs valeurs dans ${\displaystyle {\overline {\mathbb {R} }}}$. Voici cette définition.

Soient E un espace vectoriel et ${\displaystyle f:E\to {\overline {\mathbb {R} }}}$ une fonction. On dit que ${\displaystyle f}$ est directionnellement dérivable en ${\displaystyle x\in E}$ dans la direction ${\displaystyle d\in E}$ si la limite dans la définition de ${\displaystyle f'(x;d)}$ ci-dessous existe dans ${\displaystyle {\overline {\mathbb {R} }}}$ :

Cette définition est motivée par le résultat suivant qui assure la dérivabilité directionnelle des fonctions convexes, dans toutes les directions. On y a noté

• ${\displaystyle \operatorname {dom} \,f:=\{x\in E\mid f(x)<+\infty \}}$ le domaine effectif de ${\displaystyle f}$ ;
• ${\displaystyle \operatorname {aff} {(C)}}$ l'enveloppe affine d'une partie ${\displaystyle C\subset E}$ ;
• ${\displaystyle \operatorname {ir} {(C)}}$ l'intérieur relatif d'un convexe ${\displaystyle C\subset E}$.

Ce résultat est utilisé pour définir le sous-différentiel d'une fonction convexe.

Soient E un espace vectoriel, F un espace vectoriel normé et ${\displaystyle f:E\to F}$ une fonction. On dit que f est directionnellement dérivable au sens de Hadamard en ${\displaystyle x\in E}$ dans la direction ${\displaystyle d\in E}$ si la limite dans la définition de ${\displaystyle f'_{H}(x;d)}$ ci-dessous existe dans F :

La présentation ci-dessous se fonde sur l'ouvrage de Clarke (1983)[4].

Soient E un espace de Banach et ${\displaystyle f:E\to \mathbb {R} }$ une fonction. La dérivée directionnelle de Clarke de f en x dans la direction ${\displaystyle d\in E}$ est notée ${\displaystyle f^{\circ }(x;d)}$ et définie par

Cette dérivée ne présuppose pas l'existence d'une limite ; elle existe toujours, mais elle peut cependant prendre une valeur infinie. L'utilité de cette dérivée directionnelle repose sur les propriétés suivantes.

La dérivée directionnelle de Clarke est utilisée pour définir le sous-différentiel de Clarke d'une fonction localement lipschitzienne.

Le concept de différentiabilité naturellement relié à la dérivée directionnelle de Clarke est celui de différentiabilité stricte, que l'on trouve chez Bourbaki. La fonction considérée peut ici être à valeurs dans un espace vectoriel, pas seulement dans ${\displaystyle \mathbb {R} }$ ; nous avons marqué ce fait en la désignant par F, plutôt que f.

Soient ${\displaystyle \mathbb {E} }$ et ${\displaystyle \mathbb {F} }$ deux espaces de Banach. Une fonction ${\displaystyle F:\mathbb {E} \to \mathbb {F} }$ est dite strictement différentiable en ${\displaystyle x\in \mathbb {E} }$ si l'application

est linéaire continue et la limite est uniforme pour d dans un compact arbitraire.

Le résultat suivant apporte deux informations : d'une part, une fonction strictement différentiable en un point est nécessairement lipschitzienne dans un voisinage de ce point et, d'autre part, pour une fonction lipschitzienne, la différentiabilité stricte en un point est assurée sans que l'on ait besoin de vérifier la condition d'uniforme convergence pour des directions dans un compact.

Une fonction continûment Gateaux-différentiable est strictement différentiable.

Soit f une fonction numérique sur une variété différentielle M. Avec une définition analogue à la précédente, il est loisible d'introduire la dérivée de f en un point m de M et dans la direction d'un vecteur tangent h en m à la variété. Comme la notion de droite dirigée par h n'a plus de sens, il faut la remplacer par une courbe passant par m et de vecteur tangent h en ce point.

Soit γ une courbe tracée sur M, continûment dérivable, vérifiant γ(0) = m et γ'(0) = h. Si la dérivée en 0 de f∘γ existe, elle est appelée dérivée de f au point m dans la direction de h. On montre en effet que cette définition ne dépend pas de la courbe γ convenable choisie.

Si X est un champ de vecteurs ${\displaystyle {\mathcal {C}}^{\infty }}$ sur la variété M et si f est une fonction numérique ${\displaystyle {\mathcal {C}}^{\infty }}$ sur M, il est possible de calculer les dérivées partielles de f en chaque point p selon le vecteur X(p). La fonction obtenue en considérant toutes ces dérivées est notée ${\displaystyle X\cdot f={\mathcal {L}}_{X}f}$ et est appelée dérivée de Lie de f par X.

Pour calculer la dérivée de Lie de f, il est notamment possible de prendre pour courbes tangentes aux vecteurs X(p) les courbes intégrales du champ de vecteurs. La généralisation de ce point de vue à la dérivation des champs de vecteurs, formes différentielles et tenseurs est décrite à l'article « Dérivée de Lie ».