Diagrammes de Tanabe-Sugano

Les diagrammes de Tanabe–Sugano sont utilisés en chimie de coordination pour prédire l'absorption dans le spectre électromagnétique UV, visible et IR d'un complexe de coordination. Le résultat de l'analyse d'un diagramme de Tanabe–Sugano d'un complexe métallique peut aussi être comparé aux données spectroscopiques expérimentales. Ces diagrammes sont utiles d'un point de vue qualitatif et peuvent être utilisés pour approximer la valeur de 10Dq, l'énergie d'éclatement du champ des ligands. Ils peuvent être utilisés aussi bien pour les complexes à bas spin qu'à haut spin, contrairement aux Diagrammes d'Orgel (en) qui ne s'appliquent qu'aux complexes à haut spin. Les diagrammes de Tanabe–Sugano peuvent aussi être utilisés pour prédire la force du champ de ligand nécessaire pour causer une transition de haut spin à bas spin.

Dans un diagramme de Tanabe–Sugano, l'état fondamental est utilisé comme une référence constante, contrairement aux diagrammes d'Orgel. L'énergie de l'état fondamental est prise égale à zéro pour toutes les forces de champ, et les énergies des autres termes et de leurs composants sont tracées par rapport à l'état fondamental.

Historique

Avant que Yukito Tanabe et Satoru Sugano publient leur article intitulé On the absorption spectra of complex ions, les états électroniques excités des complexes des ions métalliques étaient mal connus. Ils utilisèrent la théorie du champ cristallin de Hans Bethe et les combinaisons d'intégrales de Slater de Giulio Racah[1] (ce qu'on appelle aujourd'hui paramètre de Racah) pour expliquer les spectres d'absorption des complexes octaédriques d'une façon plus quantitative que ce qui avait été fait jusque là[2]. Après de nombreuses expériences de spectroscopie, ils estimèrent les valeurs de deux des paramètres de Racah, B et C, pour chacune des configurations électroniques des électrons d à partir des tendances dans les spectres d'absorption des complexes isoélectroniques des métaux de transition de la première période. C'est le tracé des énergies calculées pour les états électroniques de chaque configuration électronique qu'on appelle maintenant diagrammes de Tanabe-Sugano[3],[4].

Paramètres

L'axe des abscisses d'un diagramme de Tanabe–Sugano représente le paramètre d'éclatement du champ des ligands, Dq, ou Δ, divisé par le paramètre de Racah B. L'axe des ordonnées représente l'énergie E, là encore divisée par B. Il existe trois paramètres de Racah, A, B, et C, qui décrivent différents aspects de la répulsion interélectronique. A est une moyenne de la répulsion interélectronique totale. B et C correspondent aux répulsions individuelles entre électrons d. A est constante pour une configuration des électrons d, et n'est pas nécessaire pour calculer les énergies relatives, d'où son absence de l'étude des complexes ioniques par Tanabe et Sugano. C ne sert que dans certains cas. B est le plus important des paramètres de Racah dans ce cas[5]. Chaque ligne correspond à un état électronique. La courbure de certaines lignes est due au mélange de termes de même symétrie. Bien que les transitions électroniques soient "permises" seulement si la multiplicité de spin demeure la même (i.e. si les électrons ne passent pas d'un nombre quantique magnétique de spin +1/2 à -1/2 ou l'inverse quand on passe d'un niveau d'énergie à un autre), les niveaux d'énergie pour les états électroniques "interdits de spin" sont inclus dans les diagrammes, bien qu'ils ne soient pas inclus dans les diagrammes d'Orgel[6]. À chaque état on attribue son étiquette de symétrie (par exemple A1g, T2g, etc.), mais les indices "g" et "u" sont généralement omis car il est admis que tous les états sont gerade. Les étiquettes de chaque état sont habituellement écrites du côté droit de la table, bien que pour les diagrammes plus compliqués (par exemple d6) elles puissent être écrites ailleurs pour faciliter la lecture. Les symboles des termes spectroscopiques (par exemple 3P, 1S, etc.) pour un ion libre dn spécifique sont listés, par ordre d'énergie croissante, sur l'axe des ordonnées du diagramme. L'ordre relatif des énergies est déterminé en utilisant la règle de Hund. Pour un complexe octaédrique, les termes spectroscopiques de l'ion libre sphérique s'éclatent comme indiqué ci-dessous[7] :

Éclatement des Termes Spectroscopiques de la Symétrie Sphérique à la Symétrie Octaédrique
TermeDegénerescenceÉtats en champ octaédrique
S1A1g
P3T1g
D5Eg + T2g
F7A2g + T1g + T2g
G9A1g + Eg + T1g + T2g
H11Eg + T1g + T1g + T2g
I13A1g + A2g + Eg + T1g + T2g + T2g

Certains diagrammes de Tanabe–Sugano (d4, d5, d6, et d7) ont aussi une ligne verticale tracée pour une valeur spécifique de Dq/B, qui correspond à une discontinuité dans les pentes des niveaux d'énergie des états excités. Ce "pincement" des lignes apparaît lorsque l'énergie d'appariement des spins, P, est égale à l'énergie d'éclatement du champ des ligands, Dq. Les complexes à gauche de cette ligne (pour des valeurs basses de Dq/B) sont haut-spin, alors que les complexes à droite (hautes valeurs de Dq/B) sont bas-spin. Il n'y a pas de désignation bas-spin ou haut-spin pour d2, d3, ou d8[8].

Diagrammes de Tanabe-Sugano

Les sept diagrammes de Tanabe–Sugano pour les complexes octaédriques sont représentés ci-dessous[5],[9],[10].

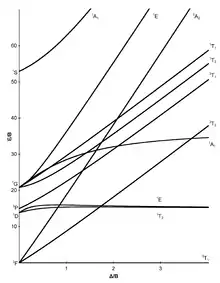configuration électronique d2
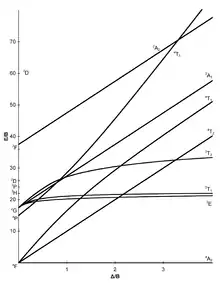configuration électronique d3
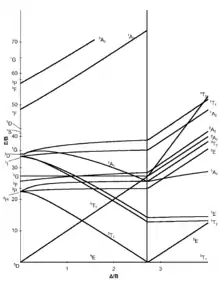configuration électronique d4
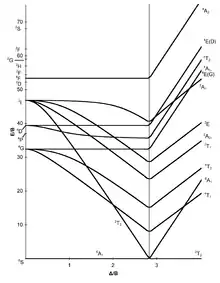configuration électronique d5
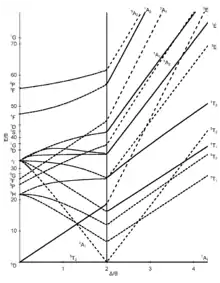configuration électronique d6
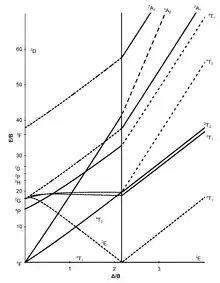configuration électronique d7
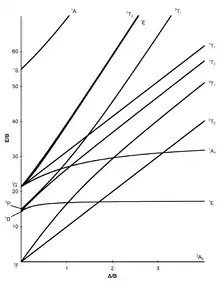configuration électronique d8


Diagrammes inutiles : d1, d9 et d10

d1

Il n'y a pas de répulsion interélectronique dans un complexe d1 puisqu'il n'y a qu'un électron célibataire : celui-ci est donc dans une orbitale t2g de l'état fondamental. Un complexe métallique octaédrique d1, comme [Ti(H2O)6]3+, présente une seule bande d'absorption dans son spectre UV-vis[5]. Le terme spectroscopique pour d1 est 2D, qui se sépare en états 2T2g et 2Eg. L'ensemble d'orbitales t2g contient l'électron célibataire et a un niveau d'énergie 2T2g de -4Dq. Quand cet électron est promu dans une orbitale eg, il passe dans l'état excité 2Eg dont l'énergie est +6Dq. Ceci est en accord avec la présence d'une seule bande dans son spectre d'absorption UV-Vis. L'épaulement proéminent de cette bande d'absorption est dû à une distorsion Jahn-Teller qui lève la dégénérescence des deux états 2Eg. Cependant, comme ces deux transitions se recouvrent dans le spectre UV-vis, cette transition de 2T2g à 2Eg ne nécessite pas un diagramme de Tanabe–Sugano.

d9

De la même manière que pour les complexes métalliques d1, les complexes métalliques d9 ont un terme spectroscopique 2D. La transition se fait de la configuration (t2g)6(eg)3 (état 2Eg) vers la configuration (t2g)5(eg)4 (état 2T2g). Ceci peut aussi être décrit comme le mouvement d'un "trou" positif depuis une orbitale eg vers une orbitale t2g. Le signe de Dq est l'opposé de celui pour d1, avec un état fondamental 2Eg et un état excité 2T2g. Comme dans le cas d1, les complexes octaédriques d9 ne nécessitent pas de diagramme de Tanabe–Sugano pour prédire leur spectre d'absorption.

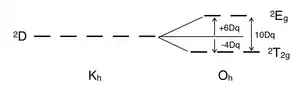Éclatement du terme 2D par un champ cristallin octaédrique
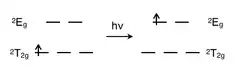Transition électronique de l'état fondamental 2T2g vers l'état excité 2Eg pour une configuration électronique d1
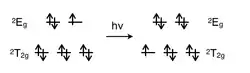Transition électronique de l'état fondamental vers l'état excité pour une configuration électronique d9

d10

Il n'y a pas de transitions électroniques d-d dans les complexes métalliques d10 puisque les orbitales d sont complètement remplies. Par conséquent, les bandes d'absorption UV-vis ne sont pas observées et il n'y a pas de diagramme de Tanabe–Sugano.

Diagrammes pour la symétrie tétraédrique

Les diagrammes de Tanabe–Sugano Tétraédriques ne figurent généralement pas dans les livres car le diagramme pour un dn tétraédrique sera semblable à celui d'un d(10-n) octaédrique, en se souvenant que le ΔT pour les complexes tétraédriques est approximativement 4/9 de ΔO pour un complexe octaédrique. Une conséquence de la valeur bien plus petite de ΔT est que (presque) tous les complexes tétraédriques sont haut spin et par conséquent le changement de l'état fondamental vu sur l'axe X pour les diagrammes d4-d7 octaédriques n'est plus nécessaire pour interpréter les spectres des complexes tétraédriques.

Avantages par rapport aux diagrammes d'Orgel

Dans un Diagramme d'Orgel (en), l'amplitude de l'énergie d'éclatement imposée par les ligands sur les orbitales d, lorsqu'un ion libre approche d'un champ de ligands, est comparée à la répulsion électronique, les deux étant suffisantes pour déterminer la répartition des électrons. Cependant, si l'énergie d'éclatement du champ de ligand 10Dq est plus grande que la répulsion électronique, alors le diagramme Orgel ne permet plus de déterminer la répartition des électrons. Dans ce cas, les diagrammes d'Orgel sont restreints seulement aux complexes haut spin[6].

Les diagrammes de Tanabe–Sugano n'ont pas cette restriction, et peuvent être appliqués dans les situations où 10Dq est significativement plus grand que la répulsion électronique. Ainsi, les diagrammes de Tanabe–Sugano sont utilisés pour déterminer la répartition des électrons pour les complexes métalliques haut spin et bas spin. Pourtant, ils sont limités dans le sens où ils n'ont qu'une signification qualitative. Malgré cela, les diagrammes de Tanabe–Sugano sont utiles pour interpréter les spectres UV-vis et déterminer la valeur de 10Dq[6].

Applications comme outil quantitatif

Dans un champ des ligands centrosymétrique, comme c'est le cas dans les complexes octaédriques des métaux de transitions, l'arrangement des électrons dans les orbitales d n'est pas seulement limité par l'énergie de répulsion électronique, mais il est aussi relié à l'éclatement des orbitales par le champ des ligands. Ceci conduit à beaucoup plus d'états de configuration électronique que dans le cas de l'ion libre. L'énergie relative de la répulsion électronique et de l'éclatement définit les états haut-spin bas-spin.

En considérant à la fois les champs des ligands forts et faibles, un diagramme de Tanabe–Sugano montre l'éclatement de l'énergie des termes spectroscopiques avec l'augmentation de la force du champ des ligands. Il est possible de comprendre comment l'énergie des différents états de configuration est distribuée pour certaines forces de ligands. La restriction de la règle de sélection de spin rend encore plus facile la prédiction des transitions possibles et de leur intensité relative. Bien qu'ils soient qualitatifs, les diagrammes de Tanabe–Sugano sont des outils très utiles pour analyser les spectres UV-vis : ils sont utilisés pour attribuer les bandes et calculer les valeurs de Dq pour l'éclatement d'un champ des ligands[11],[12].

Exemples
Spectre d'absorption de [Mn(H2O)6]2+.

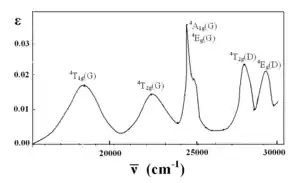
Hexahydrate de manganèse(II)

Dans le complexe métallique [Mn(H2O)6]2+, le manganèse est au degré d'oxydation +2, donc c'est un ion d5. H2O est un ligand à champ faible (cf. spectre ci-contre), et d'après le diagramme de Tanabe–Sugano pour les ions d5, l'état fondamental est 6A1. On remarque qu'il n'y a pas de sextuplet de multiplicité de spin dans aucun état excité, par conséquent les transitions de cet état fondamental sont interdites de spin et les intensités des bandes devraient être basses. Dans le spectre, seules des bandes de très basse intensité sont observées (faibles valeurs de coefficient d'absorption molaire(ε) sur l'axe y)[11].

Spectre d'absorption de [Co(H2O)6]2+.

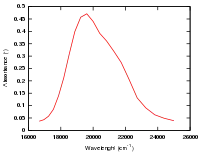
Hexahydrate de cobalt(II)

Un autre exemple : [Co(H2O)6]2+[12]. On remarque que le ligand est le même que dans l'exemple précédent. Puisque l'ion cobalt est au degré d'oxydation +2, c'est un ion d7. Du côté haut-spin du diagramme de Tanabe-Sugano (côté gauche), l'état fondamental est 4T1(F), et la multiplicité de spin est un quadruplet. Le diagramme montre qu'il y a trois états excités quadruplets : 4T2, 4A2, et 4T1(P). À partir du diagramme on peut prédire qu'il y a trois transitions autorisées de spin. Cependant, le spectre de [Co(H2O)6]2+ ne présente pas trois pics distincts correspondant aux trois états excités prédits. À la place, le spectre présente un pic large (cf. spectre ci-contre). Selon le diagramme de Tanabe-Sugano, la plus basse énergie de transition est de 4T1 à 4T2, qui se situe dans le proche IR et n'est pas observée sur le spectre visible. Le pic principal est l'énergie de transition de 4T1(F) à 4T1(P), et l'énergie de transition légèrement supérieure (l'épaulement) est prédite comme de 4T1 à 4A2. La petite différence d'énergie conduit au recouvrement des deux pics, ce qui explique le pic large observé dans le spectre visible.

Comment déterminer B et ΔO
diagramme de Tanabe-Sugano d2

Pour le complexe d2 [V(H2O)6]3+, on observe deux bandes avec des maxima à environ 17500 et 26000 cm−1.[réf. nécessaire] Le rapport entre les énergies de bandes expérimentales est E(ν2)/E(ν1) = 1,49. Il y a trois transitions possibles attendues, qui sont : ν1 : 3T1g→3T2g, ν2 :3T1g→3T1g(P), et ν3 : 3T1g→3A2g. Sur ces trois transitions possibles, seules deux sont observées, donc la transition non-observée doit être déterminée.

ΔO / B =10203040
Hauteur E(ν1)/B 10192837
Hauteur E(ν2)/B 23334252
Hauteur E(ν3)/B 19385675
Rapport E(ν3)/E(ν1) 1.92.02.02.0
Rapport E(ν2)/E(ν1) 2.31.731.51.4

On remplit un tableau comme celui à droite en trouvant les hauteurs correspondantes (E/B) des états de symétrie pour certaines valeurs de ΔO / B. Puis on trouve le rapport de ces valeurs (E(ν2)/E(ν1) et E(ν3)/E(ν1)). On remarque que le rapport de E(ν3)/E(ν1) ne contient pas le rapport calculé pour les énergies de bandes expérimentales, donc on peut déterminer que la bande 3T1g→3A2g n'est pas observée. On utilise les rapports pour E(ν2)/E(ν1) et les valeurs de ΔO / B pour tracer une droite avec E(ν2)/E(ν1) comme ordonnée et ΔO/B comme abscisse. En utilisant cette droite, il est possible de déterminer la valeur de ΔO / B pour le rapport expérimental. (ΔO / B = 31 pour un rapport de 1,49 dans le tableau de cet exemple).

On trouve ensuite sur le diagramme de Tanabe-Sugano où ΔO / B = 31 pour 3T1g→3T2g et 3T1g→3T1g(P). Pour 3T2g, E(ν1) / B = 27 et pour 3T1g(P), E(ν2) / B = 43.

Le Paramètre de Racah peut être trouvé en calculant B à partir de E(ν2) et E(ν1). Pour 3T1g(P), B = 26000 cm−1/43 = 604 cm−1. Pour 3T2g, B = 17500 cm−1/ 27 = 648 cm−1. À partir de la valeur moyenne du Paramètre de Racah, le paramètre d'éclatement du champ des ligands (ΔO) peut être trouvé. Si ΔO / B = 31 et B = 625 cm−1, alors ΔO = 19375 cm−1.

Voir aussi

Source de la traduction

Références
  1. Giulio Racah, « Theory of complex spectra II », Physical Review, vol. 62, nos 9–10,‎ , p. 438–462 (DOI 10.1103/PhysRev.62.438, Bibcode 1942PhRv...62..438R)
  2. Yukito Tanabe et Satoru Sugano, « On the absorption spectra of complex ions I », Journal of the Physical Society of Japan, vol. 9, no 5,‎ , p. 753–766 (DOI 10.1143/JPSJ.9.753)
  3. Yukito Tanabe et Satoru Sugano, « On the absorption spectra of complex ions II », Journal of the Physical Society of Japan, vol. 9, no 5,‎ , p. 766–779 (DOI 10.1143/JPSJ.9.766)
  4. Yukito Tanabe et Satoru Sugano, « On the absorption spectra of complex ions III », Journal of the Physical Society of Japan, vol. 11, no 8,‎ , p. 864–877 (DOI 10.1143/JPSJ.11.864)
  5. (en) Peter Atkins, Tina Overton, Jonathan Rourke, Mark Weller, Fraser Armstrong, Paul Salvador, Michael Hagerman, Thomas Spiro et Edward Stiefel, Shriver & Atkins Inorganic Chemistry, New York, W.H. Freeman and Company, , 4th éd., 478–483 p. (ISBN 0-7167-4878-9)
  6. (en) Bodie Douglas, Darl McDaniel et John Alexander, Concepts and Models of Inorganic Chemistry, New York, John Wiley & Sons, , 3rd éd., 1000 p. (ISBN 0-471-62978-2)
  7. (en) F. Albert Cotton, Geoffrey Wilkinson et Paul L. Gaus, Basic Inorganic Chemistry, New York, John Wiley & Sons, , 3rd éd., 838 p. (ISBN 0-471-50532-3)
  8. (en) Daniel C. Harris et Michael D. Bertolucci, Symmetry and Spectroscopy : An Introduction to Vibrational and Electronic Spectroscopy, New York, Dover Publications, Inc., , 550 p. (ISBN 978-0-486-66144-5, lire en ligne)
  9. Robert John Lancashire, « Interpretation of the spectra of first-row transition metal complexes », ACS Division of Chemical Education, cONFCHEM,‎ 4–10 june 1999 (lire en ligne)
  10. Robert John Lancashire, « Tanabe-Sugano diagrams via spreadsheets », (consulté le )
  11. Chr Klixbüll Jørgensen, Carl-Henric De Verdier, John Glomset et Nils Andreas Sörensen, « Studies of absorption spectra IV: Some new transition group bands of low intensity », Acta Chem. Scand., vol. 8, no 9,‎ , p. 1502–1512 (DOI 10.3891/acta.chem.scand.08-1502)
  12. Chr Klixbüll Jørgensen, Carl-Henric De Verdier, John Glomset et Nils Andreas Sörensen, « Studies of absorption spectra III: Absorption Bands as Gaussian Error Curves », Acta Chem. Scand., vol. 8, no 9,‎ , p. 1495–1501 (DOI 10.3891/acta.chem.scand.08-1495)
  • Portail de la chimie
  • Portail de la physique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.