Dynamique des cycles

Comme toutes les masses, le cycliste et tous les éléments du vélo sont attirés vers le sol par la gravité. L'attraction gravitationnelle entre les éléments eux-mêmes est négligeable au regard des autres forces en cause et peut être ignorée.

Au point de contact de chaque pneu avec le sol se manifestent des forces de réaction du sol, qui ont une composante horizontale et une composante verticale. La composante verticale contrebalance essentiellement la force gravitationnelle, mais varie aussi avec le freinage et l'accélération. Pour plus de détails, voir la partie sur la stabilité longitudinale ci-dessous. La composante horizontale est due au frottement entre les roues et le sol et inclut la résistance à la rotation. Elle est une réaction aux forces de propulsion, de freinage et de virage.

Les forces de virage sont provoquées par les manœuvres visant à assurer l'équilibre du vélo en plus du simple changement de direction. Elles peuvent être interprétées comme des forces centrifuges dans le référentiel en accélération du vélo et du cycliste, ou simplement comme une inertie dans un référentiel galiléen stationnaire, et non comme des forces.

Les forces gyroscopiques qui agissent sur les parties rotatives comme les roues, le pédalier ou la transmission sont également dues à l'inertie de ces éléments. Ce sujet est plus amplement développé dans la partie sur les effets gyroscopiques ci-dessous.

Les forces aérodynamiques dues à l'atmosphère sont essentiellement des forces de traînée, mais peuvent aussi prendre la forme de vents de côté. Pour une bicyclette à vitesse normale en plat, la traînée aérodynamique est la plus importante force résistant au mouvement du vélo vers l'avant[5].

Les forces internes au système sont causées principalement par le cycliste et les frottements. Le cycliste peut imprimer des couples entre le mécanisme de direction (fourche avant, guidon, roue avant) et le cadre, et entre le cycliste lui-même et le cadre. Des forces de frottements se produisent entre toutes les parties du vélo qui se déplacent l'une contre l'autre : dans les moyeux, dans la transmission, entre le mécanisme de direction et le cadre , etc. De nombreux vélos ont des suspensions avant et arrière, et certaines motos ont un amortisseur de direction, afin de dissiper toute forme d'énergie cinétique indésirable.

Le cycliste transmet du couple au guidon afin de tourner la roue avant, ce qui permet de contrôler l'inclinaison et de préserver l'équilibre. À une vitesse élevée, même un angle de direction faible provoque un déplacement latéral rapide des points de contact au sol ; à une vitesse plus faible, il faut utiliser des angles de direction plus grands pour obtenir le même effet aussi rapidement. De ce fait, il est généralement plus aisé de maintenir l'équilibre à vitesse élevée[6].

Plus le centre de gravité combiné du vélo et du cycliste se trouve à l'avant (proche de la roue avant), moins la roue avant nécessite de correction latérale pour conserver l'équilibre. À l'inverse, plus le centre de gravité se trouve à l'arrière (proche de la roue arrière), plus la roue avant doit appliquer de correction latérale, ou plus le vélo doit avancer, pour regagner l'équilibre. Ce phénomène peut être observé particulièrement sur les vélos couchés et les choppers, dont les roues sont particulièrement écartées. Il peut aussi s'avérer important sur les routières qui transportent un chargement important au-dessus, ou même derrière la roue arrière[7].

Les vélos sont également des exemples de pendules inversés. Un vélo de grande taille, avec un centre de gravité élevé, est plus facile à maintenir en équilibre qu'un vélo plus petit parce qu'il s'inclinera plus lentement[8].

À l'arrêt, un cycliste peut avoir l'impression inverse : un vélo plus lourd demande plus d'effort pour être maintenu droit qu'un vélo de taille identique mais dont le centre de gravité est plus bas. C'est un exemple de levier vertical de seconde classe. Une force faible appliquée à l'extrémité du levier (le siège ou le guidon pour un vélo) déplace plus facilement une masse importante si celle-ci est plus proche du point d'appui, au contact entre les pneus et le sol. C'est pourquoi il est conseillé aux cyclotouristes de transporter leur chargement bas sur leur vélo, notamment en laissant pendre leurs sacs de part et d'autre de leur porte-bagages[9].

Caractéristiques géométriques d'un vélo.

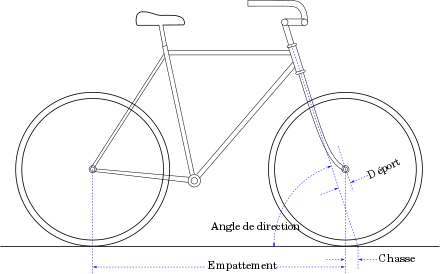
La chasse est un autre facteur qui influence la maniabilité du vélo. Il s'agit de la distance entre le point de contact de la roue avant avec le sol et l'intersection du sol et de l'axe de direction, qui est l'axe autour duquel l'ensemble du mécanisme de direction pivote (fourche, guidon, roue avant). Sur une bicyclette traditionnelle, où l'axe de direction est en retrait de la verticale, la chasse fait tourner la roue avant dans la direction dans laquelle le vélo penche, indépendamment de sa vitesse[5]. Ce phénomène est aisément observable en poussant un vélo à l'arrêt d'un côté donné. La roue avant devrait tourner également dans cette direction, du fait de la gravité.

Plus un vélo a de chasse, plus il est stable. Les vélos à chasse négative (où le point de contact est en avant de l'intersection de l'axe de direction avec le sol) peuvent être conduits, mais sont extrêmement instables. Inversement, les vélos qui accusent une chasse trop importante virent plus difficilement. En général, les vélos de course ont plus de chasse que les vélos de tourisme ou les VTT. Dans le cas des VTT, une chasse moins importante permet d'accroître la précision de la trajectoire, et de préserver l'équilibre du cycliste lorsque sa roue avant heurte des obstacles. Les vélos de tourisme sont construits avec une chasse faible afin de permettre au cycliste de contrôler son vélo lorsqu'il est particulièrement chargé et possède un centre de gravité plus bas. En conséquence, un vélo de tourisme peut paraître instable lorsqu'il n'est pas chargé. Sur les vélos, le cintre de la fourche, qui prend la forme d'une courbe à l'avant de l'axe de direction en bas de la fourche, est utilisée pour diminuer la chasse[10]. Dans le cas des motos et sur certains VTT, la fourche avant n'est pas cintrée mais droite. La diminution de la chasse s'obtient par décalage de l'axe du moyeu par rapport à l'axe de la fourche, soit au niveau de la fixation du moyeu, soit au niveau de la pièce d'articulation de la fourche[11].

La chasse est une fonction de l'angle avant, du cintre et de la taille de la roue qui s'exprime[12]:

${\displaystyle {\text{Chasse}}={\frac {(R\cos(A)-C)}{\sin(A)}}}$

où ${\displaystyle R}$ est le rayon de la roue, ${\displaystyle A}$ l'angle avant mesuré dans le sens des aiguilles d'une montre, et ${\displaystyle C}$ le cintre. La chasse peut être accrue en accroissant la taille de la roue, en réduisant l'angle avant, ou en réduisant le cintre de la fourche.

Une étude empirique de Whitt et Wilson[5] a révélé que :

• les vélos de tourisme ont un angle avant compris entre 72° et 73° et une chasse de 43,0 à 60,0 mm ;
• les vélos de course ont un angle avant compris entre 73° et 74° et une chasse de 28,0 à 45,0 mm ;
• les vélos de piste ont un angle avant de 75° et une chasse de 23,5 à 37,0 mm.

Un autre facteur susceptible de contribuer à l'équilibre d'un vélo traditionnel est la répartition de la masse dans le mécanisme de direction, qui est composé de la roue avant, de la fourche et du guidon. Si le centre de gravité du mécanisme de direction se trouve à l'avant de l'axe de direction, la force de gravité fait tourner la roue dans la direction dans laquelle le vélo penche. Ce phénomène peut être observé en penchant un vélo à l'arrêt. La roue avant tourne généralement aussi dans cette direction indépendamment de toute interaction avec le sol[13] D'autres paramètres, comme la position d'avant en arrière du centre de gravité ou sa hauteur contribuent aussi au comportement dynamique du vélo[5]^,[13].

Effet gyroscopique sur la roue avant d'un vélo. L'application d'un couple à l'axe d'inclinaison (en vert) provoque un couple de réaction appliqué à l'axe de direction (en bleu).

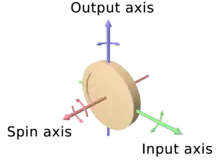
Dans la plupart des vélos, le rôle de l'effet gyroscopique est d'aider à tourner la roue avant dans la direction d'inclinaison. Ce phénomène s'appelle la précession, son ampleur est inversement proportionnelle à la vitesse de rotation de l'objet. Moins la roue avant tourne vite, plus la précession est importante et vice-versa[14]. À l'inverse de la roue avant, la roue arrière n'est pas soumise à ce phénomène à cause des frottements des pneus sur le sol : elle bascule donc de la même manière que si elle était à l'arrêt. Ainsi, l'effet gyroscopique n'empêche pas le basculement.

À faible vitesse, la précession de la roue avant est très forte, ce qui a pour effet de rendre la bicyclette incontrôlable avec une tendance à tourner trop fort (un genre de sur-virage), à se pencher de l'autre côté, ce qui peut entrainer des oscillations et donc une chute. À haute vitesse, à l'inverse la précession est faible, cela rend la bicyclette difficilement manœuvrable : elle a tendance à « refuser » le virage[15]. Le temps caractéristique de cette instabilité est long, de l'ordre de quelques secondes, ce qui la rend facile à contrer. Ainsi, une bicyclette qui va vite peut sembler stable même s'il elle ne l'est pas en réalité et devient instable si elle n'est pas contrôlée.

Une autre contribution des effets gyroscopiques est la création d'un moment (de roulis) par la roue avant lors d'un contre braquage. Cela permet au pilote de lancer un virage rapidement. Par exemple pour un virage à gauche, le pilote d'abord vire à droite, ce qui a pour effet de faire pencher la machine à gauche et d'aider le pilote à engager son virage.

Entre les deux modes d'instabilité mentionnés plus haut et influencés par tous les paramètres cités (empattement, répartition des masses, effet gyroscopique…), il peut y avoir une plage de vitesses où ces effets équilibrent un vélo[16]. Cependant, même sans auto-stabilité, une bicyclette peut être conduite en la maintenant dans l'axe de ses roues[2]. Il est à noter que les effets mentionnés ci-dessus (qui combinés assurent l'auto-stabilité) peuvent être surpassés par des facteurs additionnels comme les frottements dans le jeu de direction ou la raideur des câbles de commandes[5]. Cette vidéo[17] montre une bicyclette auto-stable sans pilote.

Il y a trois principaux modes d'instabilité pour un cycle : il peut se renverser, vaciller ou osciller[18]. Un mode moins connu est le guidonnage arrière, qui est généralement stable[19].

On dit qu'un cycle se renverse quand il chute sans osciller, c'est la simple chute sur le côté. Durant un renversement, la roue avant est généralement orientée dans le sens de la chute, mais pas suffisamment pour compenser la prise d'angle qui augmente jusqu'à une certaine valeur au-delà de laquelle la roue peut se diriger vers le côté opposé. Le renversement peut se produire très doucement à vitesse élevée. Du fait de cette lenteur -la durée du phénomène est de l'ordre de la seconde- il est en fait facile pour le pilote de contrôler ce déséquilibre qui est d'ailleurs utilisé pour amorcer la prise d'angle nécessaire à un virage[19].

La plupart des cycles, de par leur géométrie et centrage, sont stables au renversement à vitesse lente et moins stables à mesure que la vitesse augmente jusqu'à ce qu'ils deviennent instables. Cependant dans la plupart des cas l'interaction du pneu avec le sol est suffisante pour empêcher cette instabilité à haute vitesse[15]^,[19].

Le louvoiement d'un cycle désigne une lente oscillation (0–4 Hz) entre la roue arrière qui se penche et la roue avant qui change de direction. Le cycle tout entier est affecté avec des modifications perceptibles dans sa direction, son angle d'inclinaison (roulis) et son angle de direction. La direction est en opposition de phase (180° de décalage) avec la trajectoire et en quadrature (90°) avec l'inclinaison[19]. Ce clip vidéo[20] illustre ce phénomène.

Dans la plupart des cas, suivant la géométrie et la répartition des masses, le louvoiement est instable à faible vitesse et s'atténue avec une vitesse plus élevée. Alors que l'amplitude peut diminuer avec la vitesse, la fréquence augmente.

Motos inclinées dans un virage.

Le guidonnage décrit une oscillation rapide (4–10 Hz) du train avant (roue avant, fourche et guidon) ; le reste du cycle n'est que très peu affecté. Cette instabilité se produit principalement à haute vitesse et est similaire au phénomène qui se produit sur les chariots de supermarché, les trains d'atterrissage des avions ou les roues avant des voitures[15]^,[19]. Même si le guidonnage peut facilement être supprimé en ajustant sa vitesse, sa position ou son maintien de guidon, il se révèle fatal (chute assurée) s'il n'est pas contrôlé[21]. Ce clip vidéo[22] illustre le guidonnage.

Le guidonnage peut se produire pour d'autres raisons comme une asymétrie de la fourche[23], qui la déséquilibre d'un côté. La réaction s'applique en phase avec ce déséquilibre et la roue tourne du côté opposé. S'il n'y a pas d'amortissement suffisant dans la direction, les oscillations sont entretenues et augmentent jusqu'à la rupture. La fréquence des oscillations peut être modifiée en changeant la vitesse, le poids du cycle ou en augmentant la dureté de la direction, dont le pilote est un élément principal[5].

Une étude a montré que les ondulations de la route peuvent exciter les oscillations dans les virages si leur fréquence est en adéquation avec la vitesse du véhicule et les paramètres masse cycle et dureté de la direction. Ce phénomène peut être évité avec un amortisseur de direction performant, et diminué en accroissant la pression dans les pneus[24].

Vélos inclinés dans un virage.

Le terme de guidonnage arrière est utilisé pour décrire les oscillations durant lesquelles l'angle de roulis et de lacet sont presque en phase, et tous deux en opposition de phase avec l'angle de direction. La fréquence de ces oscillations est modérée avec un maximum d'environ 6,5 Hz. Le guidonnage arrière est un phénomène très amorti et disparait rapidement quand la vitesse augmente.

On peut caractériser les effets de la géométrie du cycle sur l'instabilité en examinant les valeurs propres des équations du mouvement dans leur version linéarisée[25]. Pour plus de détails sur les équations du mouvement et les valeurs propres, se reporter à la section théorique. Des conclusions générales sont décrites ici.

La rigidité en torsion et en flexion du train arrière et de l'axe de la roue modifient l'amortissement du guidonnage de manière substantielle. Un grand empattement, une chasse importante et un angle de chasse faible augmente l'amortissement du guidonnage. La distorsion latérale peut être contrée en plaçant l'axe de rotation de la fourche plus bas.

La tendance au vacillement en courbe est amplifiée par un mauvais amortissement dans la suspension arrière. Les caractéristiques viscoélastiques du pneu arrière déterminant sa réponse aux efforts dynamiques de réaction au sol contribuent fortement à l'amortissement du vacillement. La caractéristiques du pneu avant influent en revanche moins. Une concentration de masse à l'arrière favorise la tendance au vacillement. En revanche, un centrage plus arrière associé à une rigidité et un amortissement adaptés sont efficaces dans la surpression du guidonnage et du vacillement.

De ce fait, autant pour le guidonnage que pour le vacillement, la pression des pneumatiques est un paramètre primordial pour la stabilité des cycles à haute vitesse.

Cependant, à la différence des véhicules d'autres points d'appui, les deux-roues doivent pencher dans un virage pour compenser les forces qu'ils subissent, en particulier la force centrifuge. L'angle d'inclinaison ${\displaystyle \theta }$ peut se calculer en utilisant les équations du mouvement circulaire, où ${\displaystyle v}$ est la vitesse de déplacement, ${\displaystyle r}$ le rayon de virage et ${\displaystyle g}$ la valeur du champ de pesanteur[14].

Par exemple, un cycle à l'équilibre qui opère un virage de rayon 10 m à la vitesse de 10 m/s — soit 36 km/h — doit avoir un angle de chasse de 45°. Le pilote peut se pencher par rapport au cycle de façon à garder soit son torse soit le vélo plus ou moins à la verticale. L'angle de chasse est l'angle entre le plan horizontal d'une part et le plan formé par les deux points de contact des pneus avec le sol et le centre de gravité de l'ensemble pilote-machine.

Cette inclinaison diminue le rayon de courbe réel proportionnellement au cosinus de l'angle. L'angle d'inclinaison équivalent peut être approché (à 2 % de la valeur exacte) par :

${\displaystyle r={\frac {e\cos \left(\theta \right)}{\delta \cos \left(\phi \right)}}}$

où ${\displaystyle r}$ est le rayon approché, ${\displaystyle e}$ est l'empattement, ${\displaystyle \theta }$ est l'angle d'inclinaison, ${\displaystyle \delta }$ est l'angle de direction et ${\displaystyle \phi }$ est l'angle de chasse[19].

Lorsque le cycle se penche, les zones de contacts des pneus avec le sol se déplacent vers l'extérieur du virage ce qui entraine une usure. Dans le monde de la moto, les portions du pneu qui demeurent intactes sont parfois appelées les « chickens strips » (bandes de peur).

Afin de déclencher une courbe et la prise d'angle nécessaire, un cycle doit momentanément être dirigé dans la direction opposée. Cette techniques est souvent appelée contre braquage. Ce mouvement rapide déplace les roues de la verticale du centre de gravité et provoque ainsi la prise d'angle. Quand il n'y a pas d'actions extérieures comme un vent latéral dans le bon timing qui provoque l'inclinaison, le contre braquage est utilisé à chaque virage[14].

Quand l'inclinaison approche de l'angle voulu, la roue avant doit être dirigée vers l'intérieur de la courbe et en fonction de la vitesse, du rayon de courbe et du besoin de maintenir l'angle. Une fois la courbe engagée, le rayon ne peut être changé que par un changement approprié de l'angle d'inclinaison. Cela ne peut être fait qu'en contre braquant momentanément encore plus de manière à augmenter l'inclinaison et donc le rayon de courbe. Pour sortir de la courbe, il faut également contre braquer mais cette fois-ci de manière à diminuer le rayon de courbe et donc augmenter les effets inertiels et ainsi diminuer l'inclinaison [26].

Une fois la courbe engagée, le couple qui doit être appliqué au mécanisme de direction pour maintenir un rayon de courbe constant dépend de la vitesse de déplacement, de la géométrie et de la répartition des masses du cycle[15]. Avec une vitesse inférieur à la vitesse limite de renversement, définie ci-dessous dans la section « Valeurs propres », aussi appelée vitesse « d'inversion », le caractère auto-stable du cycle le fait tourner vers l'intérieur de la courbe, ce qui l'équilibre et le fait sortir de la courbe, à moins qu'un couple ne soit appliqué dans la direction opposée au virage. Avec une vitesse supérieure à la vitesse de renversement, l'instabilité a tendance à faire tourner la direction vers l'extérieur du virage, ce qui augmente l'inclinaison, à moins qu'un couple ne soit appliqué vers l'intérieur du virage. À la vitesse de renversement, aucun couple extérieur appliqué à la direction n'est nécessaire pour maintenir l'équilibre en courbe.

Alors que le contre-braquage est généralement initié en appliquant un couple directement au guidon, sur les véhicules légers, comme les bicyclettes, cela peut se faire en déplaçant le poids du pilote. Si le pilote se penche vers la droite, le vélo se penchera dans l'autre sens, afin de respecter la conservation du moment angulaire, et que le centre de gravité équivalent du système (pilote+cycle) reste dans le même plan vertical. Ce mouvement du cycle vers la gauche provoque un braquage vers la gauche et déclenche un virage vers la droite de la même manière que si le pilote avait effectué un contre braquage vers la gauche en tournant son guidon[14]. Il est à noter que cette technique peut être compliquée par les frottements internes à la direction et la raideur des câbles de commandes.

Tourner la roue avant provoque un moment de roulis causé par la précession gyroscopique. La valeur de ce moment est proportionnelle au moment d'inertie de la roue avant, sa vitesse de rotation(dans le sens d'avance), la vitesse à laquelle le pilote tourne le guidon et le cosinus de l'angle entre l'axe de direction et la verticale[19].

Pour une moto roulant à 22 m/s, dont la roue avant possède un moment d'inertie de t 0,6 kgm², tourner la roue avant d'un degré en une demi-seconde génère un moment de roulis de 3,5 N m. En comparaison, la force latérale sur le pneu avant lorsqu'il « sort » du plan vertical de la moto atteint un maximum de 50 N. Ceci, agissant à 0,6 m (2 ft) du centre de masse, génère un moment de roulis de 30 N m.

Même si le moment issu des effets gyroscopiques atteint seulement 12 % de cette valeur, il peut jouer un rôle significatif car il agit dès que le pilote applique l'effort, et non pas progressivement lorsque les roues se décalent, cela peut être très utile en compétition motocycliste.

Du fait des bénéfices théoriques, comme par exemple un rayon de braquage très faible à faible vitesse, certains ont essayé de concevoir des motocyclettes où les deux roues sont directrices. Un prototype fonctionnel conçu par Ian Drysdale en Australie a été rapporté comme « fonctionnant très bien »[27]^,[28].

Une des questions de conception est de savoir s'il faut assurer un contrôle actif de la roue arrière ou au contraire la laisser libre de dévier. Dans le cas du contrôle actif, l'algorithme de contrôle doit décider s'il doit diriger la roue arrière dans le même sens que la roue avant ou pas, à quel moment et avec quelle intensité. On peut trouver un exemple d'implémentation des 2 roues directrices sur les bicyclettes Sideway laisse le pilote diriger les deux roues directement.

En raison de ses bénéfices sur le papier, plusieurs tentatives ont été faites pour construire un cycle avec la roue arrière directrice. La société Bendix a essayé de construire un tel cycle et le département américain des transports a commandé la construction d'une moto à roue arrière directrice : les deux prototypes ne sont pas pilotables. Rainbow Trainers Inc. offre 5 000 US$ à la première personne capable de piloter un cycle à roue arrière directrice[29]. Un exemple documenté de réussite dans le pilotage d'un tel cycle est celui de L. H. Laiterman du MIT sur un cycle allongé spécifique. La difficulté réside dans le fait que tourner la roue arrière vers la droite déclenche un déplacement du centre de gravité vers la droite et vice versa. Cela complique la tâche de compensation des inclinaisons provoquées par l'extérieur[30]. L'étude des valeurs propres montre que le cycle à roue arrière directrice est intrinsèquement instable.

Entre les deux extrêmes : les cycles classiques à roue avant directrice et ceux à roue arrière directrice, il existe les cycles où le point de pivot de la direction est situé entre les deux points extrêmes, on les appelle les cycles à direction centrale. Cette solution autorise des systèmes à traction avant simple et se trouve être assez stable, comme le montrent de nombreuses images[31]^,[32]. Ces solutions ont généralement des angles de chasse très larges (entre 40° et 65°) et une chasse positive ou négative. Le constructeur d'un cycle à chasse négative déclare que diriger un cycle hors de la trajectoire rectiligne force le pilote à se relever légèrement ce qui compense l'effet déstabilisant de la chasse négative [33].

L'effet de barre -'Tiller effect'- est l'expression utilisée pour décrire la manière dont un guidon qui s'étend fortement en arrière de l'axe de direction se déplace latéralement comme la barre d'un bateau. En effet il faut déplacer le guidon vers la droite pour virer à gauche et vice versa. Cette situation se retrouve souvent sur les cycles de type cruiser, certains modèles couchés et même certaines motos cruiser. Cela peut être troublant voire gênant quand cela limite la possibilité de tourner à cause de l'incompatibilité avec l'amplitude des bras[34]. Le conducteur ayant naturellement tendance à maintenir le guidon centré, cela améliore la stabilité induite par le pilote.

Les pneumatiques ont une forte influence sur la maniabilité du cycle, en particulier sur les motos[35]^,[19]. Les pneus ont, dans la réalité, une surface de contact finie avec le sol fini et peuvent donc générer un couple de frottement. Ainsi, pendant un virage, ils peuvent déraper sur le côté et ainsi provoquer un couple par rapport à l'axe normal au plan de contact.

Un tel couple est généré par l'asymétrie du dérapage le long de la surface de contact.