Entrelacs brunnien

En mathématiques, plus précisément en théorie des nœuds, une sous-branche de la topologie, un entrelacs brunnien est un entrelacs non trivial (en) qui devient trivial si l'un quelconque de ses composants est enlevé. En d'autres termes, couper n'importe laquelle des boucles libère toutes les boucles de l'entrelacs. L'adjectif brunnien vient de Hermann Brunn, qui a rédigé l'article Über Verkettung en 1892 dans lequel il prend pour exemples de tels nœuds.

Ce nœud à quatre brins est un entrelacs brunnien.
Entrelacs brunnien à six composants.

Exemples

L'entrelacs brunnien le plus simple et le plus connu est le nœud borroméen, un entrelacs de trois éléments non noués entre eux. À partir de trois éléments, il existe une infinité d'entrelacements possibles contenant le même nombre de boucles. Voici quelques exemples d'entrelacs brunniens à trois composants.

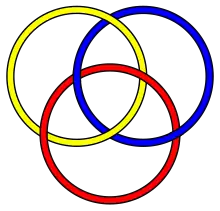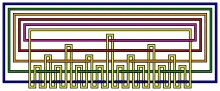
  • Un nœud borroméen est un nœud brunnien.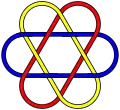
  • Entrelacs brunnien à 12 croisements
  • Entrelacs brunnien à 18 croisements
  • Entrelacs brunnien à 24 croisements

Classification


(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Brunnian link » (voir la liste des auteurs).
  • Portail des mathématiques
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.