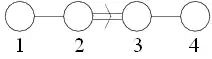
F4 (mathématiques)

En mathématiques, F₄ est un groupe de Lie exceptionnel de type complexe. Son algèbre de Lie est notée ${\mathfrak {f}}_{4}$ . F₄ est de rang 4 et de dimension 52. Sa forme compacte est simplement connexe et son groupe d'automorphismes est le groupe trivial. Sa représentation fondamentale est de dimension 26.

Pour les articles homonymes, voir F4.

La forme compacte réelle de F₄ est le groupe d'isométries d'une variété riemannienne de dimension 16, connu également sous le nom de plan projectif octonionique, OP², ou plan de Cayley (en). Ceci peut être vu en utilisant la construction du carré magique (en), étudiée en détail par Hans Freudenthal et Jacques Tits.

Il existe trois formes réelles de ce groupe, une compacte, une déployée, et une troisième.

Algèbre

Diagramme de Dynkin

Racines de F₄

(\pm 1,\pm 1,0,0)

(\pm 1,0,\pm 1,0)

(\pm 1,0,0,\pm 1)

(0,\pm 1,\pm 1,0)

(0,\pm 1,0,\pm 1)

(0,0,\pm 1,\pm 1)

(\pm 1,0,0,0)

(0,\pm 1,0,0)

(0,0,\pm 1,0)

(0,0,0,\pm 1)

\left(\pm {\frac {1}{2}},\pm {\frac {1}{2}},\pm {\frac {1}{2}},\pm {\frac {1}{2}}\right)

Racines simples :

(0,0,0,1)

(0,0,1,-1)

(0,1,-1,0)

\left({\frac {1}{2}},-{\frac {1}{2}},-{\frac {1}{2}},-{\frac {1}{2}}\right)

Matrice de Cartan

{\begin{pmatrix}2&-1&0&0\\-1&2&-2&0\\0&-1&2&-1\\0&0&-1&2\end{pmatrix}}

Lien externe

(en) F₄ sur le site The Octonions de John C. Baez, à l'UCLA

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « F4 (mathematics) » (voir la liste des auteurs).

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.