Fenêtre de Viviani
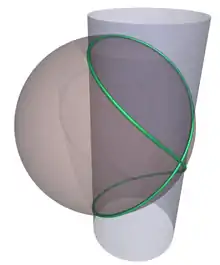
La fenêtre de Viviani est une courbe algébrique gauche, et une courbe fermée, définie comme l'intersection d'une sphère et d'un cylindre circulaire de rayon moitié de celui de la sphère, et passant par le centre de la sphère.
Pour les articles homonymes, voir Fenêtre (homonymie).
Vincenzo Viviani proposa en 1692 le problème d'architecture suivant[1] : il s'agissait de percer une coupole hémisphérique de quatre fenêtres de telle façon que la surface restante de la coupole soit quarrable. John Wallis, Gottfried Wilhelm Leibniz et Jean Bernoulli étudièrent naturellement le cas simple de fenêtres circulaires, et durent étudier la courbe intersection du cylindre et de l'hémisphère, donnant à cette courbe le nom de « fenêtre de Viviani »[2].
L'architecte Paul Andreu a dessiné le dôme du Musée maritime d'Ōsaka, en disposant les armatures selon un réseau de courbes de Viviani parallèles.
Équations de la fenêtre de Viviani
On a les représentations suivantes[3] (pour une sphère de rayon R) :
- Système d’équations cartésiennes : et , cette dernière expression venant de celle d'un cylindre de centre , de rayon et d'axe parallèle à l'axe des : .
- Paramétrisation cartésienne :
La sphère peut être paramétrée par où
En reportant dans l'équation du cylindre, on obtient :
Donc et le paramétrage de la courbe de Viviani :
avec
Intersection d'une sphère et d'un cône
En soustrayant l'équation de la sphère et deux fois l'équation du cylindre, on obtient l'équation l'équation d'un cône :
La courbe de Viviani est ainsi également l'intersection de la sphère et de ce cône[3].
Notes et références

- L'énoncé complet du problème est donné dans l'article de D. Lanier, cf. infra.
- Cf. Chasles, p. 141.
- Robert Ferréol, « Courbe de Viviani », sur Encyclopédie des formes mathématiques remarquables
Bibliographie
- Michel Chasles, Aperçu historique sur l'origine et le développement des méthodes en géométrie (1837), impr. Hayez, Bruxelles
- Michel Serres, Le système de Leibnitz et ses modèles mathématiques (1968, rééd. 2007) éd. PUF, coll. Épiméthée (ISBN 2130433898)
- (fr) Denis Lanier, « Leibniz, la nouvelle analyse et la géométrie ou enquête sur la fenêtre de Viviani », sur NUMDAM, Cahiers du séminaire d'histoire des mathématiques, vol. 8, (consulté le ), p. 203-227
- Portail de la géométrie