Repère de Frenet
En cinématique ou en géométrie différentielle, le repère de Frenet ou repère de Serret-Frenet est un outil d'étude du comportement local des courbes. Il s'agit d'un repère local associé à un point P, décrivant une courbe (C). Son mode de construction est différent selon que l'espace ambiant est de dimension 2 (courbe plane) ou 3 (courbe gauche) ; il est possible également de définir un repère de Frenet en toute dimension, pourvu que la courbe vérifie des conditions différentielles simples.
Pour les articles homonymes, voir Repère.
Le repère de Frenet, et les formules de Frenet donnant les dérivées des vecteurs de ce repère, permettent de mener de façon systématique des calculs de courbure, de torsion pour les courbes gauches et d'introduire des concepts géométriques associés aux courbes : cercle osculateur, plan osculateur, parallélisme des courbes (en)…
Arc paramétré plan
Le cadre est le plan euclidien orienté rapporté à un repère orthonormal, les coordonnées sont notées et et l'origine . L'arc est supposé défini par des fonctions de classe , et régulier[1],[2]. Pour simplifier l'étude, on utilise un paramétrage normal , où est l’abscisse curviligne.
On se place en un point particulier de paramètre . Comme l'arc est paramétré par l'abscisse curviligne, le vecteur dérivé, , est unitaire et tangent à la courbe, il est dirigé dans le sens du mouvement. Il porte le nom de vecteur tangent unitaire à la courbe et est noté traditionnellement .
Le vecteur normal unitaire complète en une base orthonormale directe, appelée base de Frenet. Il s'obtient en effectuant une rotation de (quart de tour dans le sens direct) du vecteur [1],[2]. Le repère de Frenet est constitué en prenant en outre pour origine le point . Très souvent on abrège les notations en omettant le paramètre .
Le repère de Frenet est un repère mobile (en) puisque les éléments de ce repère changent selon le point considéré. En physique, il ne faut pas confondre cette notion avec celle de référentiel : puisque les vecteurs de Frenet se déplacent avec le point, s'il s'agissait d'un référentiel alors le vecteur position serait le vecteur nul, et la vitesse serait également nulle.
Remarque : il arrive qu'on introduise le vecteur par , en plongeant le plan euclidien dans un espace de dimension trois, et en notant un vecteur complétant la base du plan en une base orthonormale directe[3],[4]. Les deux façons de procéder sont équivalentes.
La courbure et les formules de Frenet

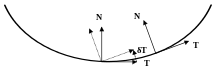
Si on suppose de plus que l'arc régulier de classe est de classe , on peut définir la courbure algébrique[5]. Comme les vecteurs de la base de Frenet forment en permanence une base orthonormale, leurs dérivées vérifient un certain nombre de relations. Notamment le vecteur dérivé de est orthogonal à ; il existe donc pour le point de paramètre un coefficient tel que
On donne à le nom de courbure (algébrique) de la courbe, elle est homogène à l'inverse d'une longueur. Pour une courbe bi-régulière, son inverse est souvent utilisé en cinématique et porte le nom de rayon de courbure algébrique .
On peut également interpréter la courbure comme la vitesse de rotation de la base de Frenet par rapport à une direction fixe (encore une fois, en paramétrage normal) : voir à ce sujet l'article courbure d'un arc.
On appelle centre de courbure de la courbe au point le point de coordonnées dans le repère de Frenet. Vectoriellement, il est obtenu de la façon suivante :
Le cercle de centre et de rayon est appelé cercle de courbure ou cercle osculateur à la courbe en . Il approche en général la courbe mieux que ne le fait la tangente. Courbure et cercle de courbure donnent non seulement une idée de la direction dans laquelle la courbe avance (direction de la tangente), mais aussi de sa tendance à tourner de part et d'autre de cette tangente.
Les formules de Frenet, donnant les dérivées des vecteurs de la base de Frenet, s'écrivent à l'aide de la courbure[6]
Cas d'un paramétrage euclidien quelconque
Reprenant un arc paramétré birégulier, sans le supposer donné en paramétrage normal, il suffit pour exploiter les formules de Frenet de faire le lien entre la dérivation par rapport à ou à , ce qui se fait au moyen de la vitesse scalaire
Il est alors possible d'expliciter les vecteurs vitesse et accélération dans la base de Frenet[7]
On retrouve que le vecteur vitesse est tangentiel, allant dans le sens du mouvement. La première composante du vecteur accélération dans la base de Frenet est appelée accélération tangentielle ; elle rend compte de la variation de la vitesse scalaire. L'autre composante, appelée accélération normale , est influencée par la géométrie de la courbe : est d'autant plus forte que le virage effectué est plus serré, et aussi que la vitesse est plus élevée.
Il est donc possible d'évaluer le rayon de courbure algébrique en formant le déterminant de ces deux vecteurs[7]
On retrouve la proposition VI des Principia de Newton.
On vérifie l'homogénéité des dimensions :
Propriétés d'invariance
Il est important de réaliser que le repère de Frenet a été défini à partir d'un paramétrage normal de la courbe. Tous les reparamétrages préservant l'orientation donneront la même base de Frenet, et la même valeur de la courbure. Il y a également invariance par changement du repère fixe de référence.
En revanche les changements d'orientation de la courbe ou de l'espace ambiant renversent certains signes. Précisément
- si on renverse l'orientation de la courbe, l'abscisse curviligne est changée en son opposé, le vecteur , le vecteur également[2].. La courbure algébrique est elle aussi renversée[5], de sorte que le cercle osculateur reste, lui, inchangé.
- si on renverse l'orientation de l'espace ambiant, l'abscisse curviligne et le vecteur sont inchangés, mais le vecteur est changé en son opposé[2], ainsi que la courbure[5].
Exemples
Considérons un mouvement circulaire accéléré
En dérivant on obtient les coordonnées du vecteur vitesse :
Elle s'écrit sous la forme avec
Le vecteur normal unitaire est donc
En confrontant les deux égalités
- et
on trouve que la courbure γ vaut 1. Le rayon de courbure est constant, égal à 1. Le cercle osculateur coïncide en permanence avec le cercle sur lequel la trajectoire est inscrite. On aurait pu éviter tous ces calculs en utilisant le reparamétrage u=t2.
Si la courbe est donnée en coordonnées polaires paramétriques r(t),θ(t), les vecteurs vitesse et accélération peuvent être calculés dans la base mobile. On note par un point la dérivation par rapport au paramètre t
La courbure (inverse à une longueur) est donnée par
et le rayon de courbure (L) par :
Courbe gauche
Introduction du repère de Frenet
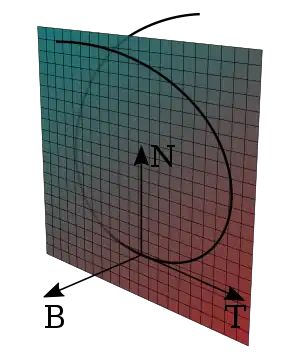
On considère cette fois une courbe de l'espace euclidien orienté à trois dimensions, de classe régulière, orientée et simple[8] paramétrée par l'abscisse curviligne f(s)=(x(s),y(s),z(s)). Le repère de Frenet au point de paramètre s, souvent appelé aussi trièdre de Frenet est défini par trois vecteurs unitaires T, N, B formant une base orthonormale directe, et en prenant encore comme origine le point de paramètre s.
Le vecteur T, vecteur tangent unitaire, est introduit comme dans le plan.
On suppose de nouveau l'arc birégulier. Alors le vecteur est orthogonal au vecteur tangent unitaire, et non nul. On définit cette fois le vecteur normal unitaire et la courbure simultanément en posant[9],[10]
On complète enfin en une base orthonormale directe en prenant pour troisième vecteur de base, appelé vecteur binormal
Cette fois la description géométrique est la suivante : le vecteur T dirige la tangente à la courbe. Le couple (T,N) engendre un plan appelé plan osculateur à la courbe. Ce plan contient la tangente et le cercle osculateur à la courbe. Par la convention de positivité de la courbure, le vecteur N est cette fois dirigé vers le centre de courbure. Les formules donnant vitesse et accélération dans la base de Frenet sont identiques à celles obtenues pour une courbe plane.
Le trièdre de Frenet permet de définir deux autres plans :
- Le plan rectifiant engendré par le couple (T,B) et normal au rayon de courbure;
- Le plan normal, engendré par le couple (N,B) et normal à la tangente.
Formules de Frenet
On suppose désormais la courbe de classe et birégulière[9],[10]. Le vecteur normal unitaire, le vecteur binormal sont par construction des fonctions dérivables de s. En outre, comme T, N, B constituent une base orthonormale pour toute valeur de s, les vecteurs dérivés vérifient un certain nombre de relations. Finalement, il existe un coefficient appelé torsion au point de paramètre s tel que les relations suivantes soient vérifiées[11]:
Remarque: on trouve parfois la torsion définie avec le signe opposé[9], il suffira alors d'inverser les signes devant τ dans les formules ci-dessus et ci-dessous. En ajoutant la formule de dérivation de T indiquée au-dessus, on obtient un ensemble de trois formules appelées formules de Frenet pour les courbes gauches. On peut les résumer symboliquement en utilisant une matrice
L'orthonormalité des vecteurs de la base de Frenet se traduit par l'antisymétrie de la matrice : il s'agit en fait ici d'un résultat général sur les bases mobiles (en).
La torsion
Le facteur τ a néanmoins une interprétation géométrique : il s'agit de la tendance à s'écarter du plan osculateur (de même que la courbure mesure la tendance à s'écarter de la tangente). La torsion est donc ce qui fait que la courbe est non plane. Il convient de voir dans ces « corrections successives » du comportement de la courbe, courbure et torsion, les termes successifs d'un développement limité au point de paramètre s.
On peut donner l'expression de la courbure et de la torsion, pour un paramétrage f(t) quelconque[12],[13]:
où le crochet désigne le produit mixte.
Applications
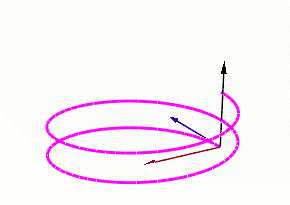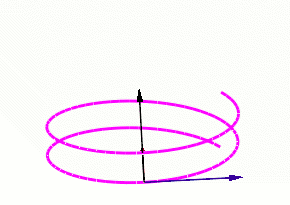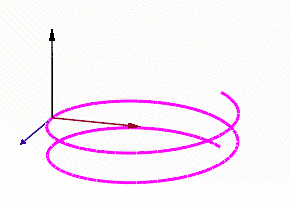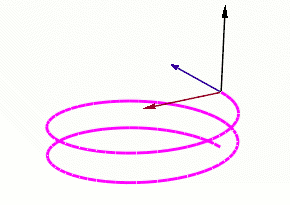
En cinématique du point, la courbe considérée est la trajectoire parcourue par le point. le vecteur vitesse est toujours colinéaire au vecteur tangent.
On peut par ailleurs décomposer le vecteur accélération en une composante normale et une composante tangentielle, en le projetant sur le repère de Frenet. La composante normale décrit le changement de direction de la trajectoire (courbure), et le vecteur tangentiel décrit la variation de la norme du vecteur vitesse.
Généralisation en dimension quelconque
Une définition analogue est possible dans , ou plus généralement dans un espace euclidien quelconque :
Notes et références
- Gérard Debeaumarché, Francis Dorra, Max Hochart, Mathématiques PSI-PSI*: Cours complet avec tests, exercices et problèmes corrigés, Pearson Education France, 2010, p.292 Aperçu en ligne
- Jacqueline Lelong-Ferrand et Jean-Marie Arnaudiès, Cours de Mathématiques : Géométrie et Cinématique, t. 3, Paris, Bordas, , p 326
- Nicholas M. Patrikalakis, Takashi Maekawa et Wonjoon Cho, « Shape Interrogation for Computer Aided Design and Manufacturing (Hyperbook Edition) - Differential Geometry - 2.2 Principal normal and curvature », Massachusetts Institute of Technology, , formule 2.24
- Tauvel 2005, p. 358.
- Lelong-Ferrand et Arnaudiès 1977, p. 327.
- Lelong-Ferrand et Arnaudiès 1977, p. 328.
- Lelong-Ferrand et Arnaudiès 1977, p. 329.
- Patrice Tauvel, Géométrie : Agrégation - Licence 3e année - Master, Paris, Dunod, , p 353
- Tauvel 2005, p. 355.
- Lelong-Ferrand et Arnaudiès 1977, p. 347.
- Lelong-Ferrand et Arnaudiès 1977, p. 349.
- Tauvel 2005, p. 356.
- Lelong-Ferrand et Arnaudiès 1977, p. 351-52.
Voir aussi
- Portail de la géométrie
- Portail de la physique