Cercle osculateur

Une courbe suffisamment régulière possède un cercle de courbure en tout point birégulier, c'est-à-dire en tout point pour lesquels les vecteurs vitesse et accélération sont non colinéaires.

Il est possible de définir le cercle de courbure à partir de la courbure et des éléments du repère de Frenet, ou au contraire de donner une définition géométrique du cercle de courbure, et de définir à partir de lui la courbure.

Défini de façon directe, le cercle de courbure est le cercle le plus proche de la courbe en M, c'est l'unique cercle "osculateur" à la courbe en ce point, c'est-à-dire ayant un contact avec elle d'ordre au moins deux. Ceci signifie qu'il constitue une très bonne approximation de la courbe, meilleure qu'un cercle tangent quelconque. En effet, il donne non seulement une idée de la direction dans laquelle la courbe avance (direction de la tangente), mais aussi de sa tendance à tourner de part ou d'autre de la tangente.

Le cercle de courbure au point de paramètre t₀ est aussi la limite, lorsque t et t' tendent vers t₀, du cercle passant par les points de paramètre t , t', et t₀, ou encore la limite, lorsque t tend vers t₀, du cercle passant par les points de paramètre t et t₀ et tangent à la courbe en t₀ (voir les animations ci-dessous).

Le rayon du cercle de courbure en un point M de la courbe est appelé rayon de courbure, et son inverse la courbure en ce point. Le cercle de courbure est centré sur la droite normale à la courbe en P, et situé à l'intérieur de la concavité de la courbe (la courbe s'enroule autour de son centre de courbure). La tangente à la courbe en P est donc tangente également au cercle de courbure.

• 
  Évolution du cercle passant par un point fixé de la courbe et deux autres points. Lorsque ces deux points tendent vers le premier, le cercle tend vers le cercle osculateur.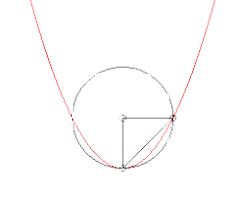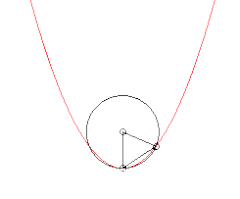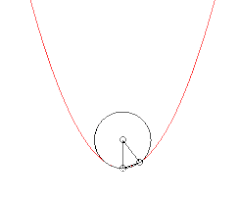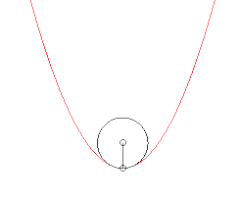
• 
  Évolution du cercle tangent en un point de la courbe et passant par un autre point, lorsque ce point tend vers le premier.
• 
  Évolution du cercle osculateur en un point, lorsque ce point parcourt la courbe. Le cercle traverse la courbe, sauf lorsqu'il est aux sommets ; au point d'inflexion, il dégénère en une droite (courbure nulle) ;

Le centre de courbure peut donc être exprimé à partir des éléments du repère de Frénet par la formule suivante

${\displaystyle {\overrightarrow {P\Omega }}={\frac {1}{\gamma }}{\vec {N}}}$

Le centre de courbure en P peut être vu également comme le point d'intersection de la normale en P avec une normale infiniment proche. De ce point de vue, la courbe formée par les centres de courbure successifs, appelée développée de la courbe initiale, est l'enveloppe de la famille des normales à la courbe.

Toutes les propriétés précédentes peuvent être établies de façon analytique. Pour simplifier au maximum l'étude, on munit l'arc d'un paramétrage par l'abscisse curviligne en prenant pour origine le point en lequel on veut calculer le cercle de courbure. Avec ces hypothèses, les vecteurs dérivés successifs sont

${\displaystyle {\frac {dM}{ds}}=T\qquad {\frac {d^{2}M}{ds^{2}}}=\gamma N\qquad {\frac {d^{3}M}{ds^{3}}}={\frac {d\gamma }{ds}}N-\gamma ^{2}T}$

où γ est la courbure.

Les calculs se feront dans le repère de Frenet associé au point d'étude : on note X(s) et Y(s) les coordonnées des points de la courbe relativement à ce repère. Alors

${\displaystyle {\begin{cases}X(0)=0\qquad Y(0)=0\\X'(0)=1\qquad Y'(0)=0\\X''(0)=0\qquad Y''(0)=\gamma (0)\\X'''(0)=-\gamma (0)^{2}\qquad Y'''(0)={\frac {d\gamma }{ds}}(0)\end{cases}}}$

Si un cercle est osculateur à la courbe au point s=0, il admet pour tangente la droite Y=0, donc son centre se trouve en un point de coordonnées du type (0,Y₀). On forme l'équation d'un tel cercle : X²+(Y-Y₀)²=Y₀². On peut donc vérifier si le point courant sur la courbe est à l'intérieur ou à l'extérieur en calculant le développement limité de l'expression

${\displaystyle X(s)^{2}+(Y(s)-Y_{0})^{2}-Y_{0}^{2}=(1-Y_{0}\gamma (0))s^{2}-{\frac {Y_{0}}{3}}{\frac {d\gamma }{ds}}(0)s^{3}+o(s^{3})}$

La condition nécessaire et suffisante pour que le cercle soit osculateur est l'annulation du premier terme, ce qui donne bien ${\displaystyle Y_{0}={\frac {1}{\gamma (0)}}}$ rayon de courbure. Ceci prouve l'existence et l'unicité du cercle osculateur.

Cercle surosculateur avec un contact d'ordre 4

En outre la position par rapport au cercle osculateur est donnée par le signe de l'expression ${\displaystyle -{\frac {Y_{0}}{3}}{\frac {d\gamma }{ds}}(0)s^{3}+o(s^{3})}$:

• si ${\displaystyle {\frac {d\gamma }{ds}}(0)\neq 0}$ (cas le plus fréquent), la courbe traverse le cercle osculateur en ce point. La multiplicité de l'intersection est 3 [3] (attention, cela correspond à un ordre 2 en tant que point de contact).
• sinon le point d'étude est un sommet : l'ordre de multiplicité du point d'intersection est 4 ou plus, le cercle est dit surosculateur. Dans ce dernier cas il faudrait poursuivre le développement limité pour connaître la position de la courbe. En général elle reste toujours du même côté du cercle surosculateur.

Dans le cas d'une courbe dans l'espace euclidien de dimension 3, on définit le plan osculateur au point de paramètre t₀ comme la limite, lorsque t et t' tendent vers t₀, du plan passant par les points de paramètre t , t', et t₀ , et le cercle osculateur comme la limite du cercle par les points de paramètre t , t', et t₀. Le cercle osculateur se trouve donc dans le plan osculateur, lequel est dirigé par les vecteurs tangent et normal. On peut prendre aussi la limite, lorsque t tend vers t₀, du plan passant par les points de paramètre t et t₀ et contenant la tangente à la courbe en t₀, et de même pour le cercle.

Il existe plusieurs sphères contenant ce cercle. On appelle sphère osculatrice[4], ou surosculatrice[5], la sphère qui minimise l'écart avec la courbe au voisinage du point M considéré. La recherche du centre de la sphère peut se conduire comme précédemment, mais les développements limités doivent être conduits jusqu'à l'ordre 3, en décomposant les vecteurs selon le vecteur tangent T, normal N et binormal B. Les calculs conduisent à choisir ce centre en ${\displaystyle M+{\frac {1}{\gamma }}N-{\frac {\gamma '}{\gamma ^{2}\tau }}B}$, où ${\displaystyle \gamma }$ est la courbure au point M, ${\displaystyle \gamma '}$ sa dérivée par rapport à l'abscisse curviligne, ${\displaystyle \tau }$ la torsion de la courbe au point M. Le projeté orthogonal de ce centre sur le plan osculateur n'est autre que le centre de courbure.

• Polynôme osculateur

• Portail de la géométrie