Développée

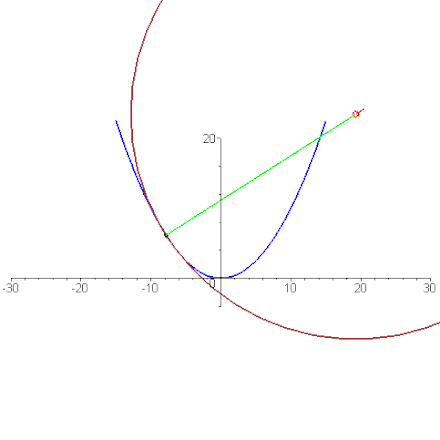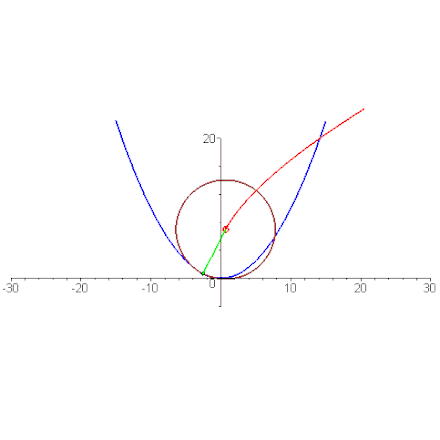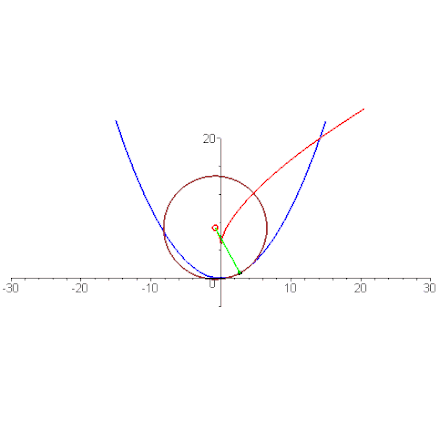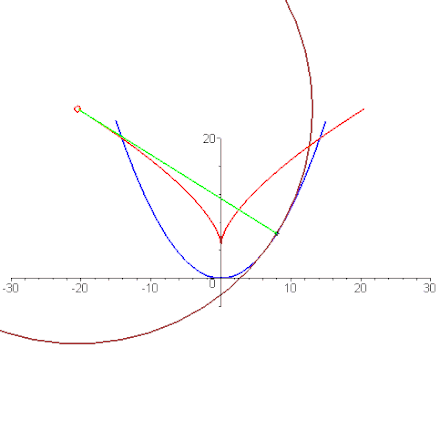
En géométrie, la développée d'une courbe plane est le lieu de ses centres de courbure. On peut aussi la décrire comme l'enveloppe de la famille des droites normales à la courbe.

Développée comme lieu des centre de coubure : La développée (parabole semicubique (en), en rouge vermillon) de la parabole bleue est à la fois l'ensemble des centres des cercles osculateurs (rouge carmin) et l'enveloppe des normales (vertes).

Développée comme enveloppe des normales, ici la développée (en bleu) d'une ellipse (c'est l'image par une dilatation d'une astroïde).

On suppose la courbe suffisamment dérivable et birégulière. Si elle est paramétrée par l'abscisse curviligne sous la forme ${\displaystyle {\vec {f}}(s)}$, le centre de courbure s'obtient en posant

${\displaystyle {\vec {g}}(s)={\overrightarrow {O\Omega (s)}}={\vec {f}}(s)+\gamma (s)^{-1}{\vec {N}}(s)}$

où ${\displaystyle \Omega }$ est le centre de courbure, ${\displaystyle \gamma }$ la courbure et ${\displaystyle {\vec {N}}}$ le vecteur normal au point ${\displaystyle {\vec {f}}(s)}$.

Le vecteur dérivé de la développée est

${\displaystyle {\vec {g'}}(s)={\vec {f'}}(s)+\gamma (s)^{-1}{\vec {N'}}(s)-{\frac {\gamma '(s)}{\gamma (s)^{2}}}{\vec {N}}(s)=-{\frac {\gamma '(s)}{\gamma (s)^{2}}}{\vec {N}}(s)}$

en utilisant les formules de Frenet. On vérifie ainsi que :

• les points stationnaires de la développée g correspondent aux points où la dérivée de la courbure de f s'annule, en particulier les sommets de f (points de courbure extrémale) ;
• entre deux tels points, la tangente à la développée g au point de paramètre s est la normale à la courbe f.