Filtre à réponse impulsionnelle finie
En traitement du signal, un filtre à réponse impulsionnelle finie ou filtre RIF (en anglais Finite Impulse Response filter ou FIR filter) est un filtre dont la réponse impulsionnelle est de durée finie.
Cet article concerne le filtre de signal. Pour les autres significations du sigle, voir RIF.
Pour les articles homonymes, voir FIR.
On parle le plus souvent de filtre RIF pour des filtres à temps discret. Un filtre numérique RIF est caractérisé par une réponse uniquement basée sur un nombre fini de valeurs du signal d'entrée. Par conséquent, quel que soit le filtre, sa réponse impulsionnelle sera stable et de durée finie, dépendante du nombre de coefficients du filtre. Les termes de filtre non récursif ou de filtre à moyenne mobile sont parfois employés pour nommer la même classe de filtres, bien que l'expression de filtre à moyenne mobile désigne en premier lieu les filtres passe-bas.
Parmi les filtres linéaires, les filtres à réponse impulsionnelle finie sont opposés aux filtres à réponse impulsionnelle infinie (filtre RII) qui ne peuvent être réalisés que par une implémentation récursive.
Description
De façon générale le filtre à réponse impulsionnelle finie est décrit par la combinaison linéaire suivante où représente les valeurs du signal d'entrée et les valeurs du signal de sortie.
En utilisant le symbole de sommation, l'équation peut être réécrite de la façon suivante :
N = Nombre de coefficients (ordre du filtre)
bk = Coefficients de la fonction de transfert du filtre
C'est une convolution (discrète) entre le signal d'entrée et une fonction représentée par les valeurs , celles-ci décrivant ainsi la réponse impulsionnelle du filtre.
Puisque la réponse est une somme d'un nombre fini de valeurs, le filtre RIF est naturellement stable d'après le critère Entrée Bornée/Sortie Bornée.
Réalisation
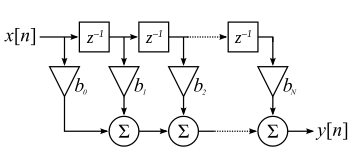
Les filtres numériques peuvent être réalisés à l'aide de trois éléments ou opérations de base. Soit l'élément gain, l'élément de sommation et le retard unitaire. Ces éléments sont suffisants pour réaliser tous les filtres numériques linéaires possibles. La réalisation présentée dans la figure ci-contre est une réalisation directe de type 1 du filtre RIF.
Des logiciels comme MATLAB ou GNU Octave proposent des fonctions pour la conception de ce genre de filtres[1],[2].
Propriétés
Les remarques générales suivantes peuvent être portées sur les filtres RIF.
- Les filtres RIF sont forcément stables, peu importe les coefficients utilisés.
- La complexité d'un filtre RIF est moindre que celle d'un filtre RII du même ordre. Cette propriété peut être utile sur les plateformes limitées en puissance de calcul.
- Généralement, les filtres RIF sont moins sensibles aux erreurs de quantification que les filtres RII. L'absence de récursivité empêche les erreurs cumulatives.
- Un filtre RIF est moins sélectif qu'un filtre RII du même ordre. C'est-à-dire que la transition entre la bande passante et la bande rejetée est moins rapide que dans le cas du filtre RII.
- Contrairement à un RII, un filtre RIF peut avoir une réponse impulsionnelle symétrique et introduire un retard sur le signal mais aucun déphasage.
Bibliographie
- (en) Ashock Ambardar, Analog and Digital Signal Processing, Brooks/Cole, 1999 (ISBN 053495409X)
Notes
- (en) « Digital Filter Design », sur mathworks.nl
- Note : remez() (d'après Eugène Yakovlevitch Remez) sous GNU Octave équivaut à firpm() (Parks-McCleland) sous MATLAB
Voir aussi
Articles connexes
- Processeur de signal numérique (DSP)
- Transformée en Z
- Algorithme de Savitzky-Golay
- Algorithme de Parks–McClellan (en)
Liens externes
- Les filtres RIF dans les radios logicielles https://sites.google.com/site/f4eyuradio/les-filtres-rif
- Portail de l’électricité et de l’électronique