Filtre médian
Le filtre médian est un filtre numérique non linéaire, souvent utilisé pour la réduction de bruit. La réduction de bruit est une étape de prétraitement classique visant à améliorer les résultats de traitements futurs (détection de bords par exemple). La technique de filtre médian est largement utilisée en traitement d'images numériques car il permet sous certaines conditions de réduire le bruit tout en conservant les contours de l'image.
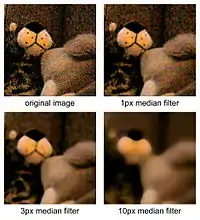
Principe
L'idée principale du filtre médian est de remplacer chaque entrée par la valeur médiane de son voisinage.
Par exemple, si on considère ces neuf pixels, dont une valeur aberrante (ici 111) :
| 5 | 6 | 7 |
| 6 | 111 | 8 |
| 7 | 8 | 9 |
le filtre médian va considérer les valeurs du voisinage par valeurs croissantes :
| 5 | 6 | 6 | 7 | 7 | 8 | 8 | 9 | 111 |
et prendre la valeur médiane, ici la valeur 7. La sortie du filtre donnera donc :
| 5 | 6 | 7 |
| 6 | 7 | 8 |
| 7 | 8 | 9 |
ce qui a permis de remplacer la valeur aberrante par une valeur « de consensus » entre les valeurs voisines.
Caractéristiques et utilisations

Le filtre médian permet d'éliminer les valeurs aberrantes sans se limiter à faire un calcul de moyenne qui aura tendance à contaminer les valeurs voisines avec cette valeur aberrante et flouter l'image.
Le filtre médian respecte le contraste de l'image (si on multiplie toutes les valeurs par une constante positive, l'ordonnancement des valeurs est inchangé) et la luminosité de l'image (ajouter une constante ne modifie pas l'ordonnancement non plus).
Dans les zones où l'intensité est monotone (uniquement croissante ou uniquement décroissante) le filtre laisse l'image inchangée. Il respecte les contours, et élimine les valeurs extrêmes.
En revanche la composition de plusieurs filtres médians ne correspond pas à un filtre médian [citation nécessaire].
Notes et références
- Pierre Bonnet, « Filtrage médian », sur Lagis à l'Université de Lille,
- Portail de l’imagerie numérique