Cosinus

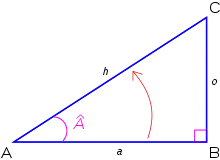
Pour définir le cosinus d'un angle Â, noté cos Â, considérons un triangle rectangle arbitraire qui contient l'angle Â.

Les côtés du triangle rectangle sont appelés :

• l’hypoténuse : c'est le côté opposé à l'angle droit, une jambe de l'angle  et le côté le plus long du triangle ;
• le côté opposé : c'est le côté opposé à l'angle  qui nous intéresse ;
• le côté adjacent : c'est le côté qui est une jambe de l'angle Â, qui n'est pas l'hypoténuse.

On notera :

h : la longueur de l'hypoténuse ;

a : la longueur du côté adjacent.

Alors :

${\displaystyle \cos({\widehat {A}})={\frac {c{\hat {o}}t{\acute {e}}\;adjacent}{hypot{\acute {e}}nuse}}={\frac {a}{h}}}$.

Ce rapport ne dépend pas du triangle rectangle particulier choisi, aussi longtemps qu'il contient l'angle, puisque tous ces triangles rectangles sont semblables.

${\displaystyle \cos(\omega )}$ est égal à la longueur du segment indiqué en noir. Le segment rouge indique un rayon du cercle.

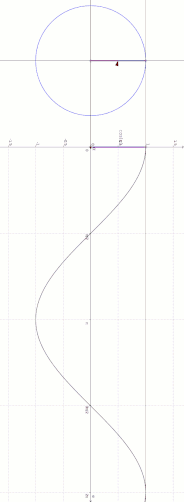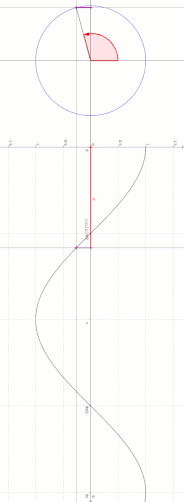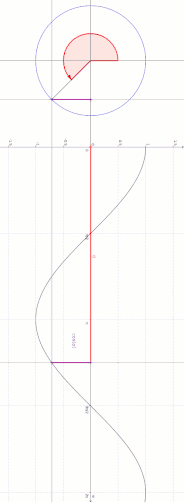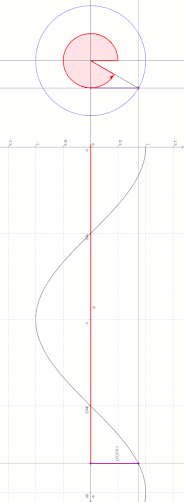
En trigonométrie, le cercle unité est le cercle de rayon 1 centré à l'origine (0, 0) d'un système de coordonnées cartésiennes.

Considérons l'intersection entre une droite passant par l'origine, faisant un angle ${\displaystyle \omega }$ avec la moitié positive de l'axe x, et le cercle unité. Alors la composante horizontale de cette intersection est égale à ${\displaystyle \cos(\omega )}$.

Animation montrant le graphique de y = cos(x) (où x est l'angle en radians) sur le cercle unité.

La fonction cosinus peut être définie à partir de la série entière, qui converge pour tout réel x :

${\displaystyle \cos x=\sum _{n=0}^{+\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}}$.

Autrement dit, le cosinus de x est défini comme la partie réelle de la série exponentielle de ix :

${\displaystyle \cos x={\frac {\operatorname {e} ^{\mathrm {i} x}+\operatorname {e} ^{-\mathrm {i} x}}{2}}}$.

Cette définition, jointe à celle analogue du sinus (comme partie imaginaire), est équivalente à la formule d'Euler.

La série entière précédente est l'unique solution du problème de Cauchy :

${\displaystyle y''=-y,\,y(0)=1,y'(0)=0}$,

qui constitue donc une définition équivalente de la fonction cosinus.

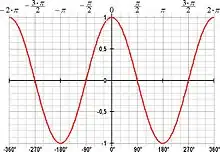
La fonction cosinus est périodique, de période 2π.

${\displaystyle \forall x\in \mathbb {R} \quad \cos(x+2\pi )=\cos x}$.

Cette propriété découle naturellement de la définition à partir du cercle unité (voir supra).

Plus précisément, deux nombres réels ont le même cosinus si et seulement si leur somme ou leur différence appartient à ${\displaystyle 2\pi \mathbb {Z} }$.

Une autre approche[1] consiste à partir de la série entière de l’exponentielle, et à montrer que cette fonction est périodique de période ${\displaystyle \mathrm {i} T}$ pour un certain ${\displaystyle T>0}$.

La fonction cosinus est paire :

${\displaystyle \forall x\in \mathbb {R} \quad \cos(-x)=\cos x}$.

Cette propriété apparaît clairement dans le développement en série entière.

La fonction cosinus est périodique donc non injective. Aussi, on considère sa restriction à [0, π] qui, elle, est bien bijective de [0, π] dans l'image [–1, 1], et l'on définit alors la fonction réciproque arc cosinus :

${\displaystyle {\begin{matrix}\mathrm {arccos}$ :&[-1,1]&\to &[0,\pi ]\\&x&\mapsto &\arccos x\end{matrix}}}

qui vérifie donc

${\displaystyle \forall x\in [0,\pi ]\quad \arccos(\cos x)=x}$ ;

${\displaystyle \forall x\in [-1,1]\quad \cos(\arccos x)=x}$.

La dérivée de la fonction cosinus est l'opposée de la fonction sinus :

${\displaystyle \forall x\in \mathbb {R} \quad \cos 'x=-\sin x}$.

Une primitive de cos est sin, ce qui s'écrit :

${\displaystyle \forall x\in \mathbb {R} \quad \sin 'x=\cos x}$.

Pour tout réel x, la fonction cosinus est continue au point x, donc sa limite en ce point est cos(x).

Du fait de sa périodicité, elle n'a pas de limite en ±∞.

Quelques angles communs (θ) sur le cercle unité. Les angles sont indiqués en degrés et en radians, ainsi que leur intersection avec le cercle unité (cos θ, sin θ).

Les valeurs figurant dans le tableau ci-dessous correspondent à des angles pour lesquels une expression à l'aide de racines carrées est possible, et plus précisément pour lesquels le théorème de Wantzel s'applique ; pour plus de détails, voir l'article Polynôme minimal des valeurs spéciales trigonométriques.

x (angle)			cos x
Degrés	Radians	Grades	Exacte	Décimale
0°	0	0g	1	1
180°	${\displaystyle \pi }$	200g	-1	-1
15°	${\displaystyle {\frac {\pi }{12}}}$	16 2⁄3g	${\displaystyle {\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}}$	0,965925826289068
165°	${\displaystyle {\frac {11\pi }{12}}}$	183 1/3g	${\displaystyle -{\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}}$	-0,965925826289068
30°	${\displaystyle {\frac {\pi }{6}}}$	33 1⁄3g	${\displaystyle {\frac {\sqrt {3}}{2}}}$	0,866025403784439
150°	${\displaystyle {\frac {5\pi }{6}}}$	166 2⁄3g	${\displaystyle -{\frac {\sqrt {3}}{2}}}$	-0,866025403784439
45°	${\displaystyle {\frac {\pi }{4}}}$	50g	${\displaystyle {\frac {\sqrt {2}}{2}}}$	0,707106781186548
135°	${\displaystyle {\frac {3\pi }{4}}}$	150g	${\displaystyle -{\frac {\sqrt {2}}{2}}}$	-0,707106781186548
60°	${\displaystyle {\frac {\pi }{3}}}$	66 2⁄3g	${\displaystyle {\frac {1}{2}}}$	0,5
120°	${\displaystyle {\frac {2\pi }{3}}}$	133 1⁄3g	${\displaystyle -{\frac {1}{2}}}$	-0,5
75°	${\displaystyle {\frac {5\pi }{12}}}$	83 1⁄3g	${\displaystyle {\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}}$	0,258819045102521
105°	${\displaystyle {\frac {7\pi }{12}}}$	116 2⁄3g	${\displaystyle -{\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}}$	-0,258819045102521
90°	${\displaystyle {\frac {\pi }{2}}}$	100g	0	0
36°	${\displaystyle {\frac {\pi }{5}}}$	40g	${\displaystyle {\frac {1+{\sqrt {5}}}{4}}}$	0,8090169944
54°	${\displaystyle {\frac {3\pi }{10}}}$	60g	${\displaystyle {\frac {\sqrt {10-2{\sqrt {5}}}}{4}}}$	0,5877852523
126°	${\displaystyle {\frac {7\pi }{10}}}$	140g

La racine de l'équation cos(x) = x est ipso facto un nombre remarquable, appelé le nombre de Dottie.

La fonction cosinus peut s'étendre sur le domaine complexe, où elle est une fonction entière :

${\displaystyle \forall z\in \mathbb {C} \quad \cos z=\sum _{n=0}^{+\infty }{\frac {(-1)^{n}z^{2n}}{(2n)!}}={\frac {\mathrm {e} ^{\mathrm {i} z}+\mathrm {e} ^{-\mathrm {i} z}}{2}}}$.

On a alors ${\displaystyle \cos z=\cos(\Re (z))\cosh(\Im (z))-\mathrm {i} \sin(\Re (z))\sinh(\Im (z))}$.

En particulier, pour ${\displaystyle y\in \mathbb {R} }$, on a ${\displaystyle \cos(\mathrm {i} y)=\cosh y}$, ce qui montre que sur l'axe imaginaire la fonction cosinus croît exponentiellement[2].