Fonction de Volterra

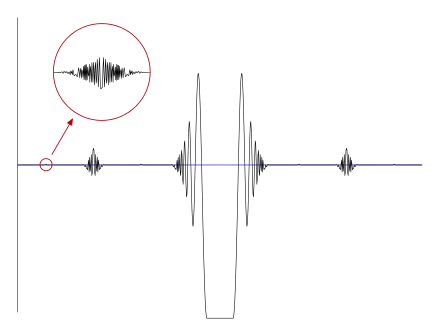
La fonction est définie à partir de l'ensemble de Smith-Volterra-Cantor, qui sera noté ici S, et des « copies » de la fonction ${\displaystyle f}$ définie par ${\displaystyle f(x)=x^{2}\sin \left({\frac {1}{x}}\right)}$ pour ${\displaystyle x}$ ≠ 0 et ${\displaystyle f(0)=0}$, le but étant de construire une fonction dérivable dont la dérivée est discontinue sur un ensemble de mesure non nulle[1]. Une telle dérivée ne pourra pas être Riemann-intégrable.

L'ensemble S est une partie fermée de [0,1], de mesure non nulle, d'intérieur vide, sans point isolé. Son complémentaire dans [0,1] est une réunion dénombrable d'intervalles ouverts. On définit la fonction de Volterra de la façon suivante. Elle est nulle sur S. Sur chaque intervalle ouvert ${\displaystyle ]a,b[}$ du complémentaire de S, elle est égale à une fonction dérivable, à dérivée continue, se prolongeant en a et en b en une fonction continue et dérivable, avec ${\displaystyle f(a)=f(b)=f'(a)=f'(b)=0}$, mais de façon que la dérivée soit discontinue en a et en b. Pour cela, on adapte à l'intervalle ${\displaystyle ]a,b[}$ la construction ci-dessous effectuée, pour simplifier les notations, au cas de l'intervalle ]0,1[ :

• Prendre ${\displaystyle f(x)=x^{2}\sin \left({\frac {1}{x}}\right)}$ pour ${\displaystyle x\in ]0,c]}$, avec c un réel élément de ${\displaystyle ]0,{\frac {1}{2}}]}$ et tel que ${\displaystyle f'(c)=0}$.
• Prendre ${\displaystyle f(x)=f(c)}$ sur ${\displaystyle [c,{\frac {1}{2}}]}$.
• Prendre ${\displaystyle f(x)=f(1-x)}$ sur ${\displaystyle [{\frac {1}{2}},1]}$.

Ayant effectué une construction comparable sur chaque intervalle du complémentaire de S, on obtient une fonction V dérivable en tout point de ${\displaystyle [0,1]}$, et dont la dérivée est discontinue sur S et continue sur son complémentaire[1].

En effet, la fonction f précédente est dérivable en 0, de dérivée nulle. Mais pour x non nul, on a ${\displaystyle f'(x)=2x\sin(1/x)-\cos(1/x)}$, ce qui implique que dans tout voisinage de zéro, il y a des points où ${\displaystyle f'(x)}$ prend les valeurs 1 et -1. Ainsi, il y a des points où ${\displaystyle V'(x)}$ prend les valeurs 1 et -1 dans tout voisinage de chaque borne des intervalles retirés lors de la construction de l'ensemble S de Smith-Volterra-Cantor. Ainsi, en tout point de S, V est dérivable, de dérivée nulle, mais ${\displaystyle V'(x)}$ y est discontinue. Cependant, ${\displaystyle V'}$ est continue dans chacun de ces intervalles, donc l'ensemble des points de discontinuités de ${\displaystyle V'}$ est exactement égal à S.

Comme l'ensemble S admet une mesure de Lebesgue strictement positive, cela signifie que ${\displaystyle V'}$ est discontinue sur un ensemble de mesure non nulle, et donc non Riemann-intégrable[2]^,[3].

Notons que si l'on avait mené la même construction sur l'ensemble de Cantor C, on aurait obtenu une fonction avec des propriétés similaires, mais la dérivée aurait été discontinue sur C qui est de mesure nulle, et la fonction obtenue aurait alors eu une dérivée Riemann-intégrable.

• Portail de l'analyse