Fonction de couplage

En mathématiques, une fonction de couplage, est une méthode permettant d’attribuer de manière unique un entier naturel à un couple d'entiers naturels.

En théorie des ensembles, on peut utiliser n'importe quelle fonction de couplage pour prouver que l'ensemble des entiers relatifs et celui des nombres rationnels ont la même cardinalité que l'ensemble des entiers naturels. En théorie de la calculabilité, la fonction de couplage de Cantor est utilisée pour coder k-uplets, ainsi une fonction de $N k \to N$ peut être représentée par une fonction de $N \to N$ .

Définition

Une fonction de couplage est une bijection calculable de $N \times N$ dans $N$ .

Fonction de couplage de Cantor

Numérotation des éléments de N x N par la fonction de couplage de Cantor.

La fonction de couplage de Cantor ${\displaystyle \pi$ est définie par

\pi (x,y):={\frac {(x+y+1)(x+y)}{2}}+y.

Le théorème de Fueter-Pólya énonce que cette fonction est, avec la fonction $(x,y)\mapsto \pi (y,x)$ , la seule fonction de couplage quadratique. En revanche, savoir s'il s'agit de la seule fonction polynomiale de couplage est encore une question ouverte. On note parfois $\langle x,y\rangle$ le résultat de la fonction de couplage sur les entrées $x$ et $y$ .

La fonction de Cantor peut être généralisée de la manière suivante :

\pi ^{(n)}:\mathbb {N} ^{n}\to \mathbb {N}

avec

\pi ^{(n)}(k_{1},\ldots ,k_{n-1},k_{n}):=\pi (\pi ^{(n-1)}(k_{1},\ldots ,k_{n-1}),k_{n}).

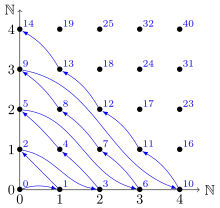
Construction graphique

Cette autre progression en diagonale, analogue mais différente de celle de la fonction de Cantor, fournit une autre fonction de couplage. Ici elle est utilisée pour prouver la dénombrabilité des nombres rationnels.

La fonction de couplage de Cantor est définie en parcourant $\mathbb {N} ^{2}$ par diagonales successives.

En suivant l'énumération diagonale par diagonale La fonction de couplage de Cantor vérifie :

\pi (0,0)=0

;

\pi (x+1,0)=\pi (0,x)+1

;

\pi (x,y+1)=\pi (x+1,y)+1

;

ce qui fournit une définition récursive de la fonction (le couple (x + y, x) décroît strictement à chaque appel récursif pour l'ordre lexicographique ).

Pour tout $t\in \mathbb {N}$ , la diagonale d'équation $x+y=t$ contient $t+1$ points (de $(t,0)$ à $(0,t)$ ). Le nombre de points des diagonales qui précèdent celle du couple $(x,y)$ est donc égal à $\sum _{0\leq t<x+y}(t+1)=\sum _{1\leq s\leq x+y}s={\frac {(x+y)(x+y+1)}{2}}$ (le $(x+y)$ -ième nombre triangulaire). Par conséquent l'image du couple $(x,y)$ est donnée par :

\pi (x,y)={\frac {(x+y)(x+y+1)}{2}}+y

.

Bijection réciproque

D'après la construction ci-dessus, $\pi$ est bijective, c'est-à-dire que pour tout $z\in \mathbb {N}$ , il existe un unique couple $(x,y)\in \mathbb {N} ^{2}$ tel que $z=\pi (x,y)$ .

Retrouvons-le par analyse-synthèse en cherchant $(x,y,w)\in \mathbb {N} ^{3}$ tel que $w=x+y$ et ${\frac {w(w+1)}{2}}+y=z$ .

Ces deux équations impliquent

{\frac {w(w+1)}{2}}\leq z<{\frac {w(w+1)}{2}}+w+1={\frac {w(w+3)}{2}}+1={\frac {(w+1)(w+2)}{2}}

,

donc $w$ est nécessairement l'unique entier naturel tel que

z\in \left[{\frac {w(w+1)}{2}},{\frac {(w+1)(w+2)}{2}}\right[

,

puis $y=z-{\frac {w(w+1)}{2}}$ et $x=w-y$ , ce qui prouve l'injectivité.

Réciproquement, le triplet $(x,y,w)\in \mathbb {N} ^{3}$ ainsi construit à partir de $z$ vérifie bien les deux équations, ce qui prouve la surjectivité.

La bijection réciproque de $\pi$ est donc donnée par :

\pi ^{-1}(z)=\left({\frac {w(w+3)}{2}}-z,z-{\frac {w(w+1)}{2}}\right)

avec

w

égal à la partie entière du réel

w':={\frac {-1+{\sqrt {1+8z}}}{2}}

(solution de l'équation du second degré

z={\frac {w'(w'+1)}{2}}

).

Autres fonctions de couplage

Via le bon ordre canonique sur ℕ×ℕ

Bon ordre sur ℕ² et bijection ℕ²→ℕ

On rencontre fréquemment[1] la méthode suivante pour démontrer que $\kappa ^{2}=\kappa$ (où $\kappa$ est un cardinal infini : un bon ordre est défini sur $\kappa \times \kappa$ dont chaque éléments possède ${}<\kappa$ prédécesseurs, de sorte que $\kappa \times \kappa$ et $\kappa$ sont isomorphes comme ensembles ordonnés et sont donc équipotents. Dans le cas plus simple où $\kappa =\mathbb {N}$ cette méthode conduit à une bijection $\mathbb {N} ^{2}\to \mathbb {N}$ .

Définissons sur $\mathbb {N} \times \mathbb {N}$ la relation binaire

$(k,\ell )\preccurlyeq (m,n)$ si ${\begin{cases}{\text{ou bien}}\ (k,\ell )=(m,n),\\[3pt]{\text{ou bien}}\ \max(k,\ell )<\max(m,n),\\[3pt]{\text{ou bien}}\ \max(k,\ell )=\max(m,n)\ {\text{et}}\ k<m,\\[3pt]{\text{ou bien}}\ \max(k,\ell )=\max(m,n)\ {\text{et}}\ k=m\ {\text{et}}\ l<n.\end{cases}}$

Alors $\preccurlyeq$ est une relation de bon ordre pour laquelle chaque élément possède un nombre fini de minorants. On définit une bijection $\mathbb {N} \to \mathbb {N} ^{2}$ par récurrence :

$c_{0}=\min \nolimits _{\preccurlyeq }(\mathbb {N} ^{2})=(0,0)$ ;

$c_{\lambda +1}$ est le $\preccurlyeq$ -successeur de $c_{\lambda }$ , c'est-à-dire $\min \nolimits _{\preccurlyeq }{\bigl (}\mathbb {N} ^{2}\smallsetminus \{c_{i}\mid i\leqslant \lambda \}{\bigr )}$ .

Démonstration

Donnons un nom aux « lignes de niveau » de la fonction $\max({}\mathbin {\cdot } {},{}\mathbin {\cdot } {})$ : pour $a\in \mathbb {N}$ , soit $L_{a}=\{(m,n)\mid \max(m,n)=a\}$ .
On a les faits suivants :
– la suite $(L_{a})_{a\in \mathbb {N} }$ est une partition de $\mathbb {N}$ ;
– on a la partition $L_{a}=H_{a}\cup V_{a}$ , où $H_{a}=\{(0,a),\dots ,(a-1,a)\}$ et $V_{a}=\{(a,0),\ldots ,(a,a)\}$ ;
– $L_{a}$ est un ensemble fini de cardinal $2a+1$ ;
– la restriction de $\preccurlyeq$ à $L_{a}$ est une relation d'ordre total : les éléments de $H_{a}$ sont rangés par abscisse croissante, ceux de $V_{a}$ par ordonnée croissante et chaque élément de $H_{a}$ est inférieur à chaque élément de $V_{a}$ ;
– par ailleurs si $a<a'$ et $(c,c')\in L_{a}\times L_{a'}$ alors $c\prec c'$ .

La relation $\preccurlyeq$ est réflexive par définition.
Supposons $c\preccurlyeq c'$ et $c'\preccurlyeq c$ . On a $(c,c')\in L_{a}\times L_{a'}$ (où $a,a'\in \mathbb {N}$ ). Si on avait par exemple $a<a'$ alors aucune des quatre conditions définissant $c'\preccurlyeq c$ ne serait satisfaite : il faut donc que $a'\leqslant a$ et, par symétrie, $a\leqslant a'$ donc $a=a'$ . Mais alors $\preccurlyeq _{\upharpoonright L_{a}}$ étant un ordre total, son antisymétrie implique $c=c'$ . La relation $\preccurlyeq$ est donc antisymétrique.
Supposons $c\preccurlyeq c'$ et $c'\preccurlyeq c''$ . On a $(c,c',c'')\in L_{a}\times L_{a'}\times L_{a''}$ (où $a,a',a''\in \mathbb {N}$ ). Sans perdre en généralité on peut supposer que $a\leqslant a'\leqslant a''$ et on conclut, en examinant les quatre cas possibles d'inégalités $(\leqslant ,\leqslant )=(<,<)$ ou $(=,<)$ ou $(<,=)$ ou $(=,=)$ , que $c\preccurlyeq c''$ . La relation $\preccurlyeq$ est donc transitive.
La relation $\preccurlyeq$ est donc bien un ordre. Si $X\subset \mathbb {N} ^{2}$ est non vide alors l'ensemble $\{a\in \mathbb {N} \mid X\cap L_{a}\neq \varnothing \}$ est non vide et admet un plus petit élément $a_{0}$ ; mais alors le plus petit élément de $X\cap L_{a_{0}}$ minore tous les éléments de $X$ , de sorte que $(\mathbb {N} ^{2},\preccurlyeq )$ est bien ordonné.
Si $c\in L_{a}$ l'ensemble des minorants de $c$ est inclus dans la réunion $\textstyle \bigcup _{0\leqslant i\leqslant a}L_{i}$ , qui est finie.

La définition par récurrence donnée plus haut fournit donc une suite $(c_{\lambda })_{\lambda \in \mathbb {N} }$ qui est une énumération strictement croissante de $\mathbb {N} ^{2}$ .

On observe que, pour $a>0$ , l'ensemble des minorants stricts de $(0,a)$ est exactement $[0,a-1]\times [0,a-1]$ , qui est de cardinal $a^{2}$ , de sorte que $(0,a)=c_{a^{2}}$ .
Ensuite, pour $(b,a)\in H_{a}$ on a $(b,a)=c_{a^{2}+b}$ (par récurrence sur $b\in [0,a-1]$ ) ; notamment $(a-1,a)=c_{a^{2}+a-1}$ , lequel a pour successeur $c_{a^{2}+a}=(a,0)\in V_{a}$ .
Enfin pour $(a,b)\in V_{a}$ , on a $(a,b)=c_{a^{2}+a+b}$ (par récurrence sur $b\in [0,a]$ ).

Ceci se résume en $\forall (a,b)\in \mathbb {N} ^{2}\quad (a,b)={\begin{cases}c_{a+b^{2}}&{\text{si}}\ a<b,\\[3pt]c_{a^{2}+a+b}&{\text{si}}\ a\geqslant b.\end{cases}}$

Via une propriété arithmétique élémentaire

Une autre méthode consiste à utiliser la propriété arithmétique suivante : tout entier $n\geqslant 1$ peut s'écrire d'une façon unique sous la forme du produit d'une puissance de 2 par un nombre impair, soit $n=2^{a}(2b+1)$ , où $a,b\in \mathbb {N}$ . L'application $f\colon \mathbb {N} ^{2}\longrightarrow \mathbb {N}$ définie par $f(a,b)=2^{a}(2b+1)-1$ est ainsi une bijection.

Via l'écriture d'un nombre entier en base 2

Bourbaki utilise une injection $\mathbb {N} \times \mathbb {N} \to \mathbb {N}$ , afin de prouver l'équipotence de ces deux ensembles, dans le volume I des Éléments de mathématiques (III §6). Il s'avère que c'est une bijection.
Tout $n\in \mathbb {N}$ possède une unique écriture en base 2 $n={\overline {a_{r}\ldots a_{0}}}$ (où $a_{r},\ldots ,a_{0}\in \{0,1\}$ sont les chiffres de l'écriture de $n$ ), c'est-à-dire : $\textstyle n=\sum _{k=0}^{r}a_{k}2^{k}$ . On observe que si $n>0$ alors $a_{r}=1$ , et si $n=0$ alors $r=0$ et $n={\overline {0}}$ .
À l'entier $n$ on fait correspondre la suite $\varphi (n)=(\phi _{i})_{i\in \mathbb {N} }$ définie par $\phi _{i}={\begin{cases}a_{i}&{\text{si}}\ i\leqslant r,\\[3pt]0&{\text{si}}\ i>r.\end{cases}}$
Dit autrement $\varphi (n)$ est la suite infinie de 0 et de 1 qui commence par énumérer les chiffres de $n$ dans l'ordre inverse de leur écriture puis se poursuit par une infinité de 0, soit $(a_{0},\ldots ,a_{r},\mathbf {0} ,\dots )$ . L'application $\varphi$ est une bijection $\mathbb {N} \colon \to {\mathfrak {N}}$ := le sous-ensemble de $\{0,1\}^{\mathbb {N} }$ constitué des suites presque nulles (et $\textstyle \varphi ^{-1}{\bigl (}(a_{i})_{i\in \mathbb {N} }{\bigr )}=\sum _{i}a_{i}2^{i}$ ).

Par ailleurs, si $\mathbf {x} =(x_{i})_{i\in \mathbb {N} },\;\mathbf {y} =(y_{i})_{i\in \mathbb {N} }\in {\mathfrak {N}}$ on définit $\mathbf {z} =\psi [\mathbf {x} ,\mathbf {y} ]$ par $z_{2i}=x_{i}$ et $z_{2i+1}=y_{i}$ pour tout $i\in \mathbb {N}$ .
L'application $\psi$ est évidemment une bijection ${\mathfrak {N}}^{2}\to {\mathfrak {N}}$ .

En conclusion $f\colon (m,n)\longmapsto \varphi ^{-1}{\bigl (}\psi [\varphi (m),\varphi (n)]{\bigr )}$ est une bijection $\mathbb {N} ^{2}\to \mathbb {N}$ .

Donnons un exemple : $(m,n)=(13,18)$ . On a $m={\overline {1101}},\ n={\overline {\color {RoyalBlue}10010}}$ ; alors

\psi [\varphi (m),\varphi (n)]=(1,{\color {RoyalBlue}0},0,{\color {RoyalBlue}1},1,{\color {RoyalBlue}0},1,{\color {RoyalBlue}0},0,{\color {RoyalBlue}1},\mathbf {0} ,\ldots )=\varphi (2^{0}+2^{3}+2^{4}+2^{6}+2^{9})=\varphi (601).

Donc $f(13,18)=601$ .

Inversement, partant de $\ell =347={\overline {1{\color {RoyalBlue}0}1{\color {RoyalBlue}0}1{\color {RoyalBlue}1}0{\color {RoyalBlue}1}1}}$ , on a

\varphi (\ell )=(1,{\color {RoyalBlue}1},0,{\color {RoyalBlue}1},1,{\color {RoyalBlue}0},1,{\color {RoyalBlue}0},1,\mathbf {0} ,\ldots )=\psi [(1,0,1,1,1,\mathbf {0} ,\ldots )\mathbin {,} ({\color {RoyalBlue}1},{\color {RoyalBlue}1},{\color {RoyalBlue}0},{\color {RoyalBlue}0},\mathbf {0} ,\ldots )]=\psi [\varphi (29),\varphi (3)].

Donc $347=f(29,3)$ .

L'analogue de la fonction $f$ en base 10 — notons-la $g$ — est plus maniable puisqu'elle évite les allers-retours entre les bases 2 et 10.

Par exemple $\definecolor {rouge}{rgb}{0.5,0,0}g(68\,042\mathbin {,} {\color {rouge}59\,713})={\color {rouge}5}\,6{\color {rouge}9}8\,{\color {rouge}7}0{\color {rouge}1}\,4{\color {rouge}3}2$ ; inversement $\definecolor {rouge}{rgb}{0.5,0,0}g^{-1}(1{\color {rouge}0}\,3{\color {rouge}5}7)=(137\mathbin {,} {\color {rouge}5})$ .

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Pairing function » (voir la liste des auteurs).

Voir par exemple (en) Kenneth Kunen, Set theory : An Introduction to Independence Proofs, vol. 102, North-Holland, coll. « Studies in Logic and the Foundations of Mathematics », 1980 (réimpr. 1983, 1988 et 1990) (ISBN 0444868399), p. 29.

Bibliographie

Nicolas Bourbaki, Théorie des ensembles, vol. 1, Hermann, 1970 (ISBN 978-3-540-34034-8)

Voir aussi

Article connexe

Déployeur universel

Liens externes

(en) Steven Pigeon, « Pairing function », sur MathWorld
(en) Matthew Szudzik, « An Elegant Pairing Function », Wolfram Research, 2006

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Voir par exemple (en) Kenneth Kunen, Set theory : An Introduction to Independence Proofs, vol. 102, North-Holland, coll. « Studies in Logic and the Foundations of Mathematics », 1980 (réimpr. 1983, 1988 et 1990) (ISBN 0444868399), p. 29.