Fonction de distribution radiale

Si une particule donnée est considérée comme étant à l'origine O, et si ρ est la densité moyenne en nombre des particules, alors la densité moyenne locale en fonction du temps à une distance ${\displaystyle r}$ de O est ${\displaystyle \rho g(r)}$. Cette définition simplifiée est valable pour un système homogène et isotrope. Un cas plus général sera examiné ci-dessous.

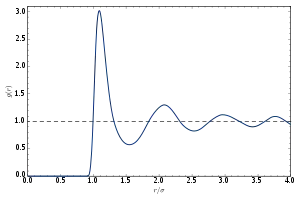
En termes plus simples, il s'agit d'une mesure de la probabilité de trouver une particule à une distance r d'une particule de référence donnée, par rapport à celle d'un gaz idéal. L'algorithme général implique de déterminer combien de particules se trouvent entre les distances ${\displaystyle r}$ et ${\displaystyle r+dr}$ par rapport à la particule de référence. Ce thème général est représenté à droite, où la particule rouge est notre particule de référence, et les particules bleues sont celles qui se trouvent dans la coquille circulaire, pointillées en orange.

La fonction de distribution radiale est généralement déterminé en calculant la distance entre toutes les paires de particules et en les séparant en un histogramme. L'histogramme est alors normalisé par rapport à un gaz idéal, où les histogrammes de particules sont complètement non corrélés. Pour trois dimensions, cette normalisation est la densité de nombre du système multipliée par le volume de la coquille sphérique, ce qui mathématiquement peut être exprimé comme ${\displaystyle g(r)_{I}=4\pi r^{2}\rho dr}$, où ${\displaystyle \rho }$ est la densité du nombre.

La fonction de distribution radiale peut être calculée soit à l'aide de méthodes de simulation par ordinateur, comme par la méthode de Monte Carlo, soit par l'équation d'Ornstein-Zernike, en utilisant des relations de fermeture approximatives comme l'approximation Percus-Yevick ou l'équation de la chaîne hypernettée. Il peut également être déterminé expérimentalement, par des techniques de diffusion de rayonnement ou par visualisation directe pour des particules de taille micrométrique suffisante par microscopie traditionnelle ou confocale.

La fonction de distribution radiale est d'une importance fondamentale car elle peut être utilisée, en utilisant la théorie de la solution de Kirkwood-Buff (en), pour relier les détails microscopiques aux propriétés macroscopiques. De plus, par la réversion de la théorie de Kirkwood-Buff, il est possible d'obtenir les détails microscopiques de la fonction de répartition radiale à partir des propriétés macroscopiques.