Formule de Mollweide
Les formules de Mollweide, nommées d'après le mathématicien et astronome prussien Carl Brandan Mollweide (de) (1774-1825), sont les identités trigonométriques suivantes en géométrie du triangle[1],[2] :
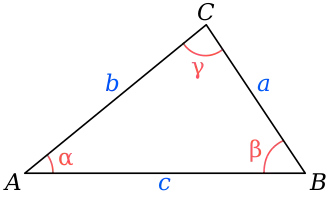
Notations usuelles pour un triangle.
où (cf. figure ci-contre) a, b et c désignent les longueurs des côtés d'un triangle ABC et α, β et γ les mesures des angles opposés.
La loi des tangentes en est un corollaire immédiat, compte tenu du fait que γ2 est complémentaire de α + β2 (donc le cosinus de l'un est égal au sinus de l'autre).
Démonstration
On utilise la loi des sinus, puis une formule de Simpson au numérateur et une formule de l'angle double au dénominateur :
ce qui prouve la première formule. La seconde se démontre de même.
Références
- (en) Ernest J. Wilczynski (de), Plane Trigonometry and Applications, Allyn & Bacon, 1914, p. 102.
- (en) Michael Sullivan, Trigonometry, Dellen Publishing Company, 1988, p. 243.
Voir aussi
Lien externe
(en) « Mollweide's formula : A proof », sur math.stackexchange
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.