Loi des tangentes

En géométrie du triangle, la loi des tangentes est une relation entre la longueur de deux côtés d'un triangle et la mesure de deux de ses angles.

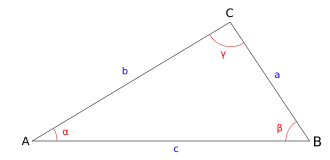
Fig. 1 - Notations usuelles dans un triangle quelconque.

On considère un triangle quelconque ABC, représenté sur la Fig. 1 ci-contre, où les angles sont désignés par α, β, γ et les côtés opposés aux angles par les lettres correspondantes a, b et c. Alors,

Démonstration

La loi des tangentes est un corollaire immédiat des formules de Mollweide.

On peut aussi la déduire directement, comme ces dernières, de la loi des sinus et des formules de Simpson :

Une variante pour la deuxième étape est :

Généralisation aux géométries non euclidiennes
Cette section ne cite pas suffisamment ses sources (février 2016). 
Pour l'améliorer, ajoutez des références de qualité et vérifiables (comment faire ?) ou le modèle {{Référence nécessaire}} sur les passages nécessitant une source.

Pour une surface non euclidienne de courbure K, on définit le rayon de courbure ρ par :

puis les dimensions réduites a, b et c du triangle par :

Géométrie sphérique
Fig. 2 - Triangle sphérique : dimensions réduites a, b et c ; angles α, β et γ.

Dans un triangle sphérique ABC, a, b et c correspondent à la mesure angulaire des segments de grand arc [BC], [AC] et [AB] (Fig. 2) et la loi des tangentes devient :

Notes et références

    Voir aussi
    • Portail de la géométrie
    Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.