Algorithme de Gauss-Newton

Soit m fonctions ${\displaystyle r_{i}}$ (${\displaystyle i=1,\ldots ,m}$) de n variables ${\displaystyle {\boldsymbol {\beta }}=(\beta _{1},\beta _{2},\dots ,\beta _{n}),}$ avec m≥n, l'algorithme de Gauss–Newton doit trouver le minimum de la somme des carrés[1] :

${\displaystyle S({\boldsymbol {\beta }})=\sum _{i=1}^{m}r_{i}^{2}({\boldsymbol {\beta }}).}$

En supposant une valeur initiale β⁰ du minimum, la méthode procède par itérations:

${\displaystyle {\boldsymbol {\beta }}^{s+1}={\boldsymbol {\beta }}^{s}+\delta {\boldsymbol {\beta }},}$

où l'incrément δβ vérifie les équations normales

${\displaystyle \left(\mathbf {J_{r}^{T}J_{r}} \right)\delta {\boldsymbol {\beta }}=-\mathbf {J_{r}^{T}r} .}$

Ici, on note par r le vecteur des fonctions r_i, et par J_r la matrice jacobienne m × n de r par rapport à β, tous les deux évalués en β^s. La matrice transposée est notée à l'aide de l'exposant T.

Dans les problèmes d'ajustement des données, où le but est de trouver les paramètres β d'un certain modèle y = f(x , β) permettant le meilleur ajustement aux observations (x_i, y_i), les fonctions r_i sont les résidus

${\displaystyle r_{i}({\boldsymbol {\beta }})=y_{i}-f_{i}(x_{i},{\boldsymbol {\beta }})}$

En notant f le vecteur des fonctions ${\displaystyle f_{i}(x_{i},{\boldsymbol {\beta }})}$, alors l'incrément δβ peut s'exprimer en fonction de la jacobienne de f (et du vecteur r) :

${\displaystyle \left(\mathbf {J_{f}^{T}} \mathbf {J_{f}} \right)\delta {\boldsymbol {\beta }}=\mathbf {J_{f}^{T}r} .}$

Dans tous les cas, une fois connue l'estimation à l'étape s, les équations normales permettent de trouver l'estimation à l'étape suivante ; pour résumer, on a :

${\displaystyle {\boldsymbol {\beta }}^{s+1}={\boldsymbol {\beta }}^{s}-\left(\mathbf {J_{r}^{T}J_{r}} \right)^{-1}\mathbf {J_{r}^{T}r} }$

L'ensemble du terme de droite est calculable car ne dépend que de β^s et permet de trouver l'estimation suivante.

L'hypothèse m ≥ n est nécessaire, car dans le cas contraire la matrice J_r^TJ_r serait non inversible et les équations normales ne pourraient être résolues.

L'algorithme de Gauss–Newton peut être dérivé par approximation linéaire du vecteur de fonctions r_i. En utilisant le théorème de Taylor, on peut écrire qu'à chaque itération

${\displaystyle \mathbf {r} ({\boldsymbol {\beta }}_{0})\approx \mathbf {r} ({\boldsymbol {\beta }}^{s})+\mathbf {J_{r}} ({\boldsymbol {\beta }}^{s})\delta {\boldsymbol {\beta }}}$

avec δβ = δβ - β^s ; notons que β₀ représente la vraie valeur des paramètres pour laquelle les résidus r(β₀) s'annulent. Trouver l'incrément δβ revient à résoudre

${\displaystyle -\mathbf {r} ({\boldsymbol {\beta }}^{s})\approx \mathbf {J_{r}} ({\boldsymbol {\beta }}^{s})\delta {\boldsymbol {\beta }}}$

ce qui peut se faire par la technique classique de régression linéaire et qui fournit exactement les équations normales.

Les équations normales sont un système de m équations linéaires d'inconnue δβ. Ce système peut se résoudre en une étape, en utilisant la factorisation de Cholesky ou, encore mieux, la décomposition QR de J_r. Pour de grands systèmes, une méthode itérative telle que la méthode du gradient conjugué peut être plus efficace. S'il existe une dépendance linéaire entre les colonnes J_r, la méthode échouera car J_r^TJ_r deviendra singulier.

Notons enfin que la méthode de Gauss-Newton est efficace lorsque l'erreur quadratique finale est faible, ou bien lorsque la non-linéarité est « peu prononcée »[2]. La méthode est en particulier sensible à la présence de points « aberrants » (c'est-à-dire situés loin de la courbe modèle).

Courbe calculée avec ${\displaystyle {\hat {\beta }}_{1}=0.362}$ et ${\displaystyle {\hat {\beta }}_{2}=0.556}$ (en bleu) contre les données observées (en rouge).

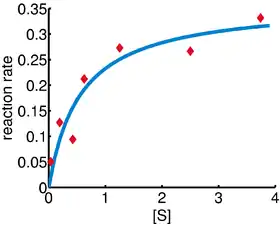
Dans cet exemple, l'algorithme de Gauss–Newton est utilisé pour ajuster un modèle en minimisant la somme des carrés entre les observations et les prévisions du modèle.

Dans une expérience de biologie, on étudie la relation entre la concentration du substrat [S] et la vitesse de réaction (rate) dans une réaction enzymatique à partir de données reportées dans le tableau suivant.

i	1	2	3	4	5	6	7
[S]	0.038	0.194	0.425	0.626	1.253	2.500	3.740
rate	0.050	0.127	0.094	0.2122	0.2729	0.2665	0.3317

On souhaite ajuster les données à la courbe de la forme :

${\displaystyle {\text{rate}}={\frac {V_{\max }[S]}{K_{M}+[S]}}}$

L'estimation par moindres carrés porte sur les paramètres ${\displaystyle V_{\max }}$ et ${\displaystyle K_{M}}$.

On note ${\displaystyle x_{i}}$ et ${\displaystyle y_{i}}$ les valeurs de [S] et la vitesse de réaction, pour ${\displaystyle i=1,\dots ,7.}$ On pose ${\displaystyle \beta _{1}=V_{\max }}$ et ${\displaystyle \beta _{2}=K_{M}.}$ On cherche donc les valeurs de ${\displaystyle \beta _{1}}$ et ${\displaystyle \beta _{2}}$ qui minimisent la somme des carrés des résidus

${\displaystyle r_{i}=y_{i}-{\frac {\beta _{1}x_{i}}{\beta _{2}+x_{i}}}}$   (${\displaystyle i=1,\dots ,7}$)

La jacobienne ${\displaystyle \mathbf {J_{r}} }$ du vecteur des résidus ${\displaystyle r_{i}}$ par rapport aux inconnus ${\displaystyle \beta _{j}}$ est une matrice ${\displaystyle 7\times 2}$ dont la ligne n° i est

${\displaystyle {\frac {\partial r_{i}}{\partial \beta _{1}}}=-{\frac {x_{i}}{\beta _{2}+x_{i}}},\ {\frac {\partial r_{i}}{\partial \beta _{2}}}={\frac {\beta _{1}x_{i}}{\left(\beta _{2}+x_{i}\right)^{2}}}.}$

On initialise par une estimation ${\displaystyle \beta _{1}=0,9;\beta _{2}=0,2}$. Il suffit alors de cinq itérations de l'algorithme de Gauss–Newton pour atteindre les estimations optimales ${\displaystyle {\hat {\beta }}_{1}=0,362}$ et ${\displaystyle {\hat {\beta }}_{2}=0,556}$. Le critère de la somme des carrés des résidus chute de 1,202 à 0,0886 en 5 itérations. Le tableau suivant détaille les cinq itérations :

Itération	Estimation	Somme des carrés des résidus
1	[0,9;0,2]	1,4455000
2	[0,33266;0,26017]	0,0150721
3	[0,34281;0,42608]	0,0084583
4	[0,35778;0,52951]	0,0078643
5	[0,36141;0,55366]	0,0078442
6	[0,3618;0,55607]	0,0078440

La figure ci-contre permet de juger de l'adéquation du modèle aux données en comparant la courbe ajustée (bleue) aux observations (rouge).

Lissage et dérivation par Savitzky-Golay, permettant d'obtenir les paramètres initiaux du modèle.

Ajustement d'un modèle de pic dissymétrique. Cliquer sur l'image pour voir le code source Scilab.

Étapes de l'algorithme lorsque l'on part de valeurs très éloignées : courbe ajustée (haut) et évolution de l'écart quadratique normalisé (bas).

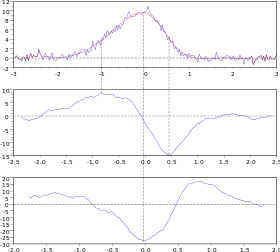
Dans un deuxième exemple, on essaie d'approcher une mesure de spectrométrie ou de diffractométrie présentant un pic dissymétrique, avec un bruit, par un modèle de pic dissymétrique composé de deux demi-gaussiennes ayant la même position (espérance) et la même hauteur, mais des « largeurs » (écarts types) différents : la fonction modèle est de la forme

${\displaystyle \left\{{\begin{aligned}f(x)=\ &\mathrm {A} (2)\times \exp \left({\frac {(x-\mathrm {A} (1))^{2}}{\mathrm {A} (3)}}\right){\text{ si }}x\leqslant \mathrm {A} (1){\text{$ ; }}\\f(x)=\ &\mathrm {A} (2)\times \exp \left({\frac {(x-\mathrm {A} (1))^{2}}{\mathrm {A} (4)}}\right){\text{ si }}x\geqslant \mathrm {A} (1){\text{.}}\end{aligned}}\right.}

La régression consiste à ajuster les paramètres A(1), A(2), A(3) et A(4).

Dans un premier temps, on détermine numériquement la dérivée et la dérivée seconde pour obtenir les paramètres initiaux du pic, avec l'algorithme de Savitzky-Golay :

• sommet de la courbe estimé par le minimum de la dérivée seconde, A(1) = -0,03 ;
• valeur de la courbe lissée à cet endroit : A(2) = 9,7 ;
• demi-largeur à mi-hauteur à gauche valant h_g = (0,84 - 0,03) (à partir de la position du point d'inflexion) ;
• demi-largeur à mi-hauteur à droite valant h_d = (0,45 + 0,03).

Pour une gaussienne pure, la demi-largeur à mi-hauteur h est reliée à l'écart type σ par :

${\displaystyle 2h=2,35\times \sigma }$

et l'on a

${\displaystyle A(3,4)=2\sigma ^{2}}$,

soit

${\displaystyle A(3,4)=8(h_{g,d}/2,35)^{2}}$.

L'algorithme converge en 5 étapes (variation de l'écart quadratique normalisé inférieur à 10⁻⁷) avec les résultats suivants :

• A(1) = 0,00404, pour une valeur théorique 0 ;
• A(2) = 9,83, " 10 ;
• A(3) = 1,02, " 1 ;
• A(4) = 0,313, " 0,3.

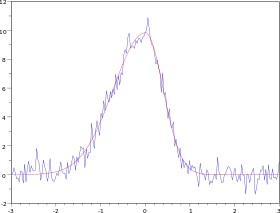
Sur la figure ci-contre, les points expérimentaux (au nombre de 200) forment la courbe bleue, le modèle ajusté est représenté par la courbe rouge.

Si l'on part du jeu de paramètres initiaux arbitraire [1, 1, 1, 1], l'algorithme converge en dix étapes à condition d'utiliser un facteur d'amortissement α ajusté automatiquement à chaque étape (voir ci-après).

On peut démontrer que l'incrément ${\displaystyle \delta \beta }$ est une direction de descente pour S[3], et que si l'algorithme converge, alors la limite est un point stationnaire pour la somme des carrés S. Toutefois, la convergence n'est pas garantie, pas plus qu'une convergence locale contrairement à la méthode de Newton.

La vitesse de convergence de l'algorithme de Gauss–Newton peut approcher la vitesse quadratique[4]. L'algorithme peut converger lentement voire ne pas converger du tout si le point de départ de l'algorithme est trop loin du minimum ou si la matrice ${\displaystyle \mathbf {J_{r}^{T}J_{r}} }$ est mal conditionnée.

L'algorithme peut donc échouer à converger. Par exemple, le problème avec ${\displaystyle m=2}$ équations et ${\displaystyle n=1}$ variable, donné par

${\displaystyle {\begin{aligned}r_{1}(\beta )&=\beta +1\\r_{2}(\beta )&=\lambda \beta ^{2}+\beta -1.\end{aligned}}}$

L'optimum se situe en ${\displaystyle \beta =0}$. Si ${\displaystyle \lambda =0}$ alors le problème est en fait linéaire et la méthode trouve la solution en une seule itération. Si |λ| < 1, alors la méthode converge linéairement et les erreurs décroissent avec un facteur |λ| à chaque itération. Cependant, si |λ| > 1, alors la méthode ne converge même pas localement[5].

Dans ce qui suit, l'algorithme de Gauss–Newton sera tiré de l'algorithme d'optimisation de Newton; par conséquent, la vitesse de convergence sera au plus quadratique.

La relation de récurrence de la méthode de Newton pour minimiser une fonction S de paramètres ${\displaystyle {\boldsymbol {\beta }}}$, est

${\displaystyle {\boldsymbol {\beta }}^{s+1}={\boldsymbol {\beta }}^{s}-\mathbf {H} ^{-1}\mathbf {g} \,}$

où g représente le gradient de S et H sa matrice hessienne.

Puisque ${\displaystyle S=\sum _{i=1}^{m}r_{i}^{2}}$, la j-ème composante du gradient de S est :

${\displaystyle g_{j}=2\sum _{i=1}^{m}r_{i}{\frac {\partial r_{i}}{\partial \beta _{j}}}.}$

Les éléments de la Hessienne sont calculés en dérivant les éléments du gradient, ${\displaystyle g_{j}}$, par rapport à ${\displaystyle \beta _{k}}$

${\displaystyle H_{jk}=2\sum _{i=1}^{m}\left({\frac {\partial r_{i}}{\partial \beta _{j}}}{\frac {\partial r_{i}}{\partial \beta _{k}}}+r_{i}{\frac {\partial ^{2}r_{i}}{\partial \beta _{j}\partial \beta _{k}}}\right).}$

La méthode de Gauss–Newton est obtenue en ignorant les dérivées d'ordre supérieur ou égal à deux. La Hessienne est approchée par

${\displaystyle H_{jk}\approx 2\sum _{i=1}^{m}J_{ij}J_{ik}}$

où ${\displaystyle J_{ij}={\frac {\partial r_{i}}{\partial \beta _{j}}}}$ est l'élément ${\displaystyle (i,j)}$ de la jacobienne ${\displaystyle \mathbf {J_{r}} }$. Le gradient et la hessienne approchée sont alors

${\displaystyle \mathbf {g} =2\mathbf {J_{r}^{T}r,\quad H\approx 2J_{r}^{T}J_{r}} .\,}$

Ces expressions sont remplacées dans la relation de récurrence initiale afin d'obtenir la relation récursive :

${\displaystyle {\boldsymbol {\beta }}^{s+1}={\boldsymbol {\beta }}^{s}+\delta {\boldsymbol {\beta }};\ \delta {\boldsymbol {\beta }}=-\mathbf {\left(J_{r}^{T}J_{r}\right)^{-1}J_{r}^{T}r} .}$

La convergence de la méthode n'est pas toujours garantie. L'approximation

${\displaystyle \left|r_{i}{\frac {\partial ^{2}r_{i}}{\partial \beta _{j}\partial \beta _{k}}}\right|\ll \left|{\frac {\partial r_{i}}{\partial \beta _{j}}}{\frac {\partial r_{i}}{\partial \beta _{k}}}\right|}$

doit être vraie pour pouvoir ignorer les dérivées du second ordre. Cette approximation peut être valide dans les deux cas suivants, pour lesquels on peut s'attendre à obtenir la convergence[6] :

1. les valeurs de la fonction ${\displaystyle r_{i}}$ sont petites en magnitude, au moins près du minimum ;
2. les fonctions sont seulement faiblement non linéaires, si bien que ${\displaystyle {\frac {\partial ^{2}r_{i}}{\partial \beta _{j}\partial \beta _{k}}}}$ est relativement petit en magnitude.

Avec la méthode de Gauss–Newton, la somme des carrés S peut ne pas décroître à chaque itération. Toutefois, (puisque) si ${\displaystyle \delta {\boldsymbol {\beta }}}$ est une direction de descente, à moins que ${\displaystyle {\boldsymbol {\beta }}^{s}}$ soit un point stationnaire, il se trouve que pour tout ${\displaystyle \alpha >0}$ suffisamment petit,

${\displaystyle S({\boldsymbol {\beta }}^{s}+\alpha \ \delta {\boldsymbol {\beta }})<S({\boldsymbol {\beta }}^{s})}$

Ainsi, en cas de divergence, une solution est d'employer un facteur ${\displaystyle \alpha }$ d'amortissement de l'incrément ${\displaystyle \delta {\boldsymbol {\beta }}}$ dans la formule de mise à jour :

${\displaystyle {\boldsymbol {\beta }}^{s+1}={\boldsymbol {\beta }}^{s}+\alpha \ \delta {\boldsymbol {\beta }}}$

En d'autres termes, le vecteur d'incrément est trop long, mais pointe bien vers le bas, si bien que parcourir une fraction du chemin fait décroître la fonction objectif S. Une valeur optimale pour ${\displaystyle \alpha }$ peut être trouvée en utilisant un algorithme de recherche linéaire : la magnitude de ${\displaystyle \alpha }$ est déterminée en trouvant le minimum de S en faisant varier α sur une grille de l'intervalle ${\displaystyle 0<\alpha <1}$. On peut aussi réévaluer α de manière simple à chaque étape, par exemple par dichotomie :

• en le diminuant (par exemple en lui appliquant un facteur 0,5) jusqu'à ce que l'on ait S(β^s + αδβ^s) < S(β^s) ;
• en l'augmentant pour la fois suivante lorsque la condition est remplie (par exemple en le rapprochant de 1 en prenant (1 + α)/2).

Cet démarche n'est pas optimale, mais réduit l'effort nécessaire à déterminer α.

Dans le cas où la direction de l'incrément est telle que α est proche de zéro, une méthode alternative pour éviter la divergence est l'algorithme de Levenberg-Marquardt. Les équations normales sont modifiées de telle sorte que l'incrément est décalé en direction de la descente la plus forte

${\displaystyle \left(\mathbf {J^{T}J+\lambda D} \right)\delta {\boldsymbol {\beta }}=\mathbf {J} ^{T}\mathbf {r} }$,

où D est une matrice diagonale positive. Remarquons que lorsque D est la matrice identité et que ${\displaystyle \lambda \to +\infty }$, alors ${\displaystyle \lambda \delta {\boldsymbol {\beta }}\to \mathbf {J} ^{T}\mathbf {r} }$, par conséquent la direction de ${\displaystyle \delta {\boldsymbol {\beta }}}$ s'approche de la direction du gradient positivement lié à ${\displaystyle \mathbf {J} ^{T}\mathbf {r} }$.

Le paramètre de Marquardt, ${\displaystyle \lambda }$, peut aussi être optimisé par une méthode de recherche linéaire, mais ceci rend la méthode fort inefficace dans la mesure où le vecteur d'incrément ${\displaystyle \delta {\boldsymbol {\beta }}}$ doit être re-calculé à chaque fois que ${\displaystyle \lambda }$ change.

Dans une méthode quasi-Newton, comme celle due à Davidon, Fletcher et Powell, une estimation de la matrice Hessienne, ${\displaystyle {\frac {\partial ^{2}S}{\partial \beta _{j}\partial \beta _{k}}}}$, est approchée numériquement en utilisant les premières dérivées ${\displaystyle {\frac {\partial r_{i}}{\partial \beta _{j}}}}$.

Une autre méthode pour résoudre les problèmes de moindres carrés en utilisant seulement les dérivées premières est l'algorithme du gradient. Toutefois, cette méthode ne prend pas en compte les dérivées secondes, même sommairement. Par conséquent, cette méthode s'avère particulièrement inefficace pour beaucoup de fonctions.

• Régression non linéaire
• Ajustement de courbe
• Algorithme de Levenberg-Marquardt

• Calcul d'incertitudes Un livre de 246 pages qui étudie la régression linéaire et non-linéaire. L'algorithme est détaillé et appliqué à l'expérience de biologie traitée en exemple dans cet article (page 79 avec les incertitudes sur les valeurs estimées).

• Portail de l'informatique théorique
• Portail des mathématiques