Graphe de Hoffman-Singleton
Le graphe de Hoffman-Singleton est, en théorie des graphes, un graphe possédant 50 sommets et 175 arêtes[1]. C'est Alan Hoffman et Robert Singleton qui le découvrirent en essayant de classifier les graphes de Moore[2].
| Graphe de Hoffman-Singleton | |
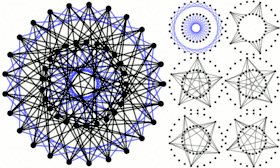 Schéma du graphe de Hoffman-Singleton, présentant ses 50 sommets sous la forme de deux cercles concentriques de 25 sommets. | |
| Nombre de sommets | 50 |
|---|---|
| Nombre d'arêtes | 175 |
| Distribution des degrés | 7-régulier |
| Rayon | 2 |
| Diamètre | 2 |
| Maille | 5 |
| Automorphismes | 252 000 |
| Nombre chromatique | 4 |
| Indice chromatique | 7 |
| Propriétés | Cage Fortement régulier Graphe de Moore Hamiltonien Intégral Symétrique |
Construction
Il est possible de construire le graphe de Hoffman-Singleton à partir de pentagones et de pentagrammes. Considérons C5 le graphe cycle à cinq sommets, représenté comme une pentagone, et P5, le même graphe représenté comme une pentagramme. Prenons cinq copies de C5, notés C1 à C5 et cinq copies de P5 notés P1 à P5. Pour tout triplet (i, j,h), relions le sommet numéro j de Ch au sommet numéro hi+j modulo 5 de Pi. Le graphe obtenu a 5 × 5 + 5 × 5 = 50 sommets et 175 arêtes.
Le graphe de Hoffman-Singleton peut aussi être vu comme un sous-graphe du graphe de Higman-Sims.
Propriétés
Propriétés générales
Le graphe de Hoffman-Singleton est une (7,5)-cage, c'est-à-dire un graphe minimal en nombres de sommets ayant une maille de 5 et étant un graphe régulier de degré 7. Il s'agit de l'unique (3,7)-cage et sa taille coïncide avec la borne de Moore, une borne inférieure sur le nombre de sommets que peut avoir une cage. Un tel graphe est qualifié de graphe de Moore.
Le diamètre du graphe de Hoffman-Singleton, l'excentricité maximale de ses sommets, ainsi que son rayon, l'excentricité minimale de ses sommets, sont tous deux égaux à 2. Cela entraine que tous ses sommets appartiennent à son centre.
Le graphe de Hoffman-Singleton est 7-sommet-connexe et 7-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 7 sommets ou de 7 arêtes. Comme il est régulier de degré 7 ce nombre est optimal. Le graphe de Hoffman-Singleton est donc un graphe optimalement connecté.
Il est également hamiltonien, c'est-à-dire qu'il possède un cycle passant par tous les sommets une et une seule fois. .
Coloration
Le nombre chromatique du graphe de Hoffman-Singleton est 4. C'est-à-dire qu'il est possible de le colorer avec 4 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal[3].
L'indice chromatique du graphe de Hoffman-Singleton est 7. Il existe donc une 7-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal[4].
Propriétés algébriques
Le groupe d'automorphismes du graphe de Hoffman-Singleton est d'ordre 252 000. Il agit transitivement sur les sommets, les arêtes et les arcs. Le graphe d'Hoffman-Singleton est donc un graphe symétrique[5].
Le polynôme caractéristique de la matrice d'adjacence du graphe de Hoffman-Singleton est : . Ce polynôme caractéristique n'admet que des racines entières. Le graphe de Hoffman-Singleton est donc un graphe intégral, un graphe dont le spectre est constitué d'entiers. C'est aussi le seul graphe avec ce polynôme caractéristique ce qui fait de lui un graphe déterminé de façon unique par son spectre, c'est-à-dire l'ensemble des valeurs propres de sa matrice d'adjacence.
Références
- (en) Eric W. Weisstein, « Hoffman-Singleton Graph », sur MathWorld
- (en) Alan J. Hoffman et Robert R. Singleton, « Moore graphs with diameter 2 and 3 », IBM Journal of Research and Development, vol. 5, no 4, , p. 497–504 (DOI 10.1147/rd.45.0497)
- (en) Hoffman-Singleton graph sur la page d'Andries E. Brouwer, de l'université technique d'Eindhoven
- (en) Re: What is the Edge Chromatic Number of Hoffman-Singleton?, réponse de Gordon Royle en 2004, sur le forum GRAPHNET@istserv.nodak.edu
- (en) Paul R. Hafner, « The Hoffman-Singleton Graph and Its Automorphisms », Journal of Algebraic Combinatorics, vol. 18, no 1, , p. 7-12 (DOI 10.1023/A:1025136524481, lire en ligne [ps])