Graphe dual
En théorie des graphes, le graphe dual d'un graphe plongé dans une surface est défini à l'aide des composantes de son complémentaire, lesquelles sont reliées entre elles par les arêtes du graphe de départ.
Pour les articles homonymes, voir Dualité (mathématiques) pour les autres notions de dualité en mathématiques.
Cette notion généralise celle de dualité dans les polyèdres.
Il faut noter qu'un même graphe abstrait peut avoir des graphes duaux non isomorphes en fonction du plongement choisi, même dans le cas de plongements dans le plan.
Un graphe (plongé) isomorphe à son dual est dit autodual.
Construction
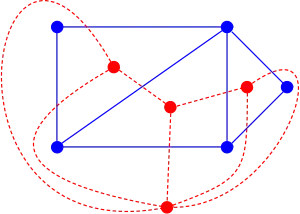
Étant donné un graphe plongé dans une surface connexe, chaque composante connexe (ou cellule) du complémentaire est munie d'un point définissant un sommet du graphe dual. Chaque arête du graphe initial définit une arête du graphe dual reliant les composantes du complémentaire qui la bordent[1]. Les arêtes du graphe dual peuvent être plongées dans la surface de façon que chacune coupe uniquement l'arête correspondante du graphe initial, et en un seul point.
Propriétés
- Un graphe dual est toujours connexe.
- Un graphe connexe plongé dans le plan est le dual de son graphe dual (à homotopie près du plongement).
- Le graphe dual d'un graphe planaire est planaire également par construction.
- Un graphe dual peut comporter des boucles et des arêtes multiples même si le graphe initial est planaire et simple.
Unicité
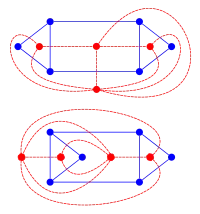
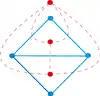
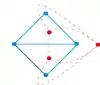
Le dual est défini pour un plongement donné, et deux plongements donnés d'un même graphe peuvent donner naissance à des duaux non isomorphes. Dans la figure ci-contre par exemple, le premier dual a un sommet de degré 6 (car la face externe est bordée par 6 arêtes) tandis que le deuxième a des sommets de degré 5 au maximum.
Par contre, la somme des degrés des sommets du dual sera toujours la même, égale au double du nombre d'arêtes du graphe de départ.
De plus, un même plongement peut donner naissances à deux graphes duaux qui sont certes combinatoirement isomorphes, mais non topologiquement équivalents, dans le plan (ils le seraient dans la sphère).
Exemples
- Le graphe tétraédrique plongé sur le plan est son propre dual (on dit d'un tel graphe qu'il est autodual).