Graphe (mathématiques discrètes)

En mathématiques, et plus précisément en théorie des graphes, un graphe est une structure composée d'objets dans laquelle certaines paires d'objets sont en relation. Les objets correspondent à des abstractions mathématiques et sont appelés sommets (ou nœuds ou points), et les relations entre sommets sont des arêtes (ou liens ou lignes)[1]. On distingue les graphes non orientés, où les arêtes relient deux sommets de manière symétrique, et les graphes orientés, où les arêtes, alors appelées flèches, relient deux sommets de manière asymétrique.

Un graphe avec six sommets et sept arêtes.

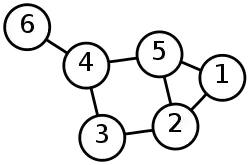
Un graphe est fréquemment représenté par un diagramme sous la forme d'un ensemble de points pour les sommets, joints entre eux par des lignes droites ou courbes pour les arêtes, éventuellement munies de flèches pour le cas de graphes orientés. Les graphes sont l'un des objets d'étude du champ des mathématiques discrètes.

Les graphes constituent l'objet de base de la théorie des graphes. Le mot « graph » a été utilisé pour la première fois dans ce sens par James Joseph Sylvester en 1878[2]^,[3].

Définitions

Il existe plusieurs variantes dans la définition des graphes en théorie des graphes. Les définitions les plus usuelles sont les suivantes.

Graphe

Un graphe avec trois sommets et trois arêtes.

Dans un sens restreint mais très répandu du terme[4]^,[5], un graphe est un couple G = (V, E) comprenant

V un ensemble de sommets (aussi appelés nœuds ou points) ;
E ⊆ {{x, y} | (x, y) ∈ V² ∧ x ≠ y} un ensemble d'arêtes (aussi appelées liens, ou lignes), qui sont des paires de sommets (c.-à-d. qu'une arête est associée à deux sommets distincts).

Pour lever toute ambiguïté, ce type d'objet peut être appelé précisément un graphe simple non orienté.

Dans l'arête {x, y}, les sommets x et y sont appelés les extrémités ou les sommets extrêmes de l'arête. On dit que l'arête joint x et y et est incidente sur x et sur y. Un sommet peut exister dans un graphe sans arête incidente. Une boucle est une arête qui joint un sommet à lui-même. Les arêtes multiples sont deux arêtes ou plus qui joignent les mêmes deux sommets.

Dans un sens plus général du terme autorisant les arêtes multiples[6]^,[7], un graphe est un triplet G = (V, E, ϕ) comprenant

V un ensemble de sommets (aussi appelés nœuds ou points) ;
E un ensemble d'arêtes (aussi appelés liens ou lignes) ;
ϕ: E → {{x, y} | (x, y) ∈ V² ∧ x ≠ y} une fonction d'incidence associant à chaque arête une paire de sommets (c.-à-d. qu'une arête est associée à deux sommets distincts).

Pour lever toute ambiguïté, ce type d'objet peut être appelé précisément un multigraphe non orienté.

Les graphes tels que définis dans les deux définitions précédentes ne peuvent pas avoir de boucles, car une boucle joignant un sommet x est l'arête (pour un graphe simple non orienté) ou est incidente sur (pour un multigraphe non orienté) {x, x} = {x} qui n'est pas dans {{x, y} | (x, y) ∈ V² ∧ x ≠ y}. Ainsi pour autoriser les boucles les définitions doivent être étendues. Pour les graphes simples non orientés, E ⊆ {{x, y} | (x, y) ∈ V² ∧ x ≠ y} doit devenir E ⊆ {{x, y} | (x, y) ∈ V²}. Pour les multigraphes non orientés, ϕ: E → {{x, y} | (x, y) ∈ V² ∧ x ≠ y} doit devenir ϕ: E → {{x, y} | (x, y) ∈ V²}. Pour lever toute ambiguïté, ces types d'objets peuvent être appelés précisément un graphe simple non orienté avec boucles et un multigraphe non orienté avec boucles respectivement.

V et E sont en général supposés finis, et de nombreux résultats cessent d'être vrais (ou ont des énoncés différents) pour des graphes infinis parce que certains arguments de preuve ne se transposent pas au cas infini. De plus, V est souvent supposé non vide, mais E peut être l'ensemble vide.

L'ordre d'un graphe |V| est son nombre de sommets. La taille d'un graphe est |E|, son nombre d'arêtes. Le degré ou la valence d'un sommet est le nombre d'arêtes incidentes à ce sommet, où une boucle compte double.

Dans un graphe simple non orienté d'ordre n, le degré maximum d'un sommet est n − 1 et la taille maximale du graphe est n(n − 1)/2.

Les arêtes E d'un graphe non orienté G induisent une relation binaire symétrique ~ sur V appelée le relation d'adjacence de G. Spécifiquement, pour chaque arête {x, y}, ses sommets extrêmes x et y sont dits adjacents l'un l'autre, ce qui est noté x ~ y.

Graphe orienté

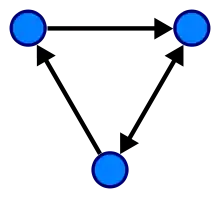
Un graphe orienté avec trois sommets et quatre arêtes.

Un graphe orienté est un graphe dans lequel les arêtes possèdent une orientation.

Dans un sens restreint mais très répandu du terme[8], un graphe orienté est un couple G = (V, A) (parfois G = (V, E)) comprenant

V un ensemble de sommets (aussi appelés nœuds ou points) ;
A ⊆ {(x, y) | (x, y) ∈ V² ∧ x ≠ y} un ensemble de flèches (aussi appelées arêtes orientées — parfois simplement arêtes avec l'ensemble correspondant nommé E au lieu de A —, liens orientés ou lignes orientées), qui sont des couples de sommets distincts (c.-à-d. une flèche est associée à deux sommets distincts).

Pour lever toute ambiguïté, ce type d'objet peut être appelé précisément un graphe simple orienté.

Dans la flèche (x, y) orientée de x vers y, x est appelé la queue de la flèche et y la tête de la flèche. La flèche (y, x) est appelée la flèche inverse de (x, y).

Dans un sens plus général du terme autorisant les flèches multiples[6]^,[7], un graphe orienté est un triplet G = (V, A, ϕ) (parfois G = (V, E, ϕ)) comprenant

V un ensemble de sommets (aussi appelés nœuds ou points) ;
A un ensemble de flèches (aussi appelées arêtes orientées — parfois simplement arêtes avec l'ensemble correspondant nommé E au lieu de A —, liens orientés ou lignes orientées);
ϕ: A → {(x, y) | (x, y) ∈ V² ∧ x ≠ y} une fonction d'incidence associant à chaque flèche un couple de sommets distincts (c.-à-d. une flèche est associée à deux sommets distincts).

Pour lever toute ambiguïté, ce type d'objet peut être appelé précisément un multigraphe orienté.

Les graphes orientés tels que définis dans les deux définitions précédentes ne peuvent pas avoir de boucles, car une boucle joignant un sommet x est la flèche (pour un graphe simple orienté) ou est incidente sur (pour un multigraphe orienté) (x, x) qui n'est pas dans {(x, y) | (x, y) ∈ V² ∧ x ≠ y}. Ainsi pour autoriser les boucles les définitions doivent être étendues. Pour les graphes simples orientés, A ⊆ {(x, y) | (x, y) ∈ V² ∧ x ≠ y} doit devenir A ⊆ V². Pour les multigraphes orientés, ϕ: A → {(x, y) | (x, y) ∈ V² ∧ x ≠ y} doit devenir ϕ: A → V². Pour lever toute ambiguïté, ces types d'objets peuvent être appelés précisément un graphe simple orienté avec boucles et un multigraphe orienté avec boucles (ou un carquois) respectivement.

Un graphe simple orienté avec boucles est une relation homogène (une relation binaire entre un ensemble et lui-même). Un graphe simple orienté avec boucles G = (V, A) est dit symétrique si, pour chaque flèche de A, la flèche inverse correspondante appartient aussi à A.

Graphe mixte

Un graphe mixte est un graphe composé d'arêtes non orientées et d'arêtes orientées. C'est un triplet G = (V, E, A) pour un graphe mixte simple et G = (V, E, A, ϕ_E, ϕ_A) pour un multigraphe mixte avec V, E, A, ϕ_E et ϕ_A définis comme précédemment. Les graphes orientés et non orientés en sont des cas particuliers.

Graphe pondéré

Un graphe pondéré avec dix sommets et douze arêtes.

Un graphe pondéré ou un réseau[9] est un graphe où chaque arête porte un nombre (son poids)[10]. Ces poids peuvent représenter par exemple des coûts, des longueurs ou des capacités, en fonction du problème traité. Ces graphes sont fréquents dans divers contextes, comme le problème de plus court chemin ou le problème du voyageur de commerce.

Types de graphes

Graphe asymétrique

Un graphe asymétrique (en anglais « oriented graph ») est un graphe orienté où l'un au plus des couples (x, y) et (y, x) est une flèche du graphe. Un tel graphe est sans boucle. On peut le voir comme résultant du choix d'une orientation pour chaque arête d'un graphe non orienté sans boucle.

Graphe régulier

Un graphe régulier est un graphe (non orienté) où tous les sommets ont même degré. Si ce degré est k, on parle aussi de graphe k-régulier.

Graphe complet

Le graphe complet à 7 sommets.

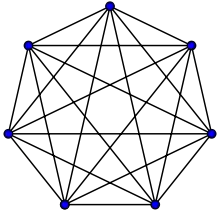
Un graphe complet est un graphe simple dont les sommets sont tous adjacents les uns aux autres, c'est-à-dire tel que tout couple de sommets distincts est relié par une arête. Si le graphe est orienté, on dit qu'il est complet si chaque paire de sommets est reliée par exactement deux flèches (une dans chaque sens).

Graphe fini

Un graphe fini est un graphe dont l'ensemble de sommets est fini (et donc aussi l'ensemble d'arêtes). Dans le cas contraire, c'est un graphe infini. Le plus souvent, les graphes considérés sont tacitement supposés finis ; s'ils sont infinis, ceci est spécifié explicitement.

Graphe connexe

Un graphe connexe est un graphe non orienté où toute paire de sommets est reliée par une chaîne. Un graphe orienté, est connexe si le graphe non orienté obtenu en oubliant les orientations des arêtes est connexe. Il est fortement connexe si tout couple de sommets est relié par un chemin, donc si pour tout couple (x, y) de sommets, il y a un chemin de x à y et un chemin de y à x. Un graphe k-sommet-connexe est un graphe qui possède au moins k+1 sommets et qui reste encore connexe après en avoir ôté k–1 ; de même, un graphe k-arête-connexe est un graphe qui reste connexe quand on lui enlève k–1 arêtes.

Graphe biparti

Un graphe biparti complet.

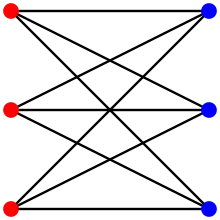
Un graphe biparti est un graphe dont l'ensemble des sommets peut être partitionné en deux ensembles X et Y de telle sorte qu'il n'y a pas d'arête entre deux sommets de X ni entre deux sommets de Y. De manière équivalente, un graphe biparti est un graphe dont le nombre chromatique est 2.

Un graphe biparti complet est un graphe biparti où tous les sommets de X sont reliés à tous les sommets de Y et vice-versa.

Chaîne

Un graphe est une chaîne d'ordre n ≥ 2 s'il est composé de sommets n qu'on peut numéroter de telle sorte que les arêtes sont {v_i, v_i+1} pour i = 1, 2, …, n − 1. Une chaîne est, de manière équivalente, un graphe connexe dont tous les sommets sont de degré 2 sauf deux qui sont de degré 1. Une chaîne dans un graphe est un sous-graphe partiel de ce graphe.

Graphe planaire

Un graphe planaire est un graphe que l'on peut dessiner dans le plan (ou sur une sphère) sans que deux arêtes ne se croisent.

Graphe cycle

Un graphe cycle d'ordre $n\geq 3$ ou n-cycle est un graphe dont les sommets peuvent être numérotés $v_{1},\ldots ,v_{n}$ de sorte que les arêtes sont les paires $[v_{i},v_{i+1}]$ pour $i=1,\ldots ,n-1$ plus l'arête $[v_{n},v_{1}]$ . Un graphe cycle peut être caractérisé comme étant un graphe connexe dont tous les sommets ont degré 2.

Arbre

Un arbre est un graphe connexe acyclique.

Une forêt est un graphe acyclique, c'est-à-dire une union disjointe d'un ou plusieurs arbres.

Autres classes

D'autres classes de graphes comprennent:

Graphe de Petersen et ses généralisations;
Graphes parfaits;
Cographes;
Graphes cordaux;
d'autres graphes classées en fonction de leur groupe d'automorphisme : graphe sommet-transitif, graphe symétrique, et graphe distance-transitif ;
Graphe fortement régulier et leurs généralisations ; graphe distance-régulier.

Propriétés de graphes

Deux arêtes d'un graphe sont adjacentes si elles ont un sommet en commun. Deux arcs d'un graphe orienté sont consécutifs si la fin du premier arc est le début du deuxième. De même, deux sommets sont adjacents s'il sont extrémités d'une même arête (d'un même arc). Une arête et un sommet adjacent sont dits incidents l'un à l'autre.

Le graphe formé d'un seul sommet et sans arêtes est souvent appelé trivial ; le graphe sans sommet ni arête est aussi appelé parfois le graphe nul.

Un graphe est étiqueté aux sommets si chaque sommet porte une étiquette. Un graphe est étiqueté aux arêtes si chaque arête porte une étiquette. On peut considérer, dans les problèmes d'énumération ou de bijection, des graphes étiquetés ou non étiquetés. Un graphe dont les sommets (ou les arêtes) sont étiquetés par des couleurs est un graphe coloré.

Propriétés de centralités d'un graphe

Dans l'analyse de graphes, la centralité mesure la pertinence et l'importance d'un sommet. On distingue :

la centralité de degré qui est le nombre d'arêtes incidentes à un sommet ;
la centralité de proximité qui est l'inverse de la somme des distances à tous les autres sommets ;
la centralité d'intermédiarité qui est le nombre total de chemins les plus courts passant par un sommet[11].

D'autres mesures sont l'excentricité d'un sommet qui est la distance maximale à tout autre sommet, le diamètre d’un graphe ou le rayon .

Opérations sur les graphes

Les diverses opérations qui produisent de nouveaux graphes à partir de graphes donnés peuvent être regroupées en :

opérations unaires, qui créent un nouveau graphe à partir d'un ancien, comme :
opérations binaires, qui créent un nouveau graphe à partir de deux anciens, comme :
- union disjointe de graphes,
- produit cartésien,
- produit tensoriel,
- produit fort,
- produit lexicographique,
- graphe série-parallèle.

Applications

Le graphe de Cayley du groupe libre sur a et b.

Molécule de saccharine.

En théorie des catégories, une catégorie peut être représentée par un multigraphe orienté dont les sommets représentent les objets et les arêtes les morphismes. Un foncteur entre catégories induit un morphisme de graphes.
En informatique, les graphes orientés sont utilisés pour représenter des notions comme les graphes conceptuels, les automates finis et de nombreux autres structures discrètes. Il est également possible de modéliser le fonctionnement d'un réseau neuronal artificiel, ou encore le schéma décisionnel d'une intelligence artificielle.
Une relation binaire R sur un ensemble X définit un graphe orienté (et réciproquement). Il y a une flèche de x à y dans le graphe si et seulement si xRy.
Un graphe peut modéliser des informations sur des réseaux sociaux, comme la notion de « follower » dans Twitter[12]^,[13].
Des exemples de graphes orientés réguliers sont les graphes de Cayley de groupes finiment engendrés, ou le graphe des cosets de Schreier (en).
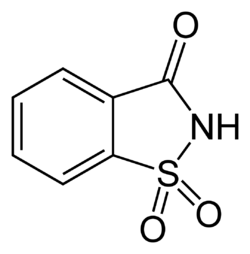
En chimie et notamment dans la représentation simplifiée des liaisons entre atomes formant une molécule, des graphes en général non orientés mais avec des arêtes multiples sont largement utilisés.

Extensions

Les graphes se généralisent dans plusieurs directions :

Dans un hypergraphe, une arête peut relier plus de deux sommets.
Un graphe non orienté peut être vu comme un complexe simplicial dont les 1-Simplexes sont les arêtes et les 0-simplexes les sommets. Sous cet aspect, les complexes simpliciaux sont des généralisation des graphes à des dimensions plus élevées.
Tout graphe donne aussi un matroïde.
En théorie des modèles, un graphe est juste une structure logique. Dans ce cadre, il n'y a pas de limitation aux nombre d'arêtes qui peut être tout nombre cardinal.
En bio-informatique, l'analyse en graphe de puissance introduit de graphes particuliers (les « power graphs ») comme une alternative pour la représentation de graphes non orientés.
Dans les systèmes d'information géographique, les réseaux géométriques sont des modèles proches des graphes, et empruntent à la théorie des graphes de nombreux concepts pour l'analyse spatiales sur les réseaux routiers ou des repères d'utilisation.

Notes et références

Trudeau 1993, p. 19 : « A graph is an object consisting of two sets called its vertex set and its edge set ».
Dans :J. J. Sylvester, « Chemistry and algebra », Nature, vol. 17,‎ 7 février 1878, p. 284 : "Every invariant and covariant thus becomes expressible by a graph precisely identical with a Kekuléan diagram or chemicograph." (DOI 10.1038/017284a0, lire en ligne). et J. J. Sylvester, « On an application of the new atomic theory to the graphical representation of the invariants and covariants of binary quantics, — with three appendices », American Journal of Mathematics, Pure and Applied’, vol. 1, n^o 1,‎ 1878, p. 64–90 (DOI 10.2307/2369436, lire en ligne).
Gross et Yellen 2004, p.35.
(en) Edward A. Bender et S. Gill Williamson, Lists, Decisions and Graphs : With an Introduction to Probability, 2010, 251 p. (lire en ligne), p. 148
Par exemple (Iyanaga et Kawada 1977, p. 234) ou (Biggs 1993, p. 4).
(en) Edward A. Bender et S. Gill Williamson, Lists, Decisions and Graphs : With an Introduction to Probability, 2010, 251 p. (lire en ligne), p. 149
Par exemple (Graham et. al. 1995, p. 5).
(en) Edward A. Bender et S. Gill Williamson, Lists, Decisions and Graphs : With an Introduction to Probability, 2010, 251 p. (lire en ligne), p. 161
Strang 2005.
Fletcher, Hoyle et Patty 1991, p. 463 : A weighted graph is a graph in which a number w(e), called its weight, is assigned to each edge e.
Xingqin Qi, Eddie Fuller, Qin Wu et Yezhou Wu, « Laplacian centrality: A new centrality measure for weighted networks », Information Sciences, vol. 194,‎ juillet 2012, p. 240–253 (ISSN 0020-0255, DOI 10.1016/j.ins.2011.12.027).
Martin Grandjean, « A social network analysis of Twitter: Mapping the digital humanities community », Cogent Arts & Humanities, vol. 3, n^o 1,‎ 2016, p. 1171458 (DOI 10.1080/23311983.2016.1171458, lire en ligne)
Pankaj Gupta, Ashish Goel, Jimmy Lin, Aneesh Sharma, Dong Wang, and Reza Bosagh Zadeh WTF: The who-to-follow system at Twitter, Proceedings of the 22nd international conference on World Wide Web. DOI:10.1145/2488388.2488433.

Annexes

Bibliographie

Ouvrages généraux

Tous les manuels de mathématiques discrètes contiennent un traitement des graphes :

Peter Fletcher, Hughes Hoyle et C. Wayne Patty, Foundations of Discrete Mathematics, Boston, PWS-KENT Pub. Co., 1991, 781 p. (ISBN 0-534-92373-9)
Ronald L. Graham, Martin Grötschel et Lovász Lovász (direction), Handbook of Combinatorics, MIT Press, 1995 (ISBN 0-262-07169-X)
Shôkichi Iyanaga et Yukiyosi Kawada, Encyclopedic Dictionary of Mathematics, MIT Press, 1977 (ISBN 0-262-09016-3)
Gilbert Strang, Linear Algebra and Its Applications, Brooks Cole, 2005, 4^e éd., 487 p. (ISBN 0-03-010567-6, lire en ligne).
(en) Daniel Zwillinger, CRC Standard Mathematical Tables and Formulae, Boca Raton/London/New York etc., Chapman & Hall/CRC, 27 novembre 2002, 31^e éd., 910 p. (ISBN 1-58488-291-3)

Ouvrages spécifiques

De nombreux livres sont centrés sur la théorie des graphes :

R. Balakrishnan et K. Ranganathan, A Textbook of Graph Theory, New York, Springer-Verlag, coll. « Universitext », 2012, xiii+292 (ISBN 978-1-4614-4528-9, DOI 10.1007/978-1-4614-4529-6, lire en ligne)
Claude Berge, Théorie des graphes et ses applications, Paris, Collection Universitaire de Mathématiques, 1963, 2^e éd., viii+267 (SUDOC 007608756)
(en) Norman Biggs, Algebraic Graph Theory, Cambridge, Cambridge University Press, 1993, 2^e éd., 205 p. (ISBN 0-521-45897-8)
(en) Béla Bollobás, Modern Graph Theory, New York/Berlin/Paris, Springer, 12 août 2002, 1^re éd., 394 p. (ISBN 0-387-98488-7)
Jørgen Bang-Jensen et Gregory Z. Gutin, Digraphs : Theory, Algorithms and Applications, Springer-Verlag, 2000 (lire en ligne)
Reinhard Diestel, Graph Theory, Springer, coll. « Graduate Texts in Mathematics » (n^o 173), août 2016 (réimpr. 2010, 2005, 2000, 1997), 5^e éd., 447 p. (ISBN 978-3-662-53621-6 et 978-3-96134-005-7, présentation en ligne, lire en ligne)
(en) Jonathan L. Gross et Jay Yellen, Graph Theory and Its Applications, Boca Raton (Fla.)/London/New York etc., CRC Press, 30 décembre 1998, 585 p. (ISBN 0-8493-3982-0, lire en ligne)
Jonathan L. Gross et Jay Yellen (éditeurs), Handbook of graph theory, CRC Press, 2004, 1192 p. (ISBN 978-1-58488-090-5, lire en ligne).
Frank Harary, Graph Theory, Addison Wesley Publishing Company, janvier 1995 (ISBN 0-201-41033-8)
Richard J. Trudeau, Introduction to Graph Theory, New York, Dover Publications, 1993, 209 p. (ISBN 978-0-486-67870-2, présentation en ligne)

Articles connexes

Liens externes

(en) Eric W. Weisstein, « Graph », sur MathWorld
Notice dans un dictionnaire ou une encyclopédie généraliste :
- Brockhaus Enzyklopädie

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Trudeau 1993, p. 19 : « A graph is an object consisting of two sets called its vertex set and its edge set ».

[2] Dans :J. J. Sylvester, « Chemistry and algebra », Nature, vol. 17,‎ 7 février 1878, p. 284 : "Every invariant and covariant thus becomes expressible by a graph precisely identical with a Kekuléan diagram or chemicograph." (DOI 10.1038/017284a0, lire en ligne). et J. J. Sylvester, « On an application of the new atomic theory to the graphical representation of the invariants and covariants of binary quantics, — with three appendices », American Journal of Mathematics, Pure and Applied’, vol. 1, n^o 1,‎ 1878, p. 64–90 (DOI 10.2307/2369436, lire en ligne).

[3] Gross et Yellen 2004, p.35.

[4] (en) Edward A. Bender et S. Gill Williamson, Lists, Decisions and Graphs : With an Introduction to Probability, 2010, 251 p. (lire en ligne), p. 148

[5] Par exemple (Iyanaga et Kawada 1977, p. 234) ou (Biggs 1993, p. 4).

[B&W-6] (en) Edward A. Bender et S. Gill Williamson, Lists, Decisions and Graphs : With an Introduction to Probability, 2010, 251 p. (lire en ligne), p. 149

[GGL_p5-7] Par exemple (Graham et. al. 1995, p. 5).

[8] (en) Edward A. Bender et S. Gill Williamson, Lists, Decisions and Graphs : With an Introduction to Probability, 2010, 251 p. (lire en ligne), p. 161

[9] Strang 2005.

[10] Fletcher, Hoyle et Patty 1991, p. 463 : A weighted graph is a graph in which a number w(e), called its weight, is assigned to each edge e.

[11] Xingqin Qi, Eddie Fuller, Qin Wu et Yezhou Wu, « Laplacian centrality: A new centrality measure for weighted networks », Information Sciences, vol. 194,‎ juillet 2012, p. 240–253 (ISSN 0020-0255, DOI 10.1016/j.ins.2011.12.027).

[snatwitter-12] Martin Grandjean, « A social network analysis of Twitter: Mapping the digital humanities community », Cogent Arts & Humanities, vol. 3, n^o 1,‎ 2016, p. 1171458 (DOI 10.1080/23311983.2016.1171458, lire en ligne)

[twitterwtf-13] Pankaj Gupta, Ashish Goel, Jimmy Lin, Aneesh Sharma, Dong Wang, and Reza Bosagh Zadeh WTF: The who-to-follow system at Twitter, Proceedings of the 22nd international conference on World Wide Web. DOI:10.1145/2488388.2488433.