Intégraphe
Un intégraphe est un appareil de la famille des intégrateurs, qui trace la courbe intégrale d'une fonction. Il fait partie de la famille des intégrateurs mécaniques, constituée d'instruments graphomécaniques tels que :
- les planimètres qui fournissent un résultat numérique (aire, moment statique ou moment d'inertie, etc.) en suivant le contour de la surface,
- les intégromètres qui fournissent ces valeurs, de manière continue, à mesure qu'ils suivent ce contour,
- les intégraphes qui permettent d'obtenir le tracé de la courbe intégrale correspondante.
Histoire
On attribue la première idée des planimètres, à l'ingénieur bavarois Johann Martin Hermann, de Munich, en 1814, appareil qui sera amélioré par Lämmle en 1816. L'appareil de l'Italien Tito Gonella de Florence, date de 1824, celui du Suisse Johannes Oppikofer de Berne, date de 1827. C'est le Suisse Alfred Amsler qui découvre, en 1879, le principe du planimètre polaire[1],[2].
En Grande-Bretagne, les premières traces explicites de l'utilisation et de la fabrication des planimètres, coïncident avec l'Exposition universelle de Londres, en 1851[3].
En France, l'idée première des intégraphes a été fournie dans une note, publiée en 1836, dans le Journal de mathématiques pures et appliquées, par le physicien Gustave Coriolis[4].
C'est l'ingénieur, mathématicien et inventeur polonais Bruno Abdank-Abakanowicz, qui réalisera les premiers intégraphes en 1878 et 1879. Avec son associé, David Napoli, Il imaginera en 1885, un modèle plus perfectionné avec des roues dentées (afin d'éliminer le glissement), et qui plus tard, sera commercialisé par le constructeur suisse Oswald & Gottlieb Coradi, à Zurich[5],[6].
Description
Voir catalogue Coradi (1900-1910 environ)[7],[8].
- Intégraphes Coradi
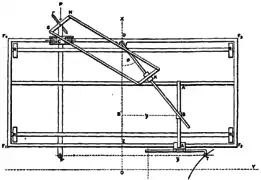 Plan intégraphe Coradi (1911) (Encyclopædia Britannica)
Plan intégraphe Coradi (1911) (Encyclopædia Britannica)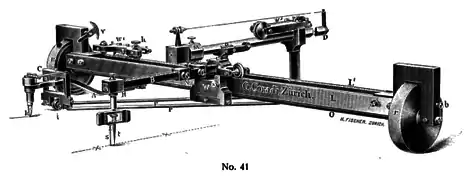 Intégraphe Bruno Abakanowicz, commercialisé par Coradi (catalogue 1915)
Intégraphe Bruno Abakanowicz, commercialisé par Coradi (catalogue 1915)
Utilisation
On place l'appareil sur la surface où se trouve la courbe de la fonction à traiter. On déplace un curseur le long de la courbe. L'appareil trace sur une feuille de papier la courbe intégrale de la courbe initiale.
Notes et références
Notes
Références
- Musée des arts et métiers, « Venez prendre l’aire ! Les instruments de mesure des surfaces » [PDF], sur irem.univ-reunion.fr (consulté en ).
- (de) Markus Coradi, « G. Coradi, Zürich 6, Mathematische Präzisionsinstrumente : Original-Katalog N°37 (voir planimètres polaires page 3, en français) », sur g.coradi.com (consulté le ).
- Rehseis, « Planimètres et intégraphes en Angleterre », sur irem.univ-reunion.fr (consulté le ).
- Gustave Coriolis - Journal de mathématiques pures et appliquées, « Note sur un moyen de tracer des courbes données par des équations différentielles (pages 5 à 9) », sur gallica.bnf.fr, (consulté le ).
- Rehseis, « Instruments graphomécaniques d'intégration (chapitre 5) », sur irem.univ-reunion.fr (consulté le ).
- (en) DrawingMachines, « Integraphs », sur drawingmachines.org (consulté le ).
- (en) IREM de la Réunion, « Integraph with transfer of direction by a linkage parallelogram, system Abdank-Abakanowicz/Coradi (large model) : Coradi integraph, system Abdank-Abakanowicz », sur irem.univ-reunion.fr (consulté le ).
- (de) Markus Coradi, « G. Coradi, Zürich 6, Mathematische Präzisionsinstrumente : Original-Katalog N°37 (voir intégraphes pages 12 et 13, en français) », sur g.coradi.com (consulté le ).
Articles connexes
Liens externes
- Portail des mathématiques
- Portail des technologies
- Portail de l’histoire