Iris de Fisher
Le jeu de données Iris connu aussi sous le nom de Iris de Fisher ou Iris d'Anderson est un jeu de données multivariées présenté en 1936 par Ronald Fisher dans son papier The use of multiple measurements in taxonomic problems comme un exemple d'application de l'analyse discriminante linéaire[1]. Les données ont été collectées par Edgar Anderson afin de quantifier les variations de morphologie des fleurs d'iris de trois espèces[2]. Deux des trois espèces ont été collectées en Gaspésie. « Toutes sont du même champ, cueillies le même jour et mesurées le même jour par la même personne avec les mêmes outils de mesures[3]. »
Pour les articles homonymes, voir Iris.
| Sujet principal | |
|---|---|
| Producteur | |
| Variables |
longueur des sépales en cm (Sepal length) , largeur des sépales en cm (Sepal width) , longueur des pétales en cm (Petal length), largeur des pétales en cm (Petal width), Espèce (Species) |
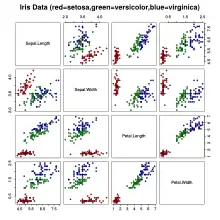
Le jeu de données comprend 50 échantillons de chacune des trois espèces d'iris (Iris setosa, Iris virginica et Iris versicolor). Quatre caractéristiques ont été mesurées à partir de chaque échantillon : la longueur et la largeur des sépales et des pétales, en centimètres. Sur la base de la combinaison de ces quatre variables, Fisher a élaboré un modèle d'analyse discriminante linéaire permettant de distinguer les espèces les unes des autres.
Utilisation du jeu de données

Utilisé à l'origine comme exemple pour l'application de l'analyse linéaire discriminante de Fisher, ce jeu de données est devenu un cas typique pour de nombreuses techniques de classification automatique en apprentissage automatique (machine learning) tel que les machines à vecteurs de support (SVM).
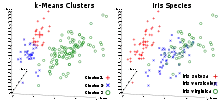
L'utilisation de cet ensemble de données dans l'analyse est cependant rare, puisqu'il ne contient que deux clusters avec une séparation plutôt évidente. L'un des groupes contient l'Iris setosa, tandis que l'autre groupe contient à la fois l'Iris virginica et l'Iris versicolor; ce dernier groupe n'étant pas séparable sans information sur l’espèce que Fisher a utilisée. Cela fait de ce jeu de données un bon exemple pour expliquer la différence entre apprentissage supervisé et apprentissage non supervisé en fouille de données (data mining) : le modèle d'analyse discriminante linéaire de Fisher ne peut être obtenu que lorsque les espèces sont connues : les étiquettes de classe et les classes ne sont pas nécessairement les mêmes[5].
Néanmoins, les trois espèces d'iris sont séparables dans une projection avec une analyse en composantes principales non linéaire[6]. Le jeu de données est approximé par l'arbre le plus proche sous certaines contraintes. On a alors construit ce que l'on appelle une metro map[4]. Les données sont projetées sur le nœud le plus proche. À chaque nœud, la répartition des points projetés est représentée par un diagramme circulaire où la surface du cercle est proportionnelle au nombre de points projetés. Il ressort du diagramme que la majorité absolue des échantillons des différentes espèces d'iris appartient à des nœuds différents. Seule une petite partie des Iris virginica est mélangée avec les Iris versicolor (les nœuds à la fois bleus et verts sur le diagramme). Par conséquent, les trois espèces d'iris (Iris setosa, Iris virginica et Iris versicolor) sont séparables grâce à une analyse en composantes principales non linéaire. Pour les distinguer, il suffit simplement de sélectionner les nœuds correspondant sur l'arbre principal.
Le jeu de données



| longueur des sépales (en cm) (Sepal length) |
largeur des sépales (en cm) (Sepal width) |
longueur des pétales (en cm) (Petal length) |
largeur des pétales (en cm) (Petal width) |
Espèce (Species) |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | I. setosa |
| 4.9 | 3.0 | 1.4 | 0.2 | I. setosa |
| 4.7 | 3.2 | 1.3 | 0.2 | I. setosa |
| 4.6 | 3.1 | 1.5 | 0.2 | I. setosa |
| 5.0 | 3.6 | 1.4 | 0.2 | I. setosa |
| 5.4 | 3.9 | 1.7 | 0.4 | I. setosa |
| 4.6 | 3.4 | 1.4 | 0.3 | I. setosa |
| 5.0 | 3.4 | 1.5 | 0.2 | I. setosa |
| 4.4 | 2.9 | 1.4 | 0.2 | I. setosa |
| 4.9 | 3.1 | 1.5 | 0.1 | I. setosa |
| 5.4 | 3.7 | 1.5 | 0.2 | I. setosa |
| 4.8 | 3.4 | 1.6 | 0.2 | I. setosa |
| 4.8 | 3.0 | 1.4 | 0.1 | I. setosa |
| 4.3 | 3.0 | 1.1 | 0.1 | I. setosa |
| 5.8 | 4.0 | 1.2 | 0.2 | I. setosa |
| 5.7 | 4.4 | 1.5 | 0.4 | I. setosa |
| 5.4 | 3.9 | 1.3 | 0.4 | I. setosa |
| 5.1 | 3.5 | 1.4 | 0.3 | I. setosa |
| 5.7 | 3.8 | 1.7 | 0.3 | I. setosa |
| 5.1 | 3.8 | 1.5 | 0.3 | I. setosa |
| 5.4 | 3.4 | 1.7 | 0.2 | I. setosa |
| 5.1 | 3.7 | 1.5 | 0.4 | I. setosa |
| 4.6 | 3.6 | 1.0 | 0.2 | I. setosa |
| 5.1 | 3.3 | 1.7 | 0.5 | I. setosa |
| 4.8 | 3.4 | 1.9 | 0.2 | I. setosa |
| 5.0 | 3.0 | 1.6 | 0.2 | I. setosa |
| 5.0 | 3.4 | 1.6 | 0.4 | I. setosa |
| 5.2 | 3.5 | 1.5 | 0.2 | I. setosa |
| 5.2 | 3.4 | 1.4 | 0.2 | I. setosa |
| 4.7 | 3.2 | 1.6 | 0.2 | I. setosa |
| 4.8 | 3.1 | 1.6 | 0.2 | I. setosa |
| 5.4 | 3.4 | 1.5 | 0.4 | I. setosa |
| 5.2 | 4.1 | 1.5 | 0.1 | I. setosa |
| 5.5 | 4.2 | 1.4 | 0.2 | I. setosa |
| 4.9 | 3.1 | 1.5 | 0.2 | I. setosa |
| 5.0 | 3.2 | 1.2 | 0.2 | I. setosa |
| 5.5 | 3.5 | 1.3 | 0.2 | I. setosa |
| 4.9 | 3.6 | 1.4 | 0.1 | I. setosa |
| 4.4 | 3.0 | 1.3 | 0.2 | I. setosa |
| 5.1 | 3.4 | 1.5 | 0.2 | I. setosa |
| 5.0 | 3.5 | 1.3 | 0.3 | I. setosa |
| 4.5 | 2.3 | 1.3 | 0.3 | I. setosa |
| 4.4 | 3.2 | 1.3 | 0.2 | I. setosa |
| 5.0 | 3.5 | 1.6 | 0.6 | I. setosa |
| 5.1 | 3.8 | 1.9 | 0.4 | I. setosa |
| 4.8 | 3.0 | 1.4 | 0.3 | I. setosa |
| 5.1 | 3.8 | 1.6 | 0.2 | I. setosa |
| 4.6 | 3.2 | 1.4 | 0.2 | I. setosa |
| 5.3 | 3.7 | 1.5 | 0.2 | I. setosa |
| 5.0 | 3.3 | 1.4 | 0.2 | I. setosa |
| 7.0 | 3.2 | 4.7 | 1.4 | I. versicolor |
| 6.4 | 3.2 | 4.5 | 1.5 | I. versicolor |
| 6.9 | 3.1 | 4.9 | 1.5 | I. versicolor |
| 5.5 | 2.3 | 4.0 | 1.3 | I. versicolor |
| 6.5 | 2.8 | 4.6 | 1.5 | I. versicolor |
| 5.7 | 2.8 | 4.5 | 1.3 | I. versicolor |
| 6.3 | 3.3 | 4.7 | 1.6 | I. versicolor |
| 4.9 | 2.4 | 3.3 | 1.0 | I. versicolor |
| 6.6 | 2.9 | 4.6 | 1.3 | I. versicolor |
| 5.2 | 2.7 | 3.9 | 1.4 | I. versicolor |
| 5.0 | 2.0 | 3.5 | 1.0 | I. versicolor |
| 5.9 | 3.0 | 4.2 | 1.5 | I. versicolor |
| 6.0 | 2.2 | 4.0 | 1.0 | I. versicolor |
| 6.1 | 2.9 | 4.7 | 1.4 | I. versicolor |
| 5.6 | 2.9 | 3.6 | 1.3 | I. versicolor |
| 6.7 | 3.1 | 4.4 | 1.4 | I. versicolor |
| 5.6 | 3.0 | 4.5 | 1.5 | I. versicolor |
| 5.8 | 2.7 | 4.1 | 1.0 | I. versicolor |
| 6.2 | 2.2 | 4.5 | 1.5 | I. versicolor |
| 5.6 | 2.5 | 3.9 | 1.1 | I. versicolor |
| 5.9 | 3.2 | 4.8 | 1.8 | I. versicolor |
| 6.1 | 2.8 | 4.0 | 1.3 | I. versicolor |
| 6.3 | 2.5 | 4.9 | 1.5 | I. versicolor |
| 6.1 | 2.8 | 4.7 | 1.2 | I. versicolor |
| 6.4 | 2.9 | 4.3 | 1.3 | I. versicolor |
| 6.6 | 3.0 | 4.4 | 1.4 | I. versicolor |
| 6.8 | 2.8 | 4.8 | 1.4 | I. versicolor |
| 6.7 | 3.0 | 5.0 | 1.7 | I. versicolor |
| 6.0 | 2.9 | 4.5 | 1.5 | I. versicolor |
| 5.7 | 2.6 | 3.5 | 1.0 | I. versicolor |
| 5.5 | 2.4 | 3.8 | 1.1 | I. versicolor |
| 5.5 | 2.4 | 3.7 | 1.0 | I. versicolor |
| 5.8 | 2.7 | 3.9 | 1.2 | I. versicolor |
| 6.0 | 2.7 | 5.1 | 1.6 | I. versicolor |
| 5.4 | 3.0 | 4.5 | 1.5 | I. versicolor |
| 6.0 | 3.4 | 4.5 | 1.6 | I. versicolor |
| 6.7 | 3.1 | 4.7 | 1.5 | I. versicolor |
| 6.3 | 2.3 | 4.4 | 1.3 | I. versicolor |
| 5.6 | 3.0 | 4.1 | 1.3 | I. versicolor |
| 5.5 | 2.5 | 4.0 | 1.3 | I. versicolor |
| 5.5 | 2.6 | 4.4 | 1.2 | I. versicolor |
| 6.1 | 3.0 | 4.6 | 1.4 | I. versicolor |
| 5.8 | 2.6 | 4.0 | 1.2 | I. versicolor |
| 5.0 | 2.3 | 3.3 | 1.0 | I. versicolor |
| 5.6 | 2.7 | 4.2 | 1.3 | I. versicolor |
| 5.7 | 3.0 | 4.2 | 1.2 | I. versicolor |
| 5.7 | 2.9 | 4.2 | 1.3 | I. versicolor |
| 6.2 | 2.9 | 4.3 | 1.3 | I. versicolor |
| 5.1 | 2.5 | 3.0 | 1.1 | I. versicolor |
| 5.7 | 2.8 | 4.1 | 1.3 | I. versicolor |
| 6.3 | 3.3 | 6.0 | 2.5 | I. virginica |
| 5.8 | 2.7 | 5.1 | 1.9 | I. virginica |
| 7.1 | 3.0 | 5.9 | 2.1 | I. virginica |
| 6.3 | 2.9 | 5.6 | 1.8 | I. virginica |
| 6.5 | 3.0 | 5.8 | 2.2 | I. virginica |
| 7.6 | 3.0 | 6.6 | 2.1 | I. virginica |
| 4.9 | 2.5 | 4.5 | 1.7 | I. virginica |
| 7.3 | 2.9 | 6.3 | 1.8 | I. virginica |
| 6.7 | 2.5 | 5.8 | 1.8 | I. virginica |
| 7.2 | 3.6 | 6.1 | 2.5 | I. virginica |
| 6.5 | 3.2 | 5.1 | 2.0 | I. virginica |
| 6.4 | 2.7 | 5.3 | 1.9 | I. virginica |
| 6.8 | 3.0 | 5.5 | 2.1 | I. virginica |
| 5.7 | 2.5 | 5.0 | 2.0 | I. virginica |
| 5.8 | 2.8 | 5.1 | 2.4 | I. virginica |
| 6.4 | 3.2 | 5.3 | 2.3 | I. virginica |
| 6.5 | 3.0 | 5.5 | 1.8 | I. virginica |
| 7.7 | 3.8 | 6.7 | 2.2 | I. virginica |
| 7.7 | 2.6 | 6.9 | 2.3 | I. virginica |
| 6.0 | 2.2 | 5.0 | 1.5 | I. virginica |
| 6.9 | 3.2 | 5.7 | 2.3 | I. virginica |
| 5.6 | 2.8 | 4.9 | 2.0 | I. virginica |
| 7.7 | 2.8 | 6.7 | 2.0 | I. virginica |
| 6.3 | 2.7 | 4.9 | 1.8 | I. virginica |
| 6.7 | 3.3 | 5.7 | 2.1 | I. virginica |
| 7.2 | 3.2 | 6.0 | 1.8 | I. virginica |
| 6.2 | 2.8 | 4.8 | 1.8 | I. virginica |
| 6.1 | 3.0 | 4.9 | 1.8 | I. virginica |
| 6.4 | 2.8 | 5.6 | 2.1 | I. virginica |
| 7.2 | 3.0 | 5.8 | 1.6 | I. virginica |
| 7.4 | 2.8 | 6.1 | 1.9 | I. virginica |
| 7.9 | 3.8 | 6.4 | 2.0 | I. virginica |
| 6.4 | 2.8 | 5.6 | 2.2 | I. virginica |
| 6.3 | 2.8 | 5.1 | 1.5 | I. virginica |
| 6.1 | 2.6 | 5.6 | 1.4 | I. virginica |
| 7.7 | 3.0 | 6.1 | 2.3 | I. virginica |
| 6.3 | 3.4 | 5.6 | 2.4 | I. virginica |
| 6.4 | 3.1 | 5.5 | 1.8 | I. virginica |
| 6.0 | 3.0 | 4.8 | 1.8 | I. virginica |
| 6.9 | 3.1 | 5.4 | 2.1 | I. virginica |
| 6.7 | 3.1 | 5.6 | 2.4 | I. virginica |
| 6.9 | 3.1 | 5.1 | 2.3 | I. virginica |
| 5.8 | 2.7 | 5.1 | 1.9 | I. virginica |
| 6.8 | 3.2 | 5.9 | 2.3 | I. virginica |
| 6.7 | 3.3 | 5.7 | 2.5 | I. virginica |
| 6.7 | 3.0 | 5.2 | 2.3 | I. virginica |
| 6.3 | 2.5 | 5.0 | 1.9 | I. virginica |
| 6.5 | 3.0 | 5.2 | 2.0 | I. virginica |
| 6.2 | 3.4 | 5.4 | 2.3 | I. virginica |
| 5.9 | 3.0 | 5.1 | 1.8 | I. virginica |
Plusieurs versions du jeu de données ont été publiées[7].
Références
- R. A. Fisher (1936).
- Edgar Anderson (1936).
- Edgar Anderson (1935).
- A. N. Gorban, A. Zinovyev.
- Ines Färber, Stephan Günnemann, Hans-Peter Kriegel, Peer Kröger, Emmanuel Müller, Erich Schubert, Thomas Seidl, Arthur Zimek (2010).
- A.N. Gorban, N.R. Sumner, and A.Y. Zinovyev, Topological grammars for data approximation, Applied Mathematics Letters Volume 20, Issue 4 (2007), 382-386.
- Bezdek, J.C. and Keller, J.M. and Krishnapuram, R. and Kuncheva, L.I. and Pal, N.R. (1999).
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Iris_flower_data_set » (voir la liste des auteurs).
Liens externes
- "Fisher's Iris Data". (Contains two errors which are documented). UCI Machine Learning Repository: Iris Data Set.
- Portail des probabilités et de la statistique
- Portail de la botanique
- Portail des données
