Kunstweg de Jost Bürgi
Le Kunstweg[1] ou Artificium de Jost Bürgi est un algorithme itératif qui permet de calculer, pour un entier positif , des valeurs approchées rationnelles des sinus des fractions pour tous les entiers , et avec une précision arbitraire préalablement fixée. Cet algorithme ne fait appel qu’à des opérations algébriques simples (additions et divisions) et fournit, pour un entier donné, les sinus de tous les simultanément.
Son inventeur est Jost Bürgi (1552-1632), un horloger, astronome et mathématicien suisse qui a travaillé au service des landgraves de Hesse-Cassel, puis des empereurs du Saint-Empire romain germanique. Il a collaboré avec Johannes Kepler au début du XVIIe siècle. Son Kunstweg, datant de la fin des années 1580, suit une démarche originale et novatrice pour son époque. Il n’a été redécouvert qu’à partir de 2014.
.png.webp)
L'algorithme
Pour un entier donné, soit un vecteur colonne composé d'entiers positifs tels que les soient des approximations grossières des .
On calcule d'abord un vecteur colonne auxiliaire en commençant par sa dernière composante en posant ; les précédentes sont obtenues en remontant par la relation : .
On calcule ensuite un nouveau vecteur colonne par : et la relation : .
Les nombres rationnels sont alors de nouvelles approximations des , plus précises que les premières. On pourra réitérer le processus par le calcul d'un vecteur colonne auxiliaire , puis d'un nouveau vecteur etc. pour obtenir des approximations de plus en plus précises.
Le document original de Bürgi (reproduit dans la Figure 1) donne un exemple pour . Le tableau se lit de droite à gauche :
- les premières approximations se trouvent dans la colonne de droite notée
- le vecteur-colonne auxiliaire se trouve à gauche de celle-ci
- les deuxièmes approximations se trouvent dans la colonne notée et ainsi de suite.
Sur ce document original de Bürgi, les nombres sont exprimés dans le système sexagésimal, ce qui rajoute une petite difficulté à son interprétation. Les angles dont on veut calculer les sinus se trouvent dans la colonne la plus à gauche du tableau.
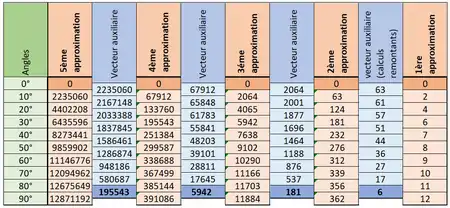
Le tableau suivant donne une traduction du manuscrit en écriture décimale (voir Figure 2).
Les valeurs fournies par la 5ème approximation de sont respectivement ; ; etc., soit en écriture décimale : ; ; etc. Pour chacune de ces valeurs, les 6 premières décimales sont correctes.
La convergence
Jost Bürgi n'a pas apporté la preuve de la convergence de son algorithme. Il faudra attendre la redécouverte du Kunstweg en 2014 pour que des mathématiciens démontrent sa convergence[2]. Pour ce faire, ils utilisent le théorème de Perron-Frobenius (1907): On considère l'application linéaire qui permet de passer d'une colonne "approximation" à la suivante. Elle est définie par la matrice carrée à coefficients positifs .
Cette matrice satisfait les conditions requises pour l'application du théorème de Perron-Frobenius. Ils montrent alors que son vecteur-propre de Frobenius est .
Ils apportent ainsi la preuve de la validité de l'algorithme de Bürgi et de sa convergence.
L'histoire du Kunstweg
La genèse
Selon ses biographes[3], Jost Bürgi ne savait pas lire le latin et il explique lui-même que, ne pouvant accéder aux écrits des maîtres, il fut amené à développer ses propres méthodes[4]. On peut se demander comment il a inventé son algorithme après en avoir constaté l'originalité.
La présentation de la progression de droite à gauche donne sans doute un indice : si l'on relit son tableau de la gauche vers la droite, il apparaît que chaque colonne est composée des différences de deux termes consécutifs de la précédente. Ainsi Bürgi a pu observer que, pour une colonne donnée, les différences secondes sont proportionnelles aux termes de la colonne initiale avec cependant une perte de précision. Il a alors pu imaginer qu'en inversant le processus, on gagnerait en précision[5]
Voici le calcul de ces différences secondes ; il faut rappeler que Bürgi était aussi l'un des promoteurs de la prostaphérèse (transformation des produits en sommes ou différences et vice-versa) :
sinus différences différences secondes (valeurs absolues)
étant constant, la proportionnalité des différences secondes avec les sinus est ainsi établie[6].
L'énigme du Kunstweg
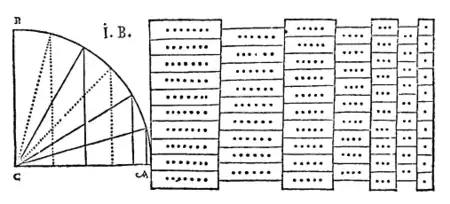
En 1588, un ami de Bürgi, Nicolaus (Ursus) Reymers publie un ouvrage, Fundamentum Astronomicum, dans lequel il fait allusion au Kunstweg de Jost Bürgi, sans en donner le détail mais uniquement un croquis accompagné d'un tableau à compléter[2].
Plus tard, lorsque Clavius lui demande des explications, Reymers ne dévoile pas la méthode de calcul sous prétexte qu'il s'est engagé auprès de Bürgi à la tenir secrète... Ce secret tiendra durant plus de 4 siècles pendant lesquels le croquis de Reymers sera considéré comme une énigme.
Il faudra attendre la découverte en 2014 du manuscrit de Bürgi dans la Bibliothèque Universitaire de Wroclaw (Breslau) pour que cette énigme soit résolue et deux ans de plus pour que l'algorithme de Bürgi soit validé par les mathématiciens.
Le Fundamentum Astronomiae
Jost Bürgi a présenté son Kunstweg dans un manuscrit jamais publié, le Fundamentum Astronomiae qu'il a remis à l'empereur Rodolphe II à la suite d'une audience en 1592. Cet ouvrage de trigonométrie comportait en outre une table des sinus développée sur 36 pages de minute en minute. On ne sait pas par quelles circonstances ce manuscrit a changé de mains pour se retrouver en 1628 à Sagan à la cour d'Albrecht von Wallenstein. Il est possible que Rodolphe II l'ait confié à Kepler qui était son mathématicien et qui fut au service de Wallenstein plus tard[7]. Le manuscrit fut déposé au Chapitre des Augustins de Sagan. Lors de la sécularisation de ce dernier en 1810, le manuscrit rejoignit le corpus de la Bibliothèque Universitaire de Wroclaw. C'est là qu'il a été redécouvert en 2014 par Menso Folkerts, historien des mathématiques.
De nos jours, Le Fundamentum Astronomiae est consultable en ligne sur le site de l'Université de Wroclaw[8].
Bibliographie
- Jost Bürgi, Fundamentum Astronomiae, Blbliotheka Uniwersyteka Wroclaw, (lire en ligne).
- Menso Folkerts, Dieter Launert et Andreas Thom, « Jost Bürgi's Method for Calculating Sines », Hist. Math., vol. 43, no 2, , p. 133-147 (zbMATH 1343.01011, arXiv 1510.03180).
- Fritz Staudacher, Jost Bürgi, Kepler und der Kaiser : Uhrmacher, Astronom, Mathematiker, Instrumentenbauer, Erz-Metallurgist, Zurich, NZZ Libro, , 4e éd..
- Jörg Waldvogel, « Jost Bürgi’s Artificium of 1586 in modern view, an ingenious algorithm for calculating tables of the sine function », Elemente der Mathematik), vol. 71, , p. 89-99 (lire en ligne, consulté le ).
- Grégoire Nicollier, « How Bürgi computed the sines of all integer angles simultaneousely in 1586 », Mathematische Semesterberichte, vol. 65, no 1, , p. 15-34 (DOI 10.1007/s00591-017-0209-0, lire en ligne).
- Denis Roegel, « A preliminary note on Bürgi’s computation of the sine of the first minute », Hal.inria, (HAL hal-01316358/document).
Notes et références
- Bürgi a nommé lui-même Kunstweg ou Artificium son algorithme. En allemand, Kunst signifie art dans le sens de travail bien fait et Weg chemin. Ainsi Kunstweg pourrait se traduire par démarche artistique ou démarche heuristique.
- Folkerts, Launert et Thom 2015.
- Staudacher (2018), p. 149 : « Fehlende Sprachkenntnisse als Handicap »..
- Bürgi-Kepler, Arithmetica Bürgii, page 7 : « Weil mir aus Mangel der Sprachen die Thür zu den Authoribus nit allzeit offen gestanden, wie andern, hab ich etwas mehr als etwa gelehrte und belesene, meinen eigenen Gedankhen nachhengen und neue Wege suechen müessen ».
- Waldvogel (2016).
- N.B. Au sens strict, la différence seconde est négative. Il s'agit ici d'une distance.
- Staudacher page 198.
- Fundamentum Astronomiae en ligne.
- Portail des mathématiques