Largeur de clique

La largeur de clique d'un graphe ${\displaystyle G}$ est le nombre minimum d'étiquettes nécessaires pour construire ${\displaystyle G}$ au moyen des 4 opérations suivantes :

• Création d'un nouveau sommet v d'étiquette i (noté i(v) ou ${\displaystyle \bullet _{i}}$)
• Union disjointe de deux graphes étiquetés G et H (notée ${\displaystyle G\oplus H}$)
• Jonction par une arête de chaque sommet étiqueté i à chaque sommet étiqueté j (noté η(i,j)), où ${\displaystyle i\neq j}$
• Renommage de l'étiquette i en étiquette j (notée ρ (i, j) ou ${\displaystyle \rho _{i\to j}}$).

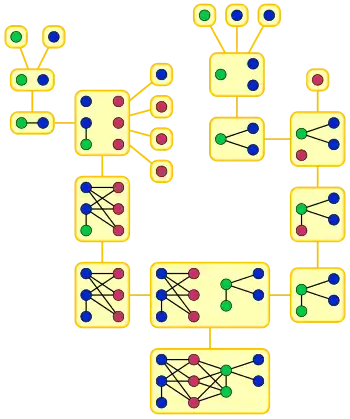
Dans l’exemple, le graphe final est obtenu par la jonction des trois sommets rouges et des deux sommets verts ; le graphe précédent est l’union disjointe des eux graphes bleu-rouge et vert-bleu, etc. La suite des graphes construits par les opérations est figurée dans l'arbre des opérations.

Les graphes de largeur de clique bornée comprennent les cographes et les graphes à distance héréditaire. Il est NP-difficile de calculer la largeur de clique lorsqu'elle n'est pas bornée, et il est inconnu si elle peut être calculée en temps polynomial lorsqu'elle est bornée ; des algorithmes d'approximation efficaces pour la largeur de clique existent. Sur la base de ces algorithmes et du théorème de Courcelle, de nombreux problèmes d'optimisation de graphes qui sont NP-difficiles pour des graphes arbitraires peuvent être résolus ou approximés rapidement sur les graphes de largeur de clique bornée.

Les séquences de construction sous-jacentes au concept de largeur de clique ont été formulées par Courcelle, Engelfriet et Rozenberg en 1990[1] et par Wanke en 1994[2]. Le nom de largeur de clique ("clique-width") a été utilisé pour un concept différent par Chlebíková en 1992[3] . Depuis 1993, le terme a son sens actuel[4].

Une suite détaillée d'opérations conduisant à un graphe de largeur de clique 3 est donnée dans la table suivante.

Arbre pour la construction de ${\displaystyle C_{6}}$

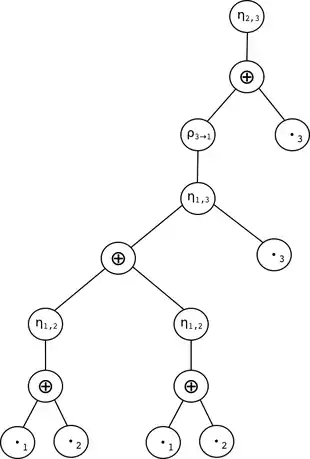
Opération	Visualisation
${\displaystyle G_{1}=\bullet _{1}}$
${\displaystyle G_{2}=\bullet _{2}}$
${\displaystyle G_{3}=G_{1}\oplus G_{2}}$
${\displaystyle G_{4}=\eta _{1,2}(G_{3})}$
${\displaystyle G_{5}=G_{4}\oplus G_{4}}$
${\displaystyle G_{6}=G_{5}\oplus \bullet _{3}}$
${\displaystyle G_{7}=\eta _{1,3}(G_{6})}$
${\displaystyle G_{8}=\rho _{3\rightarrow 1}(G_{7})}$
${\displaystyle G_{9}=G_{8}\oplus \bullet _{3}}$
${\displaystyle C_{10}=\eta _{2,3}(G_{9})}$

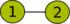
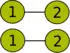
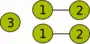
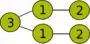
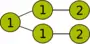
L'expression correspondante est :

${\displaystyle \eta _{2,3}(\rho _{3\rightarrow 1}(\eta _{1,3}(\eta (\bullet _{1}\oplus \bullet _{2})\oplus \eta (\bullet _{1}\oplus \bullet _{2})\oplus \bullet _{3}))\oplus \bullet _{3})}$

Les cographes sont exactement les graphes avec une largeur de clique au plus 2[5]. Chaque graphe à distance héréditaire a une largeur de clique au plus 3. La largeur de clique des graphes d'intervalles unitaires est non bornée (en fonction de leur structure de grille)[6]. De même, la largeur de clique des graphes de permutation biparti est non bornée (basée sur une structure de grille similaire)[7]. La caractérisation des cographes comme les graphes sans sous-graphe induit isomorphe à un chemin de quatre sommets sans corde permet de calculer la largeur de clique de nombreuses classes de graphes définies par des sous-graphes induits exclus.

Courcelle et Olariu en 2000[5] et Corneil et Rotics en 2005[8] ont donné les bornes suivante pour la largeur de clique de certains graphes :

• Si un graphe a une largeur de clique au plus k, alors il en est de même pour chaque sous-graphe induit du graphe[9].
• Le graphe complémentaire d'un graphe de largeur de clique k a une largeur de clique d'au plus 2k[10] .
• Les graphes de largeur arborescente w ont une largeur de clique d'au plus 3 · 2^{w − 1} . La dépendance exponentielle dans cette borne ne peut être évitée : il existe des graphes dont la largeur de clique est exponentiellement plus grande que leur largeur d'arbre[11]. Inversement, les graphes de largeur de clique bornée peuvent avoir une largeur d'arbre non bornée ; par exemple, les graphes complets à n sommets ont une largeur de clique 2 mais une largeur d'arbre n − 1 . Cependant, les graphes de largeur de clique k qui n'ont pas de graphe biparti complet K_t,t comme sous-graphe ont une largeur d'arbre d'au plus 3k(t − 1) − 1 . Par conséquent, pour toute famille de graphes creux, avoir une largeur d'arbre bornée équivaut à avoir une largeur de clique bornée[12].
• Un autre paramètre de graphes, le largeur de rang, est borné dans les deux sens par la largeur de la clique : largeur de rang ≤ largeur de la clique ≤ 2 ^{largeur de rang + 1}[13].

Par ailleurs, si un graphe G a une largeur de clique k, alors la puissance G^m a une largeur de clique d'au plus 2km^k[14]. Bien qu'il y ait un écart exponentiel des bornes entre la largeur de clique et la largeur d'arbre et la largeur de clique des puissances de graphe, ces bornes ne se combinent pas : si un graphe G a une largeur d'arbre w, alors G^m a une largeur de clique au plus égale à 2(m + 1)^{w + 1} − 2, qui est simplement exponentielle en la largeur de l'arbre[15].

De nombreux problèmes d'optimisation qui sont NP-difficiles pour des classes de graphes générales peuvent être résolus efficacement par programmation dynamique sur des graphes de largeur de clique bornée, lorsqu'une séquence de construction pour ces graphes est connue[16]^,[17]. En particulier, chaque propriété de graphe qui peut être exprimée dans la logique monadique du second ordre MSO₁ (une forme de logique permettant la quantification sur des ensembles de sommets) admet un algorithme en temps linéaire pour les graphes de largeur de clique bornée, par une des formes du théorème de Courcelle[17]. Des résultats sur les bornes pour des propriétés de classes de graphes ont été données par Bergougnoux et Kanté[18]. Des classes de graphes fermés par passage au sous-graphe induits sont présentés dans un article de synthèse de Konrad K. Dabrowski Matthew Johnson et Daniël Paulusma[19].

Des colorations de graphes optimales ou des cycles hamiltoniens pour les graphes de largeur de clique bornée se calculent en temps polynomial, lorsqu'une séquence de construction est donnée, mais l'exposant du polynôme augmente avec la largeur de clique, et les preuves de la théorie de la complexité montrent que cette dépendance est inévitable[20]. Les graphes de largeur de clique bornée ont la propriété que leur nombre chromatique est au plus une fonction de la taille de leur plus grande clique[21].

Les graphes de largeur de clique 3 peuvent être reconnus, et une séquence de construction peut être construite, en temps polynomial à l'aide d'un algorithme basé sur la décomposition fractionnée (en)[22]. Pour les graphes de largeur de clique non bornée, il est NP-difficile de calculer exactement la largeur de clique, et aussi NP-difficile d'obtenir une approximation avec une erreur additive sous-linéaire[23]. Cependant, quand la largeur de clique est bornée, il est possible d'obtenir une séquence de construction de largeur bornée (exponentiellement plus grande que la largeur de clique réelle) en temps polynomial[24]. Il est ouvert si la largeur exacte de la clique, ou une approximation plus stricte de celle-ci, peut être calculée en temps traitable à paramètres fixes, ou si elle peut être calculée en temps polynomial pour chaque borne fixe de la largeur de la clique, ou même si les graphes de largeur de clique quatre peuvent être reconnu en temps polynomial[23].

La théorie des graphes de largeur de clique bornée est similaire à celle des graphes de largeur arborescente bornée, mais contrairement à la largeur arborescente, elle s'applique aussi à des graphes denses. Si une famille de graphes a une largeur de clique bornée, alors soit elle a une largeur arborescente bornée, soit chaque graphe biparti complet est un sous-graphe d'un graphe de la famille[12]. La largeur arborescente et la largeur de clique sont également reliés par la théorie des line graphs : une famille de graphes a une largeur d'arbre bornée si et seulement si leurs line-graphs ont une largeur de clique bornée[25].

Si on note ${\displaystyle cw(G)}$ la largeur de clique et ${\displaystyle tw(G)}$ la largeur arborescente de ${\displaystyle G}$, on a l'inégalité[26] :

${\displaystyle cw(G)\leq 3\cdot 2^{tw(G)-1}}$.

On ne peut pas majorer la largeur d'arborescene par une expression en la largeur de clique, comme on peut voir sur les graphes complets : Le graphe complet ${\displaystyle K_{n}}$ a l largeur arborescente ${\displaystyle n-1}$ et une largeur de clique au plus 2. On a donc pour ${\displaystyle n\geq 4}$ :

${\displaystyle cw(K_{n})<tw(K_{n})}$.

Si ${\displaystyle G}$ n'a pas de graphe biparti complet comme sous-graphe, alors[12] :

${\displaystyle tw(G)\leq 3\cdot (n-1)\cdot cw(G)-1}$.

• (en)/(de) Cet article est partiellement ou en totalité issu des articles intitulés en anglais « Clique-width » (voir la liste des auteurs) et en allemand « Cliquenweite » (voir la liste des auteurs).

• Benjamin Bergougnoux et Mamadou Kanté, « Fast exact algorithms for some connectivity problems parameterized by clique-width », Theoretical Computer Science, vol. 782,‎ août 2019, p. 30-53 (DOI 10.1016/j.tcs.2019.02.030, lire en ligne)

• Andreas Brandstädt, F.F. Dragan, H.-O. Le et R. Mosca, « New graph classes of bounded clique-width », Theory of Computing Systems, vol. 38, n^o 5,‎ 2005, p. 623–645 (DOI 10.1007/s00224-004-1154-6, S2CID 2309695, CiteSeer^x 10.1.1.3.5994).
• Andreas Brandstädt, J. Engelfriet, H.-O. Le et V. V. Lozin, « Clique-width for 4-vertex forbidden subgraphs », Theory of Computing Systems, vol. 39, n^o 4,‎ 2006, p. 561–590 (DOI 10.1007/s00224-005-1199-1, S2CID 20050455).
• Andreas Brandstädt et Christian Hundt, « Ptolemaic graphs and interval graphs are leaf powers », Lecture Notes in Comput. Sci., Springer, Berlin, vol. 4957 « LATIN 2008: Theoretical informatics »,‎ 2008, p. 479–491 (DOI 10.1007/978-3-540-78773-0_42, Math Reviews 2472761).
• Andreas Brandstädt et V. V. Lozin, « On the linear structure and clique-width of bipartite permutation graphs », Ars Combinatoria, vol. 67,‎ 2003, p. 273–281 (CiteSeer^x 10.1.1.16.2000).
• Janka Chlebíková, « On the tree-width of a graph », Acta Mathematica Universitatis Comenianae, New Series, vol. 61, n^o 2,‎ 1992, p. 225–236 (Math Reviews 1205875, CiteSeer^x 10.1.1.30.3900).
• Olivier Cogis et Éric Thierry, « Computing maximum stable sets for distance-hereditary graphs », Discrete Optimization, vol. 2, n^o 2,‎ 2005, p. 185–188 (DOI 10.1016/j.disopt.2005.03.004, Math Reviews 2155518).
• Derek G. Corneil, Michel Habib, Jean-Marc Lanlignel, Bruce Reed et Udi Rotics, « Polynomial-time recognition of clique-width ≤ 3 graphs », Discrete Applied Mathematics, vol. 160, n^o 6,‎ 2012, p. 834–865 (DOI 10.1016/j.dam.2011.03.020, Math Reviews 2901093).
• Derek G. Corneil et Udi Rotics, « On the relationship between clique-width and treewidth (extended abstract) », Lecture Notes in Computer Science, vol. 2204 « WG 2001: Graph-Theoretic Concepts in Computer Science »,‎ 2001, p. 78–90 (DOI 10.1007/3-540-45477-2_9).
• Derek G. Corneil et Udi Rotics, « On the relationship between clique-width and treewidth », SIAM Journal on Computing, vol. 34, n^o 4,‎ 2005, p. 825–847 (DOI 10.1137/S0097539701385351, Math Reviews 2148860).
• Bruno Courcelle, Joost Engelfriet et Grzegorz Rozenberg, « Handle-rewriting hypergraph grammars », Journal of Computer and System Sciences, vol. 46, n^o 2,‎ 1993, p. 218–270 (DOI 10.1016/0022-0000(93)90004-G, Math Reviews 1217156). — Une version préliminaire a été présentée à Graph grammars and their application to computer science (Brème, 1990), lien Math Reviews.
• Bruno Courcelle, « Monadic second-order logic and hypergraph orientation », Proceedings of Eighth Annual IEEE Symposium on Logic in Computer Science (LICS '93),‎ 1993, p. 179–190 (DOI 10.1109/LICS.1993.287589, S2CID 39254668).
• Bruno Courcelle, Johann A. Makowsky et Udi Rotics, « Linear time solvable optimization problems on graphs on bounded clique width », Theory of Computing Systems, vol. 33, n^o 2,‎ 2000, p. 125–150 (DOI 10.1007/s002249910009, S2CID 15402031, CiteSeer^x 10.1.1.414.1845).
• Bruno Courcelle et S. Olariu, « Upper bounds to the clique width of graphs », Discrete Applied Mathematics, vol. 101, n^os 1–3,‎ 2000, p. 77–144 (DOI 10.1016/S0166-218X(99)00184-5, lire en ligne).
• Konrad K. Dabrowski, Matthew Johnson et Daniël Paulusma, « Clique-Width for Hereditary Graph Classes », dans Allan Lo, Richard Mycrof, Guillem Perarnau et Andrew Treglown (éditeurs), Survey in Combinatorics 2019, Cambridge University Press, coll. « London Mathematical Society Lecture Notes Series 456 », 2019 (ISBN 978-1-108-74072-2, arXiv 1901.00335), p. 1-56
• Zdeněk Dvořák et Daniel Král', « Classes of graphs with small rank decompositions are χ-bounded », Electronic Journal of Combinatorics, vol. 33, n^o 4,‎ 2012, p. 679–683 (DOI 10.1016/j.ejc.2011.12.005, arXiv 1107.2161, S2CID 5530520)
• Michael R. Fellows, Frances A. Rosamond, Udi Rotics et Stefan Szeider, « Clique-width is NP-complete », SIAM Journal on Discrete Mathematics, vol. 23, n^o 2,‎ 2009, p. 909–939 (DOI 10.1137/070687256, Math Reviews 2519936).
• Fedor V. Fomin, Petr A. Golovach, Daniel Lokshtanov et Saket Saurabh, « Intractability of clique-width parameterizations », SIAM Journal on Computing, vol. 39, n^o 5,‎ 2010, p. 1941–1956 (DOI 10.1137/080742270, Math Reviews 2592039, CiteSeer^x 10.1.1.220.1712).
• Martin Charles Golumbic et Udi Rotics, « On the clique-width of some perfect graph classes », International Journal of Foundations of Computer Science, vol. 11, n^o 3,‎ 2000, p. 423–443 (DOI 10.1142/S0129054100000260, Math Reviews 1792124).
• Frank Gurski et Egon Wanke, « The tree-width of clique-width bounded graphs without K_n,n », dans Ulrik Brandes et Dorothea Wagner (éditeurs), Graph-Theoretic Concepts in Computer Science: 26th International Workshop, WG 2000, Konstanz, Germany, June 15–17, 2000, Proceedings, Berlin, Springer, coll. « Lecture Notes in Computer Science » (n^o 1928), 2000 (DOI 10.1007/3-540-40064-8_19, Math Reviews 1850348), p. 196–205.
• Frank Gurski et Egon Wanke, « Line graphs of bounded clique-width », Discrete Mathematics, vol. 307, n^o 22,‎ 2007, p. 2734–2754 (DOI 10.1016/j.disc.2007.01.020).
• Frank Gurski et Egon Wanke, « The NLC-width and clique-width for powers of graphs of bounded tree-width », Discrete Applied Mathematics, vol. 157, n^o 4,‎ 2009, p. 583–595 (DOI 10.1016/j.dam.2008.08.031, Math Reviews 2499471).
• Petr Hliněný et Sang-il Oum, « Finding branch-decompositions and rank-decompositions », SIAM Journal on Computing, vol. 38, n^o 3,‎ 2008, p. 1012–1032 (DOI 10.1137/070685920, Math Reviews 2421076, CiteSeer^x 10.1.1.94.2272).
• Sang-il Oum et Paul Seymour, « Approximating clique-width and branch-width », Journal of Combinatorial Theory, Series B, vol. 96, n^o 4,‎ 2006, p. 514–528 (DOI 10.1016/j.jctb.2005.10.006, Math Reviews 2232389).
• Sang-il Oum, « Approximating rank-width and clique-width quickly », ACM Transactions on Algorithms, n^o 1,‎ 2009, Art. 10, 20 (DOI 10.1007/11604686_5, Math Reviews 2479181).
• Ioan Todinca, « Coloring powers of graphs of bounded clique-width », Lecture Notes in Comput. Sci., Springer, Berlin, vol. 2880 « Graph-theoretic concepts in computer science »,‎ 2003, p. 370–382 (DOI 10.1007/978-3-540-39890-5_32, Math Reviews 2080095).
• Egon Wanke, « k-NLC graphs and polynomial algorithms », Discrete Applied Mathematics, vol. 54, n^os 2–3,‎ 1994, p. 251–266 (DOI 10.1016/0166-218X(94)90026-4, Math Reviews 1300250).

• Portail des mathématiques
• Portail de l'informatique théorique