Principe des tiroirs

En mathématiques, le principe des tiroirs de Dirichlet, affirme que si n chaussettes occupent m tiroirs, et si n > m, alors au moins un tiroir doit contenir strictement plus d'une chaussette. Une autre formulation serait que m tiroirs ne peuvent contenir strictement plus de m chaussettes avec une seule chaussette par tiroir ; ajouter une autre chaussette obligera à réutiliser l'un des tiroirs.

Mathématiquement, le principe des tiroirs peut s'énoncer ainsi :

Si E et F sont deux ensembles finis tels que card(E) > card(F) et si f : E → F est une application de E dans F, alors il existe un élément de F qui admet au moins deux antécédents par f ; autrement dit il n'existe pas d'application injective de E dans F.

Appellation

La première version du principe fut énoncée par Dirichlet en 1834 sous le nom de Schubfachprinzip (« principe du tiroir ») ; sa première utilisation lui est cependant antérieure d'au moins deux siècles[1]^,[note 1]. Dans certains pays comme la Russie, ce principe s'appelle le principe de Dirichlet (à ne pas confondre avec le principe du maximum pour les fonctions harmoniques portant le même nom). Ce principe est aussi appelé principe des tiroirs de Dirichlet-Schläfli.

En anglais, ce principe est appelé pigeonhole principle. Il fait référence à la répartition des pigeons dans les cases (ou « boulins ») d'un pigeonnier[note 2].

Généralisations

Une version généralisée de ce principe déclare que, si n objets discrets occupent m récipients, alors au moins un récipient doit contenir au moins $\left\lceil {\frac {n}{m}}\right\rceil$ objets où $\lceil \ \rceil$ est la fonction partie entière par excès, qui associe à un réel x le plus petit entier supérieur ou égal à x ; ce nombre peut s'écrire avec la fonction partie entière : $\left\lceil {\frac {n}{m}}\right\rceil =-E\left(-{\frac {n}{m}}\right)$ .

Le principe des tiroirs est un exemple d'argument de dénombrement. Ce principe peut être appliqué à de nombreux problèmes sérieux, y compris ceux qui impliquent des ensembles infinis qui ne peuvent pas être mis en correspondance univoque. En approximation diophantienne, l'application quantitative du principe montre l'existence de solutions entières d'un système d'équations linéaires, résultat qui porte le nom de lemme de Siegel.

Des généralisations aux ensembles infinis existent ; ainsi, une partition d'un ensemble de cardinal α en β sous-ensembles, avec β<α, contient au moins un sous-ensemble de cardinal α si α est un cardinal régulier (en admettant l'axiome du choix).

Preuve en logique propositionnelle

On considère un nombre entier $n$ . Dire que lorsque l'on répartit $n+1$ pigeons dans $n$ trous, un trou au moins comprend 2 pigeons, c'est affirmer la négation de la proposition « il existe une répartition de $n+1$ pigeons dans $n$ trous telle que chaque trou contienne au plus un seul pigeon ».

Or on peut montrer que toutes les preuves par réfutations en résolution de la formule propositionnelle qui dit « il y a $n+1$ pigeons dans $n$ trous et au plus un pigeon par trou » est asymptotiquement de taille au moins $\textstyle {2^{\frac {n}{20}}}$ , c'est-à-dire que la taille minimale d'une preuve de cette proposition croît exponentiellement avec le nombre $n$ de trous[3].

Exemple

On considère le cas où $n=3$ , c'est-à-dire que l'on essaie de ranger 4 pigeons dans 3 trous. Pour tout $p\in \{1,2,3,4\}$ et tout $t\in \{1,2,3\}$ on définit la variable booléenne $x_{p}^{t}$ qui vaut ${\mathtt {Vrai}}$ si le pigeon numéro $p$ est dans le trou numéro $t$ et qui vaut ${\mathtt {Faux}}$ sinon.

Expression du rangement des pigeons

Soit $p\in \{1,2,3,4\}$ . On écrit que le pigeon numéro $p$ est dans l'un des trois trous par la formule logique :

x_{p}^{1}\vee x_{p}^{2}\vee x_{p}^{3}

Le fait que chacun des quatre pigeons soit dans un des trous s'écrit donc :

(x_{1}^{1}\vee x_{1}^{2}\vee x_{1}^{3})\wedge (x_{2}^{1}\vee x_{2}^{2}\vee x_{2}^{3})\wedge (x_{3}^{1}\vee x_{3}^{2}\vee x_{3}^{3})\wedge (x_{4}^{1}\vee x_{4}^{2}\vee x_{4}^{3})

Expression de ce qu'aucun trou ne contient plus d'un pigeon

Soit $t\in \{1,2,3\}$ . On écrit que le trou numéro $t$ contient au plus un pigeon, c'est-à-dire qu'il contient soit 0 pigeon, soit un seul des pigeons numérotés de 1 à 4 :

(\lnot x_{1}^{t}\wedge \lnot x_{2}^{t}\wedge \lnot x_{3}^{t}\wedge \lnot x_{4}^{t})\vee (x_{1}^{t}\wedge \lnot x_{2}^{t}\wedge \lnot x_{3}^{t}\wedge \lnot x_{4}^{t})\vee (\lnot x_{1}^{t}\wedge x_{2}^{t}\wedge \lnot x_{3}^{t}\wedge \lnot x_{4}^{t})\vee (\lnot x_{1}^{t}\wedge \lnot x_{2}^{t}\wedge x_{3}^{t}\wedge \lnot x_{4}^{t})\vee (\lnot x_{1}^{t}\wedge \lnot x_{2}^{t}\wedge \lnot x_{3}^{t}\wedge x_{4}^{t})

Formule logique résultante

La proposition « il existe une répartition de 4 pigeons dans 3 trous telle que chaque pigeon soit dans un trou et telle que chaque trou contienne au plus un seul pigeon » s'écrit donc sous la forme de la conjonction de clauses suivante :

(x_{1}^{1}\vee x_{1}^{2}\vee x_{1}^{3})\wedge (x_{2}^{1}\vee x_{2}^{2}\vee x_{2}^{3})\wedge (x_{3}^{1}\vee x_{3}^{2}\vee x_{3}^{3})\wedge (x_{4}^{1}\vee x_{4}^{2}\vee x_{4}^{3})

\bigwedge [(\lnot x_{1}^{1}\wedge \lnot x_{2}^{1}\wedge \lnot x_{3}^{1}\wedge \lnot x_{4}^{1})\vee (x_{1}^{1}\wedge \lnot x_{2}^{1}\wedge \lnot x_{3}^{1}\wedge \lnot x_{4}^{1})\vee (\lnot x_{1}^{1}\wedge x_{2}^{1}\wedge \lnot x_{3}^{1}\wedge \lnot x_{4}^{1})\vee (\lnot x_{1}^{1}\wedge \lnot x_{2}^{1}\wedge x_{3}^{1}\wedge \lnot x_{4}^{1})\vee (\lnot x_{1}^{1}\wedge \lnot x_{2}^{1}\wedge \lnot x_{3}^{1}\wedge x_{4}^{1})]

\bigwedge [(\lnot x_{1}^{2}\wedge \lnot x_{2}^{2}\wedge \lnot x_{3}^{2}\wedge \lnot x_{4}^{2})\vee (x_{1}^{2}\wedge \lnot x_{2}^{2}\wedge \lnot x_{3}^{2}\wedge \lnot x_{4}^{2})\vee (\lnot x_{1}^{2}\wedge x_{2}^{2}\wedge \lnot x_{3}^{2}\wedge \lnot x_{4}^{2})\vee (\lnot x_{1}^{2}\wedge \lnot x_{2}^{2}\wedge x_{3}^{2}\wedge \lnot x_{4}^{2})\vee (\lnot x_{1}^{2}\wedge \lnot x_{2}^{2}\wedge \lnot x_{3}^{2}\wedge x_{4}^{2})]

\bigwedge [(\lnot x_{1}^{3}\wedge \lnot x_{2}^{3}\wedge \lnot x_{3}^{3}\wedge \lnot x_{4}^{3})\vee (x_{1}^{3}\wedge \lnot x_{2}^{3}\wedge \lnot x_{3}^{3}\wedge \lnot x_{4}^{3})\vee (\lnot x_{1}^{3}\wedge x_{2}^{3}\wedge \lnot x_{3}^{3}\wedge \lnot x_{4}^{3})\vee (\lnot x_{1}^{3}\wedge \lnot x_{2}^{3}\wedge x_{3}^{3}\wedge \lnot x_{4}^{3})\vee (\lnot x_{1}^{3}\wedge \lnot x_{2}^{3}\wedge \lnot x_{3}^{3}\wedge x_{4}^{3})]

Taille de la preuve de réfutation

On cherche à montrer que la formule logique précédente est fausse. Pour cela il faut montrer qu'aucune des $2^{12}=4096$ instanciations des 12 variables $x_{1}^{1},x_{1}^{2},x_{1}^{3},x_{2}^{1},x_{2}^{2},x_{2}^{3},x_{3}^{1},x_{3}^{2},x_{3}^{3},x_{4}^{1},x_{4}^{2},x_{4}^{3}$ ne satisfait la formule. D'un point de vue informel, le théorème affirme qu'il n'existe pas de moyen « court » de montrer cela.

Applications

Bien que le principe des tiroirs semble être une observation triviale, il peut être employé de manière inattendue pour démontrer des résultats complexes.

En dehors du champ des sciences

Il est certain qu'au moins deux personnes en Australie ont exactement le même nombre de cheveux sur leur tête. En effet il est raisonnable de supposer que personne n'a plus de 6 000 000 cheveux sur la tête (une tête normale a environ 150 000 cheveux). Or l'Australie compte plus de 24 000 000 habitants. Si nous associons à chaque nombre de cheveux sur une tête un tiroir, et si nous plaçons chaque Australien dans le tiroir correspondant à son nombre de cheveux sur la tête, alors d'après le principe des tiroirs, il y a nécessairement au moins deux personnes ayant exactement le même nombre de cheveux sur la tête en Australie[4]. De plus comme il y a quatre fois plus d'Australiens que de tiroirs, on peut affirmer qu'il existe au moins quatre Australiens ayant le même nombre de cheveux[4].

Subdivisions d'un triangle

Les quatre petits triangles ont une aire égale au quart de celle du grand triangle. Si l'on choisit 9 points dans le grand triangle, alors d'après le principe des tiroirs l'un au moins des quatre petits triangles en contiendra 3.

Soit un triangle d'aire égale à 1. Si l'on choisit 9 points à l'intérieur de celui-ci, alors on peut en trouver trois d'entre eux qui déterminent un triangle d'aire inférieure à $\textstyle {\frac {1}{4}}$ . En effet on peut découper le triangle en 4 triangles d'aire quatre fois plus petite, et d'après le principe des tiroirs généralisé l'un au moins de ces petits triangles contiendra au moins trois points, délimitant une aire inférieure au quart de celle du grand triangle[5]^,[6]^,[note 3].

La méthode peut être raffinée, toujours à l'aide du principe des tiroirs, en faisant usage de ce que trois points dans un parallélogramme d'aire $\textstyle {\frac {1}{2}}$ délimitent nécessairement une aire inférieure à $\textstyle {\frac {1}{4}}$ [5]. En choisissant comme tiroirs les trois parallélogrammes formés par l'un des sommets et par le triangle des milieux (en)[note 4], il s'ensuit que parmi 7 points quelconques dans un triangle d'aire 1, on peut en trouver 3 qui délimitent un triangle d'aire $\textstyle {\frac {1}{4}}$ [5]^,[6]^,[note 3].

Sous-ensembles d'entiers de même somme

Parmi les nombres allant de 10 à 99, on en choisit dix. Il existe deux sous-ensembles disjoints ayant la même somme[4]. En effet les sommes peuvent valoir entre 10 et 855[note 5], alors qu'il y a 2¹⁰ = 1024 combinaisons possibles : on doit répartir 846 éléments dans 1022 tiroirs donc l'un des tiroirs contient deux combinaisons différentes ayant la même somme[4]^,[note 6]. Cette méthode ne permet cependant pas de trouver d'exemple de deux telles sommes[note 7].

Disposition de fous sur un échiquier

Par analogie avec le problème des huit dames, on peut se demander combien de fous au maximum on peut disposer sur un échiquier sans qu'aucun d'eux ne soit en prise si l'on ne tient pas compte de leurs couleurs.

On peut montrer en exhibant un exemple bien choisi[note 8] que la bonne réponse est supérieure ou égale à 14. Pour montrer qu'elle est également inférieure ou égale à 14, et donc égale à 14, on peut avoir recours au principe des tiroirs. Pour cela on subdivise astucieusement l'échiquier en 14 groupes de cases de telle sorte que deux fous posés sur deux cases d'un même groupe se menacent forcément : le principe des tiroirs permet alors d'affirmer qu'il est impossible de disposer 15 fous sans qu'au moins deux d'entre eux soient placés dans un même groupe et se menacent mutuellement[7].

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Disposition où aucun des 14 fous ne menace les autres.

Partage d'un échiquier en 14 tiroirs colorés dans chacun desquels deux fous se menacent forcément

Approximation d'un réel

Soient un réel $x$ et un entier $n > 0$ . Pour tout réel $y$ , on note ${y}$ sa partie fractionnaire (c'est-à-dire la différence entre $y$ et sa partie entière). Les $n + 1$ éléments $0, {x}, \dots , {n x}$ de $[0, 1[$ (non nécessairement distincts) se répartissent dans les $n$ « tiroirs » $[r / n, (r + 1)/ n [$ , où $r = 0, \dots , n - 1$ . Il existe donc un entier $r$ et deux entiers $0 \leq k < l \leq n$ tels que :

{\frac {r}{n}}\leq \{kx\},\{lx\}<{\frac {r+1}{n}}.

et donc :

|\{kx\}-\{lx\}|<{\frac {1}{n}}

.

En notant $p$ la différence des parties entières de $lx$ et $kx$ , on en déduit :

|(l-k)x-p|<{\frac {1}{n}}

,

ou encore, en introduisant l'entier $q = l - k \geq 1$ :

\left|x-{\frac {p}{q}}\right|<{\frac {1}{nq}}\leq {\frac {1}{q^{2}}}

[8]^,[note 9].

On démontre de même le théorème d'approximation de Dirichlet, un résultat plus général d'approximation simultanée de d réels. Pour d = 1, on en déduit que la mesure d'irrationalité de tout nombre irrationnel est supérieure ou égale à 2.

Problème de recherche des plus proches voisins

Le grand rectangle est découpé en 8 carrés de côté

{\frac {\delta }{2}}

. Deux points dans un de ces 8 tiroirs sont séparés de moins de

\delta

: on ne peut donc pas placer 9 points séparés de

\delta

dans le grand rectangle.

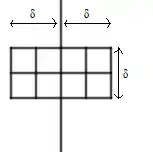
L'un des problèmes fondateurs de la géométrie algorithmique consiste à identifier parmi un ensemble de points la paire séparée par la plus petite distance. Une technique de résolution efficace repose sur la technique diviser pour régner. Celle-ci nécessite de savoir combien, dans un rectangle de longueur $2\delta$ et de largeur $\delta$ , on peut avoir de points séparés par une distance au moins égale à $\delta$ [note 10]. Par principe des tiroirs on peut montrer que ce nombre est nécessairement inférieur ou égal à 8[9].

Une paire de points les plus proches (en rouge).

Lemme de l'étoile

La preuve la plus classique du lemme de l'étoile repose essentiellement sur l'application du principe des tiroirs où chaque tiroir est un état d'un automate fini.

Fonction de hachage

Une fonction de hachage est une fonction qui transforme une suite de bits de longueur arbitraire en une chaîne de longueur fixe. Du fait qu'il y a plus de chaînes possibles en entrée qu'en sortie découle par le principe des tiroirs l'existence de collisions : plusieurs chaînes distinctes ont le même haché. Rendre ces collisions difficiles à déterminer efficacement est un enjeu important en cryptographie.

Notes et références

Notes

Le principe est notamment utilisé au XVII^e siècle par Jean Leurechon dans sa Récréation mathématique: Composée de plusieurs problèmes plaisants
Le mot pigeonhole désigne bien originellement les boulins, mais également et par analogie (depuis le 18^e siècle) les tiroirs d'un bureau[2].
En fait les deux références indiquent aussi que l'on peut montrer que cinq points suffisent (et que quatre ne suffisent pas) et donnent une généralisation pour tout polygone convexe, mais la preuve en est beaucoup plus difficile et ne fait plus appel au principe des tiroirs.
Sur l'image ci contre, il s'agit des trois parallélogrammes formés par le triangle rouge et l'un des trois triangles noirs. Le fait que leur intersection soit non-vide n'invalide pas la méthode.
En effet 855 = 91 + 92 + 93 + 94 + 95 + 96 + 97 + 98 + 99.
Il n'y a que 1022 tiroirs car on élimine la combinaison vide et la combinaison contenant tous les éléments. Les deux combinaisons obtenues peuvent ne pas être disjointes mais comme elles sont différentes il est possible de supprimer tous les éléments communs pour obtenir deux combinaisons non-vides de même somme.
Par exemple si les nombres de départ sont 15, 22, 24, 29, 31, 37, 45, 68, 76 et 90, la méthode proposée ne permet pas de trouver que 15 + 37 + 68 = 22 + 24 + 29 + 45 = 120.
Par exemple en disposant huit fous sur la rangée supérieure, et six sur la rangée inférieure, les coins étant exclus.
En affinant ce raisonnement, (en) Yann Bugeaud, Approximation by Algebraic Numbers, CUP, 2004, 292 p. (ISBN 978-0-521-82329-6, lire en ligne), p. 2, trouve deux entiers q (encore compris entre 1 et n) et p, vérifiant même : $\left|x-{\frac {p}{q}}\right|\leq {\frac {1}{(n+1)q}}$ .
On se place ici dans le cas où tous les points sont dans un même plan, mais il est possible d'utiliser des arguments analogues pour des dimensions supérieures, par exemple avec 16 sous-cubes d'arête ${\frac {\delta }{2}}$ si l'on a des points répartis dans l'espace.

Références

(en) Benoît Rittaud et Albrecht Heeffer, « The pigeonhole principle, two centuries before Dirichlet », The Mathematical Intelligencer, vol. 36, n^o 2,‎ 2014, p. 27-29 (DOI 10.1007/s00283-013-9389-1, lire en ligne).
Voir cette analyse (en) sur le site étymologique de Webster.
(en) Sanjeev Arora et Boaz Barak, Computational complexity, p. 310, Theorem 15.1
(en) [vidéo] Mathologer, The Pigeon Hole Principle: 7 gorgeous proofs sur YouTube, chapitre 1.
Jean-Paul Delahaye, Inventions mathématiques, Paris, Belin, coll. « Pour la Science », 2014, 191 p. (ISBN 978-2-84245-128-8, lire en ligne), Arts géométriques sur un plan, chap. 3 (« Non, la géométrie du triangle n'est pas morte ! »), p. 26-33.
(en) Alexander Soifer, How Does One Cut a Triangle ?, Springer, 2009 (1^re éd. 1990) (lire en ligne), chap. 7 (« Pursuit of the best result »).
Jean-Paul Delahaye, « Logique et calcul : Le principe des tiroirs », Pour la science, n^o 433,‎ janvier 2018, p. 78.
G. H. Hardy et E. M. Wright (trad. de l'anglais par François Sauvageot, préf. Catherine Goldstein), Introduction à la théorie des nombres [« An Introduction to the Theory of Numbers »] [détail de l’édition], p. 200-201.
(en) Martin Rau et Tobias Nipkow, « Verification of Closest Pair of Points Algorithms », Lecture Notes in Computer Science (en),‎ 24 juin 2020 (lire en ligne), disponible en accès libre.

Voir aussi

Articles connexes

Bibliographie

(en) Benoît Rittaud et Albrecht Heeffer, « The pigeonhole principle, two centuries before Dirichlet », The Mathematical Intelligencer, vol. 36, n^o 2,‎ 2014, p. 27-29 (DOI 10.1007/s00283-013-9389-1, lire en ligne).
Jean-Paul Delahaye, « Trivial mais puissant : le principe des tiroirs », Pour la science, vol. 483,‎ janvier 2018

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[2] Le principe est notamment utilisé au XVII^e siècle par Jean Leurechon dans sa Récréation mathématique: Composée de plusieurs problèmes plaisants

[4] Le mot pigeonhole désigne bien originellement les boulins, mais également et par analogie (depuis le 18^e siècle) les tiroirs d'un bureau[2].

[general-9] En fait les deux références indiquent aussi que l'on peut montrer que cinq points suffisent (et que quatre ne suffisent pas) et donnent une généralisation pour tout polygone convexe, mais la preuve en est beaucoup plus difficile et ne fait plus appel au principe des tiroirs.

[10] Sur l'image ci contre, il s'agit des trois parallélogrammes formés par le triangle rouge et l'un des trois triangles noirs. Le fait que leur intersection soit non-vide n'invalide pas la méthode.

[11] En effet 855 = 91 + 92 + 93 + 94 + 95 + 96 + 97 + 98 + 99.

[12] Il n'y a que 1022 tiroirs car on élimine la combinaison vide et la combinaison contenant tous les éléments. Les deux combinaisons obtenues peuvent ne pas être disjointes mais comme elles sont différentes il est possible de supprimer tous les éléments communs pour obtenir deux combinaisons non-vides de même somme.

[13] Par exemple si les nombres de départ sont 15, 22, 24, 29, 31, 37, 45, 68, 76 et 90, la méthode proposée ne permet pas de trouver que 15 + 37 + 68 = 22 + 24 + 29 + 45 = 120.

[14] Par exemple en disposant huit fous sur la rangée supérieure, et six sur la rangée inférieure, les coins étant exclus.

[17] En affinant ce raisonnement, (en) Yann Bugeaud, Approximation by Algebraic Numbers, CUP, 2004, 292 p. (ISBN 978-0-521-82329-6, lire en ligne), p. 2, trouve deux entiers q (encore compris entre 1 et n) et p, vérifiant même : $\left|x-{\frac {p}{q}}\right|\leq {\frac {1}{(n+1)q}}$ .

[18] On se place ici dans le cas où tous les points sont dans un même plan, mais il est possible d'utiliser des arguments analogues pour des dimensions supérieures, par exemple avec 16 sous-cubes d'arête ${\frac {\delta }{2}}$ si l'on a des points répartis dans l'espace.

[1] (en) Benoît Rittaud et Albrecht Heeffer, « The pigeonhole principle, two centuries before Dirichlet », The Mathematical Intelligencer, vol. 36, n^o 2,‎ 2014, p. 27-29 (DOI 10.1007/s00283-013-9389-1, lire en ligne).

[3] Voir cette analyse (en) sur le site étymologique de Webster.

[5] (en) Sanjeev Arora et Boaz Barak, Computational complexity, p. 310, Theorem 15.1

[mathologer-6] (en) [vidéo] Mathologer, The Pigeon Hole Principle: 7 gorgeous proofs sur YouTube, chapitre 1.

[delahaye-7] Jean-Paul Delahaye, Inventions mathématiques, Paris, Belin, coll. « Pour la Science », 2014, 191 p. (ISBN 978-2-84245-128-8, lire en ligne), Arts géométriques sur un plan, chap. 3 (« Non, la géométrie du triangle n'est pas morte ! »), p. 26-33.

[Soifer-8] (en) Alexander Soifer, How Does One Cut a Triangle ?, Springer, 2009 (1^re éd. 1990) (lire en ligne), chap. 7 (« Pursuit of the best result »).

[delahaye18-15] Jean-Paul Delahaye, « Logique et calcul : Le principe des tiroirs », Pour la science, n^o 433,‎ janvier 2018, p. 78.

[16] G. H. Hardy et E. M. Wright (trad. de l'anglais par François Sauvageot, préf. Catherine Goldstein), Introduction à la théorie des nombres [« An Introduction to the Theory of Numbers »] [détail de l’édition], p. 200-201.

[rau-19] (en) Martin Rau et Tobias Nipkow, « Verification of Closest Pair of Points Algorithms », Lecture Notes in Computer Science (en),‎ 24 juin 2020 (lire en ligne), disponible en accès libre.